基于飞行数据反演解算的SINS空中标定技术
2018-10-12戴邵武聂子健戴洪德陈强强
戴邵武,聂子健,戴洪德,陈强强
(海军航空大学,山东烟台264001)
随着捷联式惯导系统(Strapdown Inertial Navigation System,SINS)相较于平台式惯导系统在体积、成本及可靠性等方面的优势日益突显。目前,我国主战飞机的惯导系统逐渐由SINS所取代。然而,SINS直接“捆绑”在机体上,易受到各种外部环境的干扰,且随着工作时间的延长,导航性能将会下降,可能无法满足飞机的导航精度要求。因此,需要对SINS进行标定,以补偿相应的误差项。
我国对SINS的标定主要是基于实验室的定期拆卸标定[1],这种标定方法繁琐复杂,须要借助转台等专业测试设备才能完成对SINS的标定,不便于使用与维护。
为改进SINS的标定方法,国内外许多学者开始研究免拆卸标定方法[2-6]。陆志东等提出GPS/SINS组合导航系统空中系统级标定方法,通过设计飞机的机动动作,以激励SINS中的误差项,在一个飞行架次结束后即可完成对SINS误差的标定[7]。杨功流等提出一种弹载SINS/CNS组合导航系统免拆卸标定方法,将星敏感器安装误差扩充到系统状态向量中,设计导弹运动轨迹,对该标定方法进行了仿真验证,取得了较好的标定精度[8]。彭慧等针对高超声速飞行器进行了基于Kalman滤波的惯性器件误差标定,成功标定出标度因数误差与安装误差[9]。然而,这些标定方法均通过正向导航解算实现对SINS的标定。
本文基于GPS/SINS组合导航仿真输出的飞行数据进行反演解算,以得到惯性器件的输出增量,并结合系统级空中标定原理对机载SINS中的误差项进行标定。
1 SINS正向导航解算
1.1 SINS微分方程组
SINS微分方程组中用到的坐标系有:i为惯性坐标系;e为地球坐标系;n为导航坐标系(E-N-U);b为机体坐标系(右-前-上)。它由姿态、速度和位置微分方程组成,即[10]:

1.2 SINS导航参数更新
SINS导航参数的更新即指对姿态、速度和位置信息进行更新。
设导航参数更新周期为Tm,运用“单子样+前一周期”算法对惯性器件输出增量进行补偿[11-13]。下面分别给出各导航参数的更新过程。
1.2.1 姿态更新
由矩阵链式法则:


式(3)中:Δθm-1、Δθm分别为陀螺仪在Tm-1与Tm内的角增量。
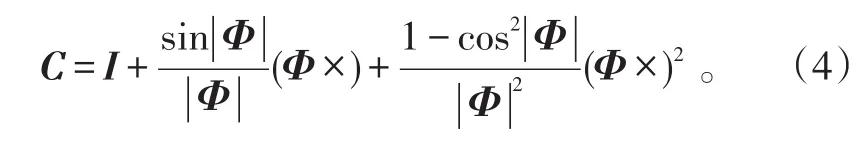
1.2.2 速度更新与位置更新
根据tm-1时刻的速度,可得出tm时刻的速度:
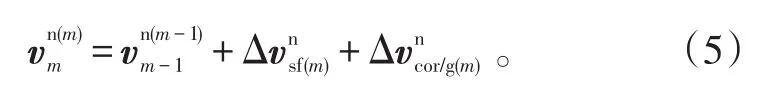

式(6)中:Δvrot,m对速度旋转误差进行补偿;Δvscull,m对划桨误差进行补偿。

式(7)~(8)中,Δvm-1、Δvm分别为加速度计在Tm-1与Tm内的速度增量。
基于速度更新,可以根据tm-1时刻的位置pm-1解算出tm时刻的位置为:
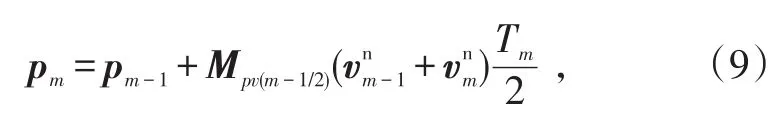
式中,Mpv(m-1/2)为tm-1/2时刻的线性外推计算值。
2 SINS反演解算
反演算法可视为SINS导航参数更新的逆过程。该算法只需根据载体的GPS/SINS组合导航输出的姿态角和位置信息,即可以实现对惯性器件输出值的仿真[14-15]。
2.1 姿态角和位置序列拟合
运用Matlab现有的spline函数即可对姿态角和位置序列拟合。对纬度序列Lm在[tm-1,tm]内进行3次样条函数拟合,可得:
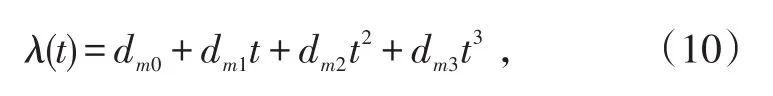
式中,dm0、dm1、dm2、dm3为纬度拟合系数。
由纬度L与SINS的北向速度之间的关系:

式中,RM,h=RM+h,取L与RM,h为Tm中间时刻tm-1/2的值。

同理,根据经度λ与东向速度、高度h与天向速度之间的关系,可得到:
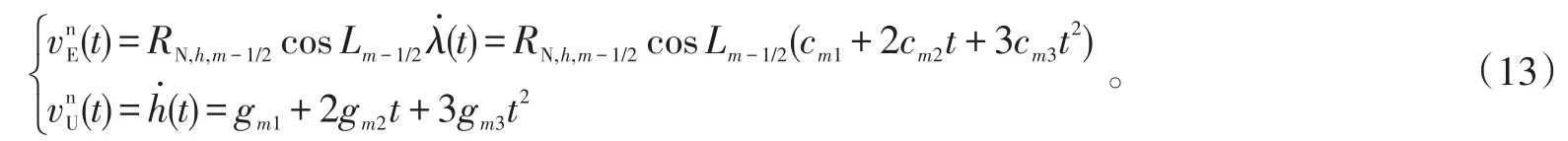
式(13)中,cm1、cm2、cm3与gm1、gm2、gm3分别为经度和高度拟合系数。
由式(10)~(13)即可得到位置函数P(t)和速度函数vn(t),同理,对姿态角进行三次样条函数拟合,可得对应的拟合函数为A(t),此处不再赘述。
2.2 惯性器件输出增量仿真
以Tk=tk-tk-1为SINS反演解算周期,对姿态角拟合函数A(t)和速度拟合函数vn(t)插值可得对应序列Ak和。
由式(2)变形得:
由于已知姿态序列Ak,即已知。可根据旋转矢量解出,其中的可根据p(t)和vn(t)插值解出。再将代入式(4)可解算出旋转矢量Φk,然后将Φk代入式(4)可逆向解算出陀螺仪的角增量输出值:
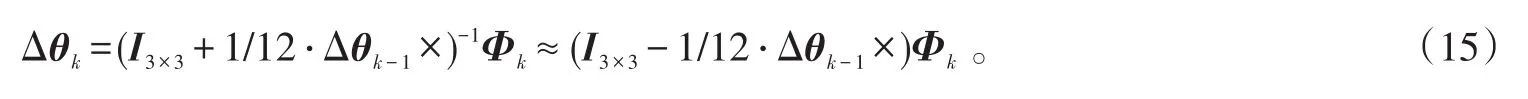
由式(5)变形得:

将式(16)进行整理,得:

式(15)和(17)即为惯性器件输出增量的仿真值。一般地,反演解算初始化设置Δθ0=0,Δv0=0。
3 SINS空中标定方案设计
3.1 标定整体思路
SINS空中标定流程见图1。具体流程为:首先,将组合导航仿真输出的姿态角、位置数据进行反演解算,以得到惯性器件的仿真输出值;然后,利用引入误差后的惯性器件输出值作为SINS的输入并进行导航解算,并以GPS和SINS输出的误差为观测量;最后,运用Kalman滤波对惯性器件误差进行系统级标定。

图1 系统级空中标定流程图Fig.1 System-level in-flight calibration flow chart
3.2 Kalman滤波器设计
3.2.1 状态方程设计
在一个标定周期内,若不进行拆装,可认为SINS的安装误差不发生变化[16]。以SINS的姿态误差、速度误差、位置误差及惯性器件的常值误差和标度因数误差作为状态向量,可得1个21维的状态方程:
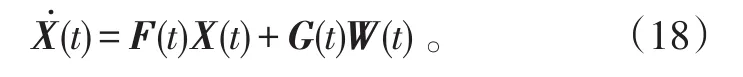
式(18)中:X(t)=[φEφNφUδvEδvNδvUδL δλδh εb,x εb,yεb,z∇a,x∇a,y∇a,zδKa,xδKa,yδKa,zδKg,xδKg,yδKg,z]T,其中,εb=[εb,xεb,yεb,z]T为陀螺仪的常值漂移,∇a=[∇a,x∇a,y∇a,z]T为加速度计的零偏误差,δKg=[δKg,xδKg,yδKg,z]T为陀螺仪标度因数误差,δKa=[δKa,xδKa,yδKa,z]T为加速度计标度因数误差;F21×21(t)为21维的系统矩阵;W(t)=[wg,xwg,ywg,zwa,xwa,ywa,z]T为3个轴向的陀螺仪与加速度计随机噪声;G(t)为噪声驱动阵。
将F(t)分为4大块,即:

式(19)中:FN(9×9)为 SINS 误差状态矩阵;矩阵FN、FM、FS中的具体参数可根据文献[17]中的SINS误差模型,去掉安装误差后获得。
3.2.2 量测方程设计
以GPS和SINS输出的误差为观测量,可得:
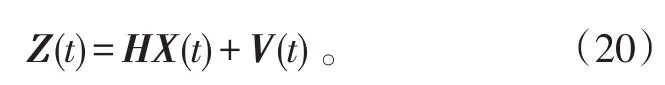
式(20)中:Z(t)为量测向量;H为量测矩阵;V(t)为观测噪声。
观测量的选取决定观测矩阵和观测噪声的形式,本文以速度误差为观测量[18],则:

对应的观测矩阵为:

4 飞行数据处理与标定仿真分析
已知SINS的3个陀螺常值漂移均为0.01(°)/h,加速度计零偏误差均为100 μg,陀螺仪与加速度计的标度因数误差均为100×10-6。原始飞行数据输出频率为1Hz,首先,通过对其进行拟合、插值,获得输出频率为100Hz的姿态序列Ak、位置序列Pk和速度序列;然后,利用这些数据序列进行SINS反演解算,以得到惯性器件输出增量信息,如图2、3所示。
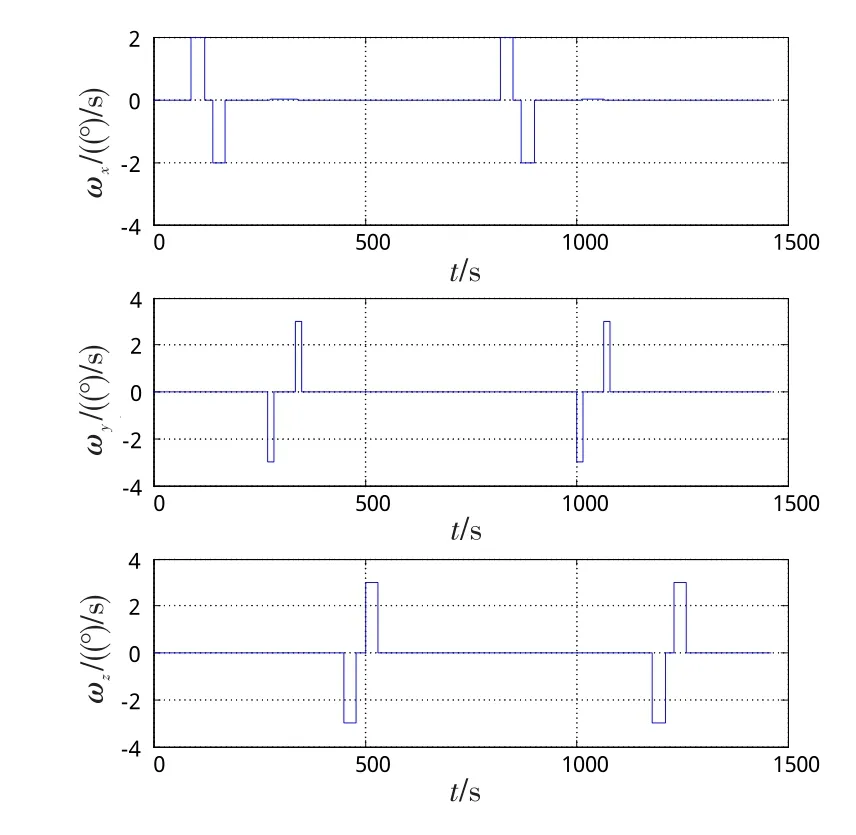
图2 陀螺仪反演输出值Fig.2 Gyro inversion output values

图3 加速度计反演输出值Fig.3 Accelerometer inversion output values
对反演解算得到的惯性器件输出增量引入误差后进行纯惯导解算,并以GPS和SINS输出的速度误差为观测量,对SINS中的陀螺仪、加速度计的常值误差和标度因数误差进行标定,得到的标定结果如图4~图7所示。

图4 陀螺仪常值漂移估计曲线Fig.4 Gyro constant bias estimation curves

图5 加速度计零偏估计Fig.5 Accelerometer constant bias estimation
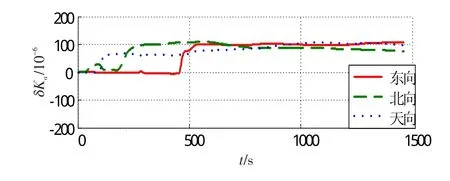
图6 加速度计标度因数误差估计Fig.6 Accelerometer scale factor error estimation
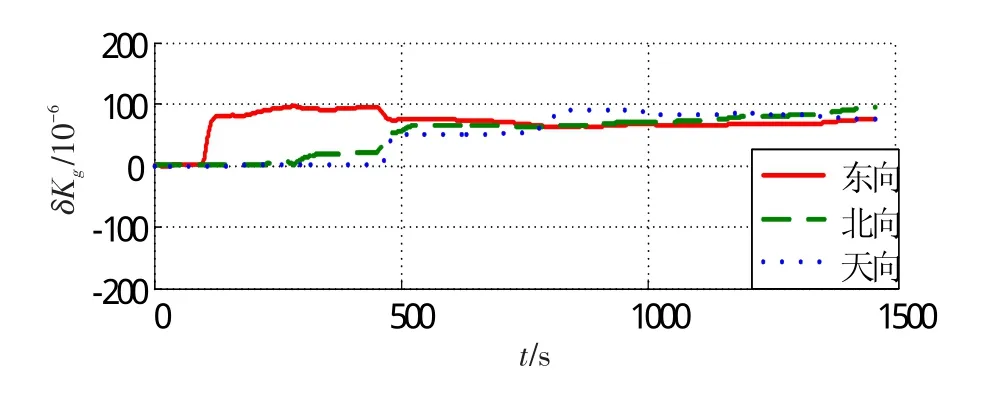
图7 陀螺仪标度因数误差估计Fig.7 Gyro scale factor error estimation
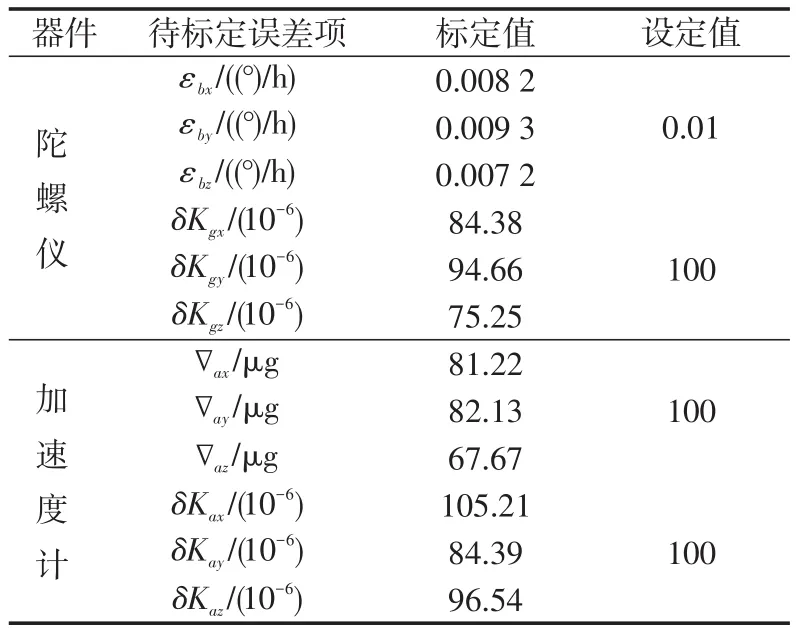
表1 以速度误差为观测量的标定结果Tab.1 Calibration results with observation of velocity errors
由图4~7可知,待标定的误差参数均能收敛到稳定值。以速度误差作为观测量时,估计天向陀螺常值漂移εb,z所用的时间最长,且估计效果较差,而其余方向的陀螺和加速度计对应的常值误差、标度因数误差均能被估计出来,具体标定结果如表1所示。
将表1的标定值与设定值对比,东向和北向陀螺常值漂移的估计精度优于0.002(°)/h,东向和北向加速度计零偏的估计精度优于20 μg,天向陀螺的标度因数误差估计精度较差,其余方向的陀螺、加速度计对应的标度因数误差估计精度均优于20×10-6。在SINS进行解算时,将惯性器件的输出值减去对应的误差估计值,即可提高SINS的导航精度。
5 结论
本文提出了一种基于飞行数据反演解算的机载SINS空中标定方法。首先,利用飞行数据反演解算得出陀螺仪和加速度计输出增量并进行纯惯导解算;然后,以速度误差为观测量,设计对应的Kalman滤波器,完成了对惯性器件误差项的估计,为机载SINS的空中标定提供了一种新途径。仿真结果表明,该标定方法可以对惯性器件的常值误差和标度因数误差进行标定,实现了SINS的免拆卸标定。同时,仿真结果也验证了该方法的可行性,应用于实际中可有效提升机载SINS的作战效能。
