太阳电池阵展开与锁定过程的多体动力学分析*
2018-10-11刘铸永时军委王检耀
刘铸永时军委 王检耀
(1.上海交通大学 船舶海洋与建筑工程学院, 上海 200240) (2.上海市空间飞行器机构重点实验室, 上海 201108)
引言
大型航天器外部通常安装多个柔性附件,如太阳帆板、天线、机械臂等[1].在航天器入轨后,太阳帆板等附件将在扭簧作用下由收拢状态展开锁定成伸展状态.这些机构的展开过程中,锁定部位会产生接触碰撞,导致机构关节处承受较大的撞击载荷,对于柔性附件的结构强度、航天器的姿态、在轨运行精度等方面均有影响.因此对于锁定撞击过程的准确预测有重要意义[2].
柔性附件的展开锁定过程是典型的变拓扑、非线性刚柔耦合多体系统动力学问题.以往对于展开动力学的研究一般将板间铰链视为理想铰[3,4],展开到位时施加与角度相关的撞击力矩模拟锁定过程.由于对板间接触碰撞过程的简化,提高了全局动力学仿真的效率,但是也影响了仿真结果尤其是碰撞力的可信性.
本文以某展开机构为研究对象,将板间铰链作为物体实际建立到动力学模型中,基于Hertz接触理论建立锁销和锁槽间的碰撞模型,实现展开锁定全过程的动力学仿真.由于Hertz接触理论中需要选取接触刚度和指数等参数,研究了碰撞参数对仿真结果的影响,给出了如何选取碰撞参数进行太阳电池阵展开与锁定动力学仿真的策略.
1 展开系统结构
1.1 系统组成
图1为某航天器太阳电池阵结构简图.系统由航天器本体(hub)、连接架(yoke)、3块太阳帆板(panel)和铰链等所组成,其中航天器本体、连接块、太阳帆板三者之间都是通过扭簧铰链相互铰接,由此形成链式结构.太阳阵释放前处于折叠状态,在航天器入轨后各展开构件靠扭簧驱动而同步展开,展开过程中各个构件之间通过绳索联动装置(CCL)保持同步性,展开到预定位置后触发锁定装置使帆板最终锁定在期望位置.

图1 展开机构Fig.1 Deployable mechanism
1.2 锁定机构
图2为板间铰链示意图,铰链两构件分别固接在相邻的两块板上,铰链之间为旋转铰.展开过程中,锁销在凸轮表面滑动,进入锁槽后实现锁定.
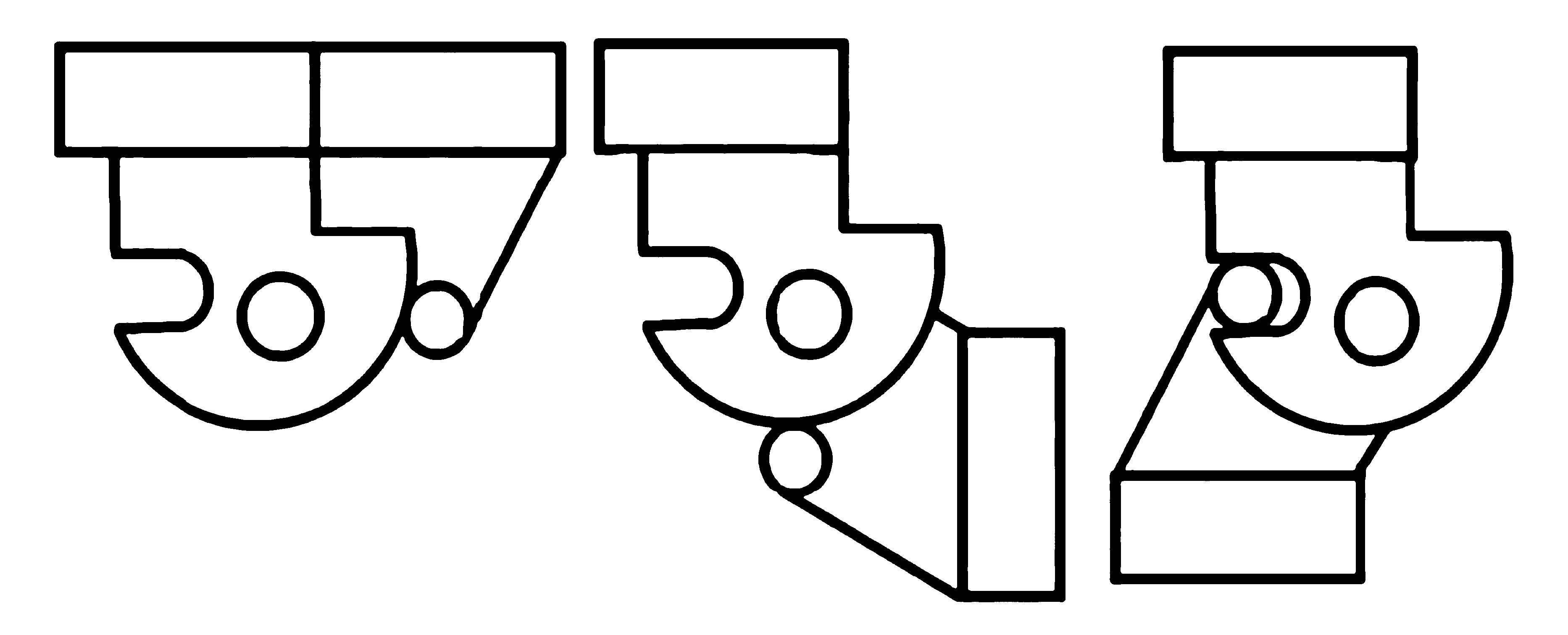
图2 锁定机构示意图Fig.2 Schematic diagram of locking mechanism
2 多体动力学建模
如图3所示, 柔性体Bi和Bj通过铰Hi连接.对柔性体用集中质量有限元离散,则柔性体Bi上任一点P的绝对位置可表示为:
(1)

图3 多体系统运动学描述Fig.3 Kinematic description of mutibody system
对式(1)分别对时间t求一次和两次导数,并加以整理,可得到绝对速度和加速度的矩阵表达式:
(2)
(3)
其中:
(4)
(5)
(6)

基于速度变分原理,单柔性体的动力学方程写为[5]:
(7)
其中m,w,fext,fint分别称为广义质量阵、广义惯性力阵、广义外力阵和广义变形力阵.
(8)
(9)
(10)
(11)
其中Ca和Ka分别为柔性体模态刚度阵和模态阻尼阵.对于单个自由的柔性体,由于广义坐标独立, 式(7)可以写为:

(12)
对于含有n个通过铰连接的物体的系统,系统的动力学方程可组集为:
(13)
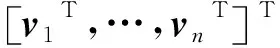
3 接触碰撞模型
接触碰撞问题的求解方法一般有三类:冲量动量法[5,6]、连续碰撞力方法[7,8]和非线性有限元方法[9,10].基于刚体假设的冲量动量法在动力学计算中只有速度和冲量项,计算效率很高,但是该方法不能计算出碰撞力的时间历程;连续碰撞力方法把碰撞看成有限时间内的接触过程,该方法考虑到接触区域的变形,在接触区域施加一个弹簧-阻尼力元来近似代替碰撞力,因此碰撞力是物体间的嵌入量和嵌入速率的函数,可以直接施加到动力学方程中求解接触碰撞的动力学过程;非线性有限元方法则是对接触作用进行精细化描述,通过将接触域离散成若干接触点对,再把接触力元或约束施加到接触点对上,该方法的精度最高,但是需要付出极高的计算代价.根据展开机构动力学仿真对效率的要求,本文采用连续碰撞力方法建立接触碰撞模型.最常用的碰撞力公式为Hertz接触理论[11]:
f=kδn
(14)

(15)

在锁销和锁槽锁定的过程中,二者有相对的滑动,必须考虑摩擦作用.因此在建模的过程中,法向接触采用Hertz模型,切向滑动采用修正的库仑摩擦模型.
4 仿真分析
由于Hertz公式中的接触刚度k只在球-球、球-平面等几种简单几何形状接触问题中有解析解.而展开机构锁定时的撞击多为不同曲率圆柱面或更一般形状之间的接触,接触刚度的选取只能依赖于经验.本文分别采用不同接触刚度和碰撞指数(见表1)下进行仿真分析,研究碰撞参数的数值对计算结果的影响.绳索联动装置(CCL)建模采用等效力元模型,仿真时所采用微分代数方程的求解方法为Gear方法.
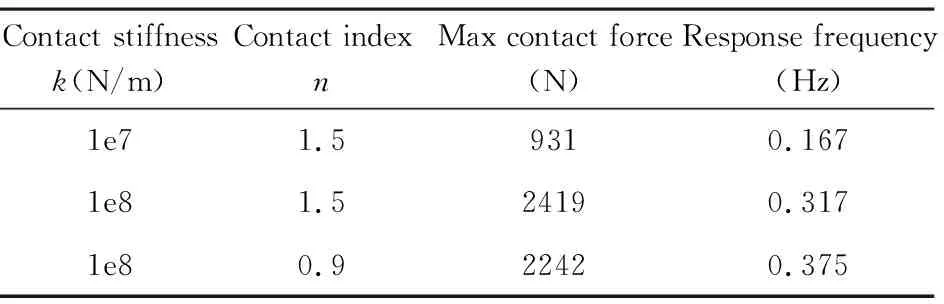
表1 不同碰撞参数下动力学响应的比较Table 1 Comparison of dynamic responses with different contact parameters
图4为根部铰链锁定后撞击力大小曲线,将不同刚度下碰撞力的峰值列于表1中.图5为外板末端中点垂直于板面的速度响应曲线,对三条曲线进行FFT分析后可以得到帆板振动的基频,同样列于表1中.
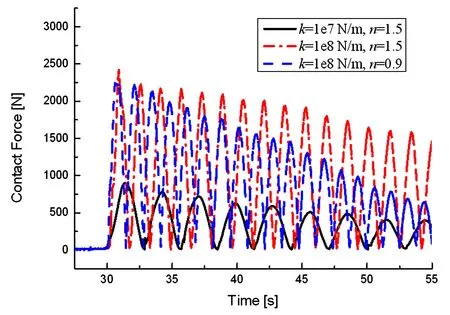
图4 根部铰链撞击力Fig.4 Contact force on the root hinge
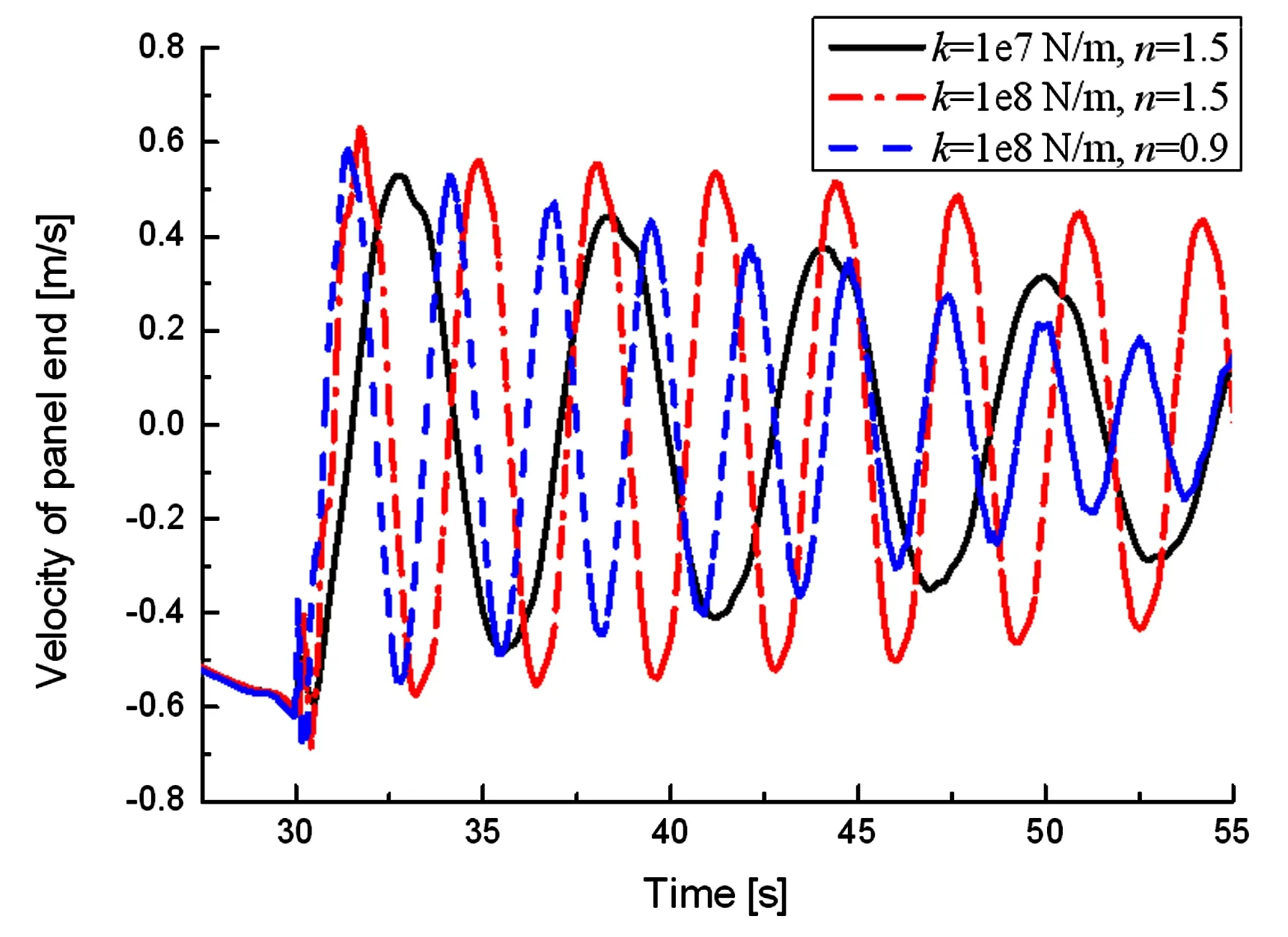
图5 外板末端中点垂直板面方向的速度Fig.5 Velocity of tip midpoint of the outer plate in the vertical direction
从表1可以看出,碰撞参数的选取不仅影响到碰撞力的大小,还会影响到系统振动的频率.因此,选取合适的碰撞参数进行撞击力的计算是尤为关键的.
5 展开锁定动力学仿真策略
图6给出了如何选取碰撞参数进行太阳电池阵动力学展开动力学仿真的策略.首先根据经验选取碰撞刚度、指数等参数,进行太阳电池阵的展开和锁定动力学仿真.然后对锁定后的动力学仿真结果进行傅里叶变换,分析其动力学响应的频率.再与太阳电池阵锁定后结构实验测得的频率进行比较.如果二者不吻合,调整接触碰撞参数,再次进行动力学仿真,直到锁定后动力学仿真频率与实验测得基频相等,此时说明仿真时所选取的碰撞参数是合理的,动力学仿真结果是可信的.

图6 展开锁定过程动力学仿真策略示意图Fig.6 Schematic diagram of dynamic simulation strategy of deployment and lockingprocess
本文所采用的算例中,实验测得锁定后太阳电池阵结构的基频为0.17Hz.由表1可得,太阳电池阵展开和锁定动力学仿真时碰撞参数应选取k=1×107N/s, 指数n=1.5.
6 结论
本文建立了柔性太阳电池阵展开机构的刚柔耦合多体系统动力学模型,将板间铰链作为实际物体处理,采用Hertz接触理论建立了锁销和锁槽之间的碰撞模型,实现了展开锁定全过程的动力学仿真.研究了不同接触刚度和指数的选取对系统动力学响应的影响,结果表明:碰撞参数的选取不仅影响到碰撞力的大小,还会影响到锁定后系统振动的频率.最后给出了如何选取碰撞参数进行太阳电池阵展开锁定动力学仿真的策略.
