Z型折叠机翼的气动力计算及非线性动力学分析*

郭翔鹰 陈璐璐 张伟

(北京工业大学 机械工程与应用电子技术学院, 北京 100124)

引言

为了满足多飞行环境(如高度、速度)要求,或执行不同任务使命(如巡航、盘旋、攻击等),人们希望飞行器形态能像鸟类一样在飞行过程中作相应的调整,达到全飞行阶段性能的优化[1]. 折叠机翼变体飞行器是人类在尝试过程中的一个重大突破,它的变形有利于提高飞机的机动性和敏捷性,提高飞机的综合性能. 同时大幅度的变形也导致飞机的转动惯量、重心位置、焦点位置等一系列机体特性的改变,飞机的气动弹性和动态稳定性也随之改变,因此需要对折叠机翼变体飞机气动特性进行深入研究.

气动弹性力学是一门涉及空气动力学、结构动力学和弹性力学的交叉学科,主要研究各类气动弹性现象[2,3]. 变体飞行器可通过机翼机身气动外形在飞行状态中的自适应变化,提高飞行器的综合性能,使飞行器在不同飞行环境状态下的气动性能均达到最佳[4]. 欧洲和美国的许多研究机构(如NASA,AFRL,DARPA等)进行了大量的对可变体飞行器气动力的研究工作[5-9]. 近年来,Emily[10]分析了蝙蝠翼的展开变形,利用蝙蝠迅速在飞行中完成180°旋转等自身特点,把形态学与飞机展开联系起来,利用升力线理论和XFOIL分析蝙蝠翅膀变身.研究表明飞行中保持机翼表面连续性的同时,通过改变翅膀的弯度和扭曲,可大大提高蝙蝠形状机翼的升力和升阻比. Samareh[11]等人研究了一种能自动生成关于气动参数、几何参数和形状变化参数的模型,此模型可以用于研究结构的大变形问题. Dowell和Tang[12]运用线性平板理论将可折叠飞行器分为机身、內翼和外翼三个部分,建立了整体结构的运动方程,运用三自由度时域涡格气动力模型研究了线性气弹稳定性,包括机翼折叠角和内、外翼铰链扭转刚度对结构动力学特性和气动弹性稳定性的影响,并与实验进行了对比. Snyder[13]研究了Martin折叠机翼的颤振,该折叠机翼可以变化200%的机翼面积. 在Nastran平台下建立了折叠翼的结构动力有限元模型,预计了不同折叠角度下机翼的固有频率和颤振速度. Jung[14]研究了机翼折叠运动中亚音速非定常气动力特性,描述了机翼每个部件在整体坐标和局部坐标中的几何关系式,结果表明折叠机翼更适合冲刺,随折叠角的增加,升力系数和风阻系数降低. Hernández[15]利用有限元方法研究了折叠板的自由振动. Brailovski[16]等人建立了一种变形机翼的流固耦合模型来评估这种变形机翼在不同飞行条件下的力学性能和气动性能. 乐挺[17]进行了机翼变形过程中的 Z 型翼变体飞机纵向多体动力学建模仿真,推导了变形过程中变体飞机的纵向动力学方程 . 结果表明,折叠过程中气动特性的变化是影响飞机动态特性的主要因素. 陈钱[18]研究了飞行器的变形方式存在三种形式:局部小变形、中等变形和大尺度变形. 对于大尺度变形在最近的大型研究项目“morphing aircraft structure”中,确立了蝙蝠翼方案和折叠翼方案,对后者进行了风洞试验. 郭秋亭[19]等人通过数值模拟指出跨声速飞行时,机翼折叠展开过程中其气动特性会发生急剧的变化. 张伟[20,21]等人设计了一种全尺寸折叠翼飞行器,并且对该飞行器不同折叠角度状态的模态和动态响应进行分析,结果表明折叠翼的折叠角度小于90°时,其第3、第4阶模态表现为弯扭组合变形,容易在亚声速条件下发生颤振现象. Wang[22,23]等对任意数量翼面的折叠翼模型的气动弹性和结构动力学做了相关研究. Murugan[24]等人以材料在飞机变形方向刚度最小,在承受气动力方向弯曲刚度最大为设计目标,设计了一种变形飞机的蒙皮. Otsuka[25]利用一种基于刚柔耦合的多体动力学方法建立了折叠机翼的动力学方程,描述了机翼折叠的弯扭耦合运动和刚体运动. 尹文强[26]等研究了飞翼布局折叠机翼变体飞机的操稳特性,自行设计飞翼布局折叠机翼变体飞机,结合工程估算法和CFD仿真分析机翼折叠过程对飞机操纵性的影响. 倪迎鸽[27,28]等根据折叠机翼的特点基于模态综合法建立了颤振分析的参数化气动弹性模型,对该模型分别采用模态价值分析方法和平衡截断降阶方法建立结构的降阶模型,并且利用可控度、可观度对两种降阶模型的精度进行了对比分析.

1 作用在Z型折叠机翼上的气动力推导

考虑亚音速气动力作用下折叠机翼结构的气动特性,所以本文选用薄翼理论计算气动力,对于理想不可压缩流体的翼型绕流,流场为势流场,势函数必满足拉普拉斯线性方程和叠加原理. 假设翼型厚度很小,故只需分布涡即可. 当中弧线的弯度很小时,在中弧线上布涡可以认为和在弦线上布涡的作用是一样的(如图1所示).

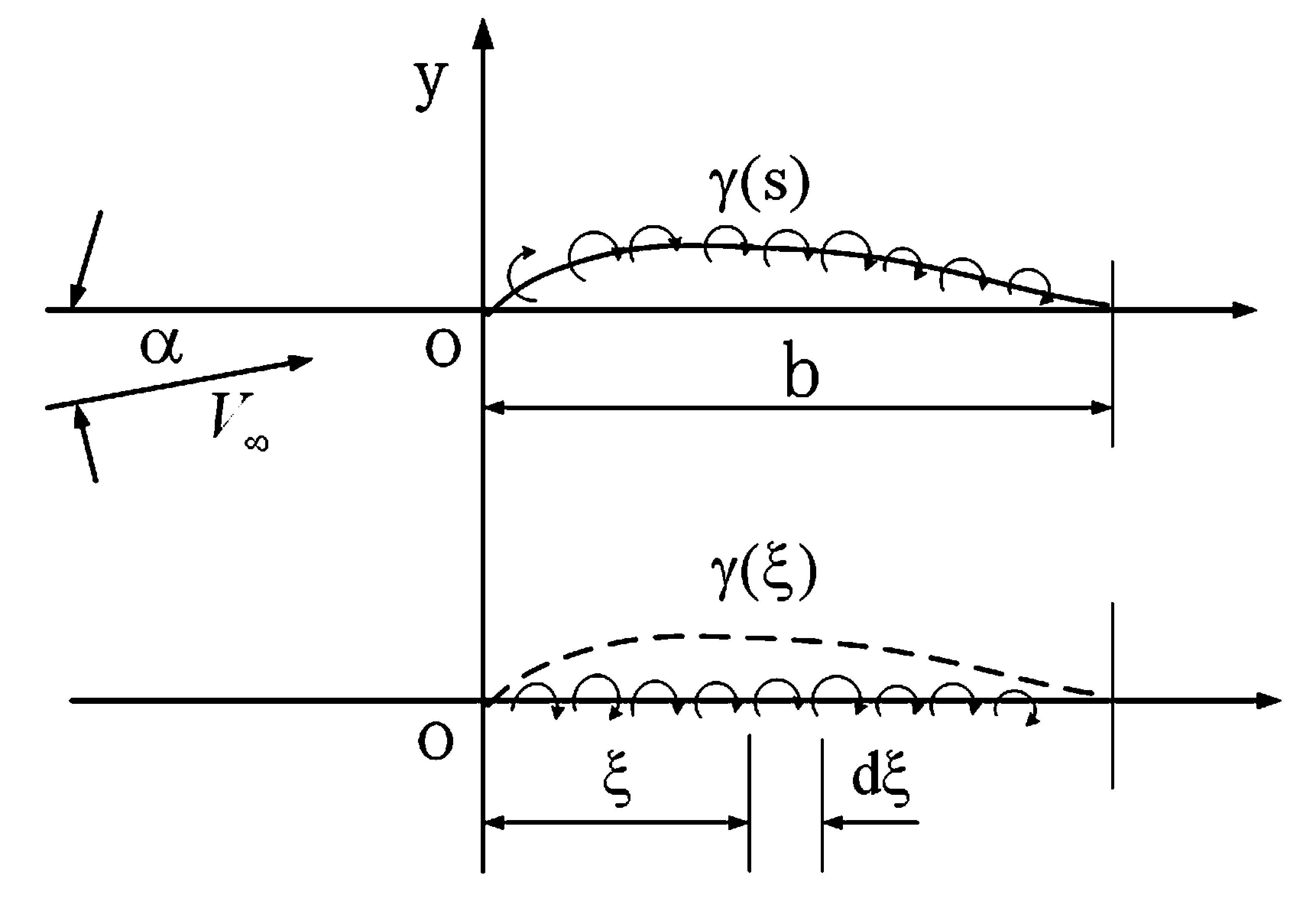
图1 用环量分布代替实际翼型Fig.1 Replacement of the actual airfoil by using the ring distribution

整个翼型的总环量可表示为:

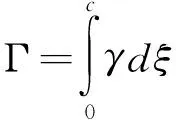
(1)

流场假设条件为无粘、无旋、不可压. 物面边界条件要求流体光滑流过翼型表面:由涡面产生的法向诱导速度Vn和来流引起的法向速度wn的叠加应等于0,即全部涡对翼型上某一点的诱导速度和来流的合速度恰与该处的中弧线相切.边界条件要求流体光滑流过翼型表面,从而得到边界条件为:

(2)

根据毕奥-萨瓦尔定理,边界条件可以转化为如下表达式:

(3)

其中γ(θ)是γ(ξ)的傅氏级数表达形式:

(4)

(5a)

(5b)

根据薄翼型理论,得到总的环量公式为:

(6)

翼型的升力为:

(7)

参考文献[29]中指出当变体机翼折叠角速度较小时,能够忽略非定常气动力效应. 利用准定常假设来简化计算机翼折叠过程中变体飞机的气动力:认为在机翼折叠的任一瞬时,全机的气动力仅取决于该瞬时飞机的静态构型和飞行状态,从而推导出机翼折叠过程中气动力的解析表达式.

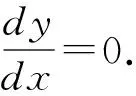
α-A0=0

(8)

其他各项系数An都为0. 将An值代入式(6)得总环量:

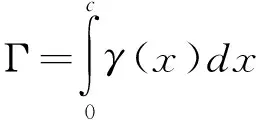
=παcV∞

(9)

单位翼展的机翼升力是:

L=παρcV∞2

(10)

根据折叠机翼实际展开折叠的运动状况,将模型的折叠角度θ设为0°～150°范围内,根据Z型折叠机翼的特点,可得到:

当θ≤90°时,

Δp=(l1+l2cos(π-θ)+l3)·L

=παρcV∞2(l1+l2cosθ+l3)

(11a)

当θ≥90°时,

Δp=(l1+l2cosθ+l3)·L

=παρcV∞2(l1+l2cosθ+l3)

(11b)

因此,作用在Z型折叠翼上的气动力表达式为:

Δp=(l1+l2cosθ+l3)·L

=παρcV∞2(l1+l2cosθ+l3)

(12)

其中θ为折叠角,α为迎角,c为翼型的弦长,ρ为来流的气体密度.

2 Z型折叠机翼的动力学建模

引用文献[30]的模型,将Z型折叠机翼的内翼,中间翼和外翼分别简化为内板、中间板和外板. 内板最左端是固定端,与机身相连接,外板外端是自由端. 折叠角为θ,为内板与中间板以及中间板与外板的夹角.Oixiyi是原点Oi位于三块板最左端点的局部坐标系,全局坐标Oxy与局部坐标O1x1y1重合,Xi与Yi(i=1,2,3)是设置在各板的中心层上,板的轴向为X轴,横向为Z轴,与横向垂直的方向为Y轴,如图2所示.

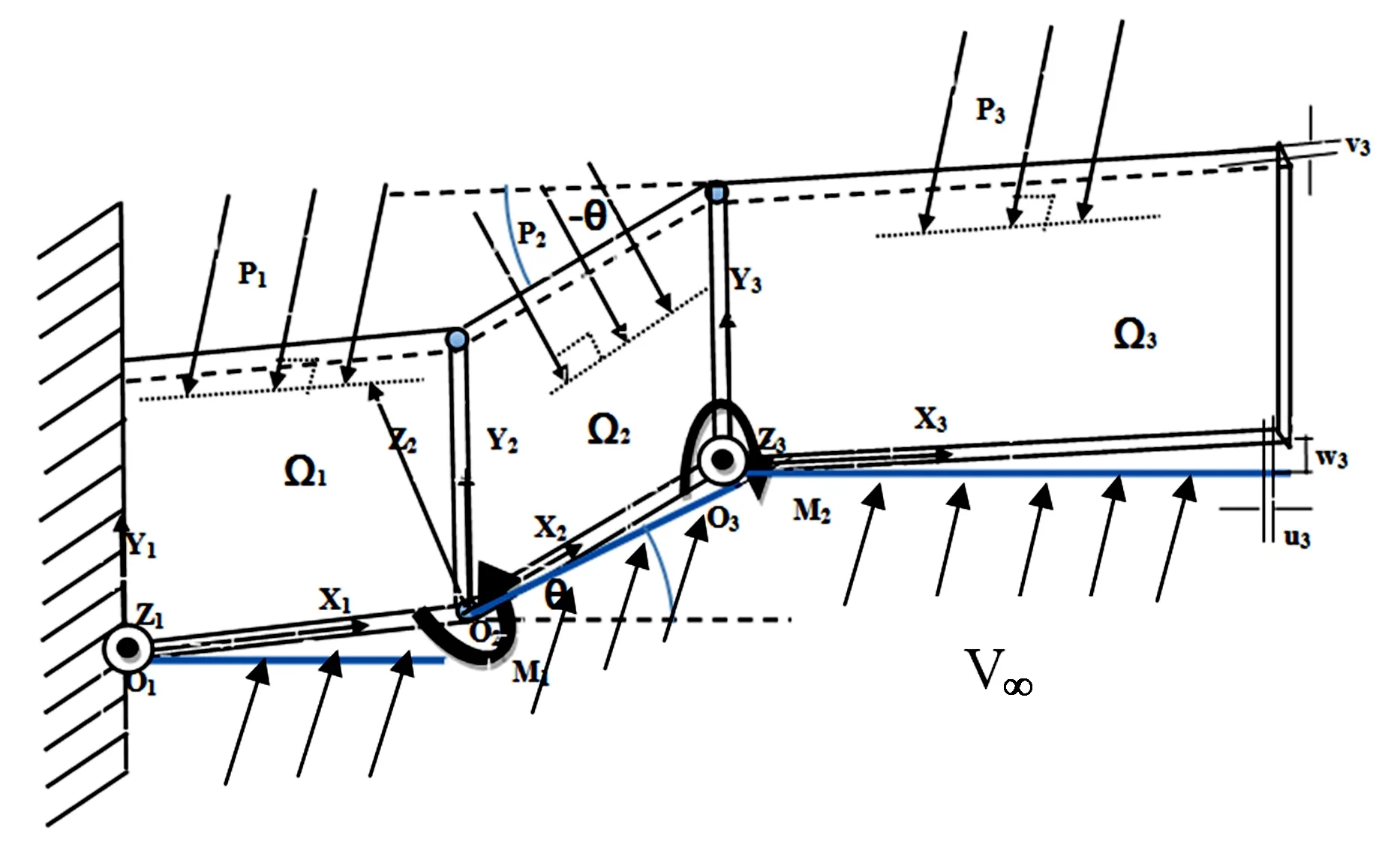
图2 Z型折叠板的理论几何模型Fig.2 Theoretical geometry model of the Z type folding plates

根据Z型折叠机翼在实际飞行过程中的展开和折叠运动的实现方式,做如下假设:

(1) Z型折叠板结构的最左端是理想固支,最右端是自由端；

(2) Z型折叠板折叠角处是理想的刚性铰链连接；

(3) Z型折叠板在变形的过程中,内板和外板始终保持平行；

(4) Z型折叠板的三块板是等厚度、等宽度的.

根据折叠机翼折叠角设为0°～150°范围内,在第一个铰链处施加力矩M1作为驱动力,为Z型折叠机翼提供折叠角速度. 在第二个铰链处施加与M1方向相反的力矩M2,使外板与内板始终保持平行,将上述得到的亚音速下的气动力表达式作用于折叠机翼模型的三块板表面.

由于实际情况中,内板的振动非常小,所以下面主要研究中间板和外板在气动力作用下的非线性振动响应.

根据文献[19]的假设,根据Hamilton原理,得到气动力作用下的Z型折叠板用广义位移表示的非线性动力学方程为:

中间板X、Y、Z方向的动力学方程为:

(13)

(14)

(15)

外板在X、Y、Z方向的非线性动力学方程为:

(16)

(17)

(18)

得到结构整体的边界条件满足:

(19a)

(19b)

(19c)

三块板之间的连接条件为

(20a)

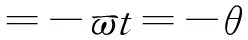
(20b)

3 Galerkin离散

为了方便分析,对上述变量进行无量纲处理,并利用Galerkin方法对结构的非线性运动方程(13)～(18)进行离散,根据文献[30]中ANASYS模拟得到的Z型折叠机翼结构的振动模态,选取横向的前四阶振动模态函数形式为:

ri1=Xi1*Y1,ri2=Xi1*Y2,

ri3=Xi2*Y1,ri4=Xi2*Y2

(21)

其中i为表示第i个板,i=2是中间板,i=3是外板,b是板的宽度.

式(21)中的函数表达式假设为:

Xi1=Ai1cosh(ki1x)-Ai2cos(ki1x)-

Ai3βi1sinh(ki1x)+Ai4sin(ki1x)

Xi2=Bi1cosh(ki2x)-Bi2cos(ki2x)-

Bi3βi2sinh(ki2x)+Bi4sin(ki2x)

(22)

其中:

(23)

由于X和Y两个方向的振幅较小,所以选取模态函数如下:

前两阶X方向振动模态函数为:

(24a)

(24b)

前两阶Y方向振动模态函数为:

(25a)

(25b)

气动力为:

(26)

其中积分区间是在(0,L1)、(L1,L2)、(L2,L3)区域内带入实际参数,得到中间板和外板的两自由度的非线性运动控制方程.

中间板二自由度常微分运动控制方程为:

α216w22θcosθ+α217w21u21+α218w21u22+

(27a)

α226w22θcosθ+α227w21u21+α228w21u22+

(27b)

外板的二自由度常微分运动控制方程为:

(27c)

(27d)

其中方程(27a),(27b)的参数中包含有位移量和加速度量相互耦合,这是由于中间板的转动而产生的项.

4 数值模拟

本文用数值模拟方法研究了亚音速气动力作用下Z型折叠板在折叠过程中的非线性振动响应. 折叠机翼的大幅度变形必然引起飞机的转动惯量、 重心位置、 焦点位置等一系列机体特性的改变,飞机的动力学响应特性也随之改变.因此,需要研究随着折叠角的变化,导致气动力的改变,对结构非线性振动响应产生的影响.通过分叉图,波形图、相图、庞加莱截面等描述了系统的非线性动力学行为.

根据实际参数选取范围无量纲后得到所选取的参数为:

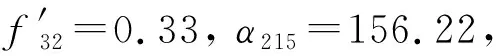
α216=12.65,α217=34.43097,α218=5.53,

α219=16.57,α2110=20.17314,

α2111=14.545,α2112=12.48,α2113=6.3,

α2114=12.4521,α225=43.681,

α226=136.159,α227=16.76282,

α228=20.17314,α229=19.90773,

α2210=24.153579,α2211=23.21,α2212=12.67,

α2213=13.44,α2214=2.345,α311=145.225,

α312=34.36,α313=32.1546,α314=24.56,

α315=10.136,α316=8.1,α321=81.34,

α322=143.772,α323=20.176,α324=21.76,

α325=13.36,α326=8.7.

根据方程(27),研究结构在气动力作用下,折叠机翼结构展开过程中振动响应的变化情况.当折叠角度从30°变化到150°的过程中,得到Z型折叠板的中间板横向位移的分叉图,如图3所示. 从分叉图中分析可得,系统出现了周期和混沌运动的交替变化. 折叠角度在30°逐渐增大的过程中,系统开始从概周期运动进入到周期运动的状态,直到折叠角度达到90°时,系统达到最稳定的状态,折叠角从90°到150°变化的过程中,系统从周期运动进入了混沌运动的状态, 当折叠角度大于135°时,系统出现了混沌运动.

图3 折叠角度θ分叉图Fig.3 Bifurcation diagram of the folding angle θ

下面给出在具体选取折叠角度30°、60°、90°、120°、150°时,Z型折叠板中间板和外板的波形图和三维相图、庞加莱截面.其中,(a) (b)为中间板波形图,(c) (d)为中间板的庞加莱截面图,(e) (f)为外板的波形图,(g)为外板和中间板的三维相图.

当θ=30°时系统的振动情况为:系统中间板和外板均出现概周期运动,且外板的振幅大于中间板的振幅,如图4所示.

当θ=60°时系统的振动情况为:中间板、外板振动情况均与折叠角度为30°时一致,中间板和外板的振动振幅与折叠角度为30°时相比有所减小,如图5所示.

当θ=90°时,系统的中间板和外板振动情况最为稳定,中间板在两个模态上均出现多倍周期运动,振幅达到最小值.外板在两个模态上出现多倍周期运动,振幅没有太大变化.

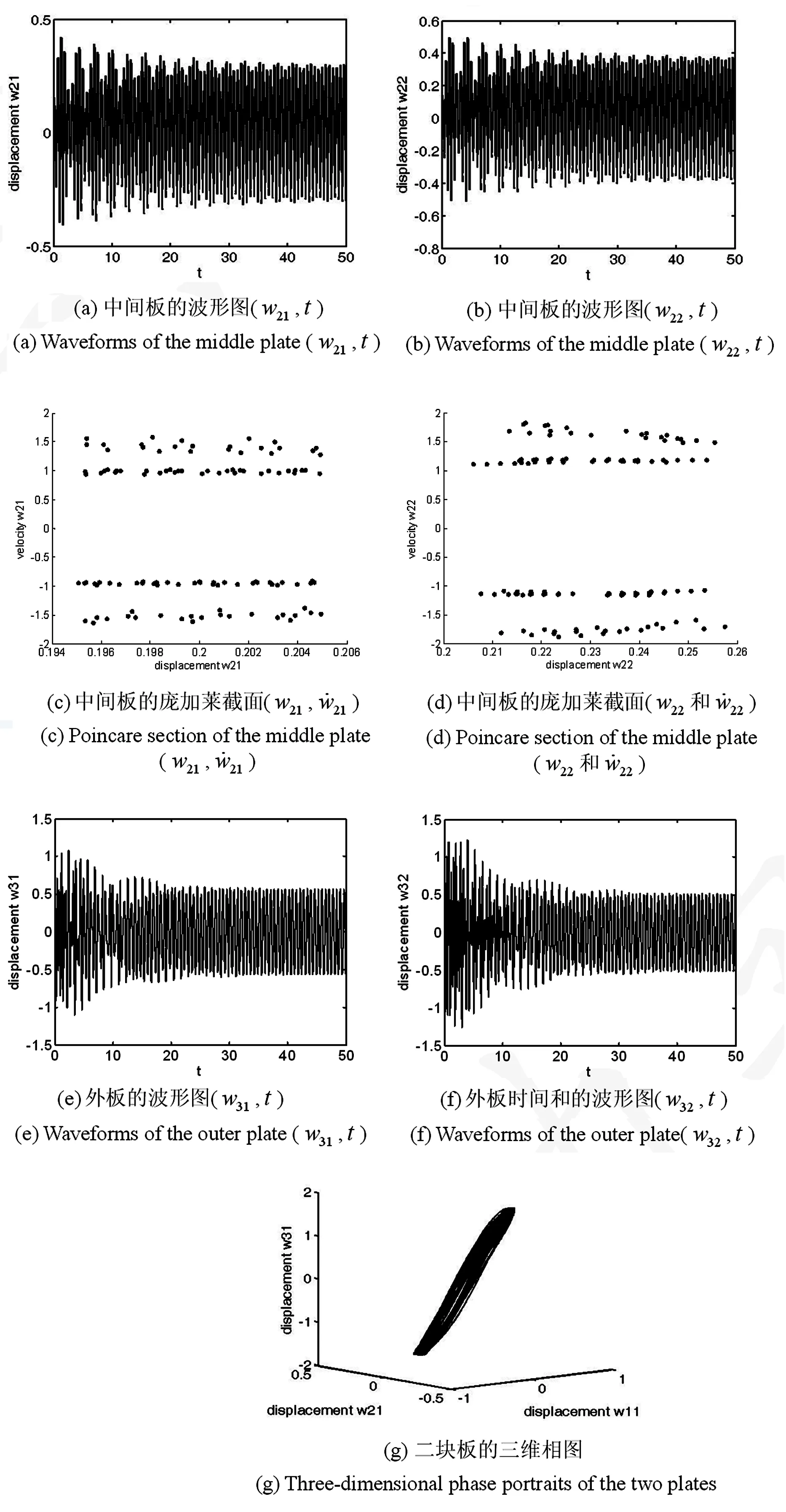
图4 折叠角度为30°的折叠板的运动Fig.4 Period motion of the folding plate with folding angle of 30°

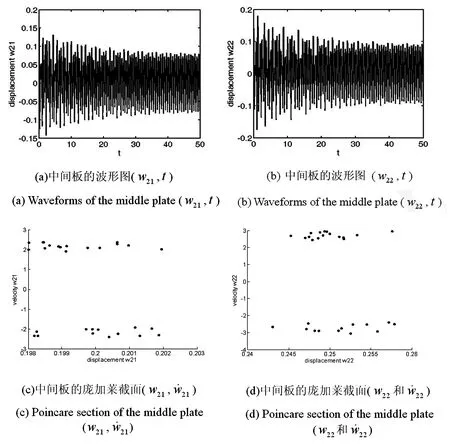
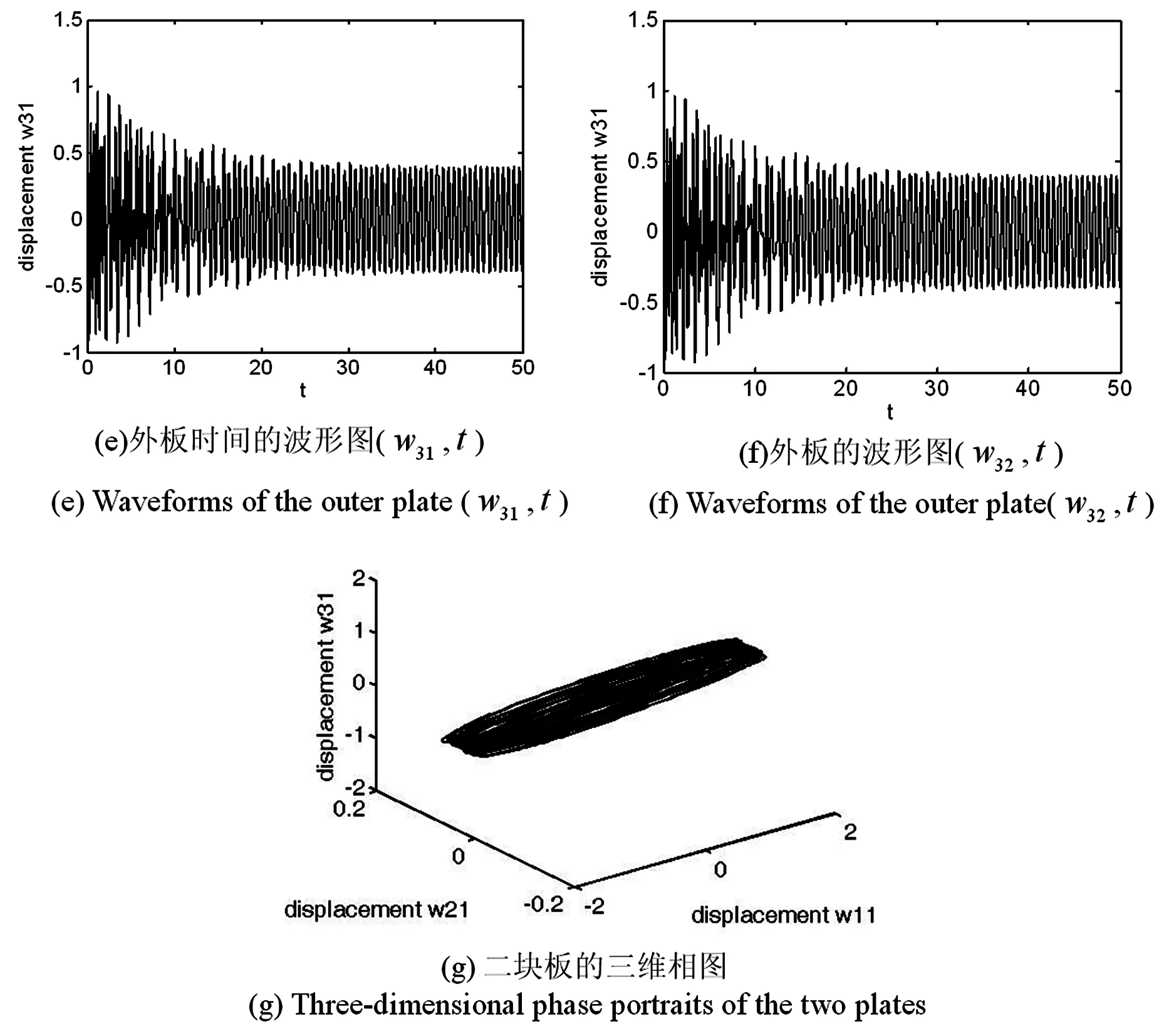
图5 折叠角度为60°的折叠板的运动Fig.5 Period motion of the folding plate with folding angle of 60°

图6 折叠角度为90°时折叠板的运动Fig.6 Period motion of the folding plate with folding angle of 90°

当θ=120°时,系统的中间板振动情况较为稳定,系统中间板在两个模态上均出现多倍周期运动,振幅相对于90°时有所增大. 外板在两个模态上出现概周期运动,振幅相比之前有所增大.

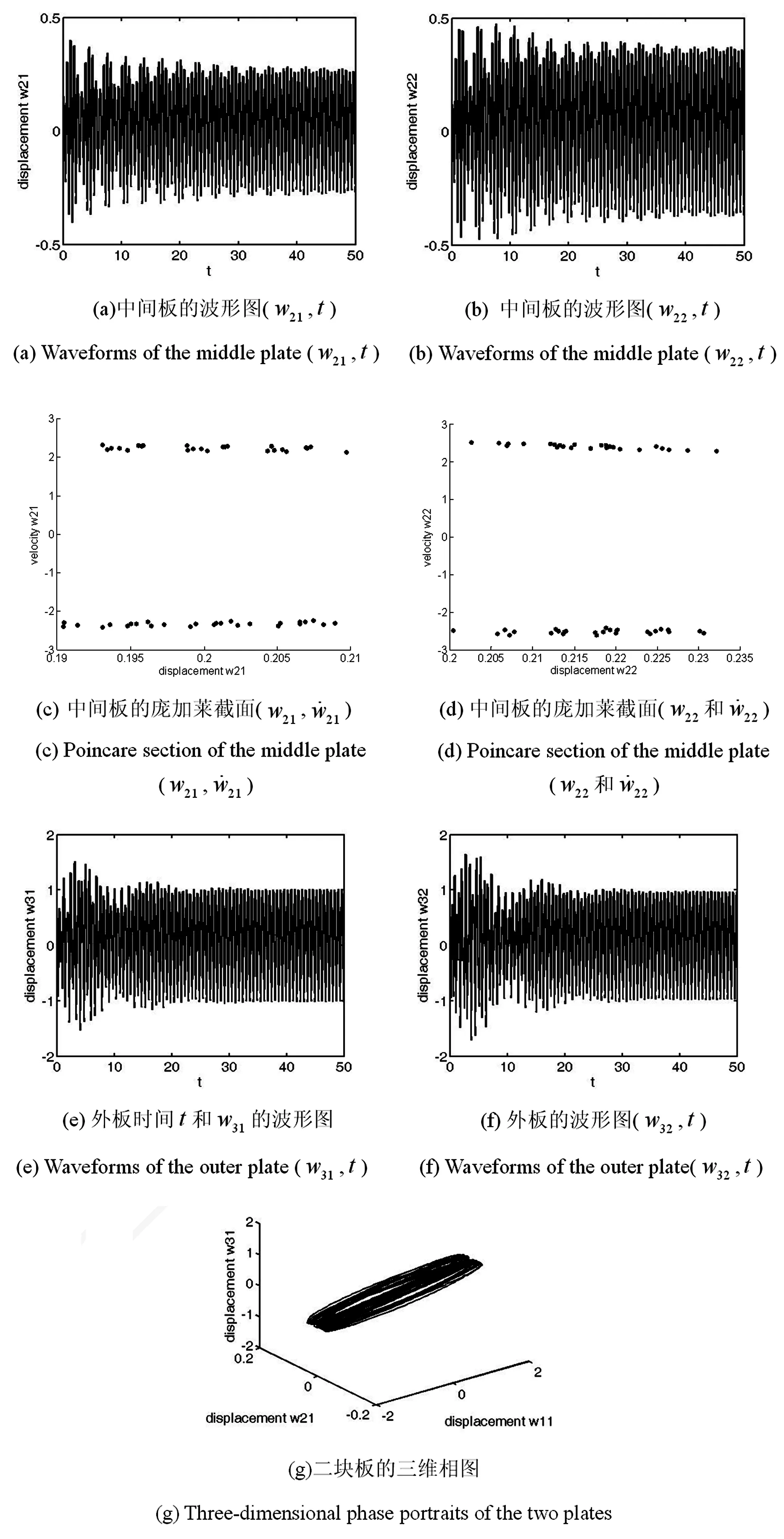
图7 折叠角度为120°时折叠板的运动Fig.7 Period motion of the folding plate with folding angle of 120°

当θ=150°时系统的振动情况为:系统中间板在两个模态上均出现混沌运动. 系统外板在两个模态上均出现概周期运动,如图8所示.

通过数值分析可知,折叠机翼本身的机构变形导致了作用在机翼上气动力的变化,对系统的运动稳定性有一定的影响. 折叠角度从30°到150°变化过程中,在Z型折叠板结构其他参数保持不变的情况下,折叠角度的变化对结构非线性振动响应有一定的影响.

图8 折叠角度为150°时折叠板的运动Fig.8 Period motion of the folding plate with folding angle of 150°

具体分析如下:

(1)折叠角从30°到150°变化过程中,随着折叠角度变化,中间板的振幅变化趋势为先减小再增大,折叠角为90°时,中间板的振幅达到最小值；

(2)外板的振幅在折叠角小于90°时没有太大变化,在折叠角从90°到150°的变化过程中逐渐增大；在90°时达到最稳定的状态；

(3)折叠角小于90°时系统的振动状态相对于折叠角大于90°时更为稳定；

(4)折叠角的变化会影响Z型折叠机翼的气动特性,折叠角在30°到135°这个范围内时,系统的运动状态比较稳定.

5 结论

本文主要研究了Z型折叠机翼的气动力计算及非线性动力学分析,推导了在理想不可压流体来流条件下,利用Kutta-Joukowski升力定理、薄翼型理论,推导出Z型折叠机翼气动升力的解析公式. 应用Hamilton原理建立了在气动力载荷作用下Z型折叠板的非线性动力学方程,利用Galerkin方法对所得到的Z型折叠板模型的偏微分方程进行离散,得到了带有折叠角度的四自由度常微分非线性动力学方程. 利用数值方法分析了Z型折叠板模型在不同折叠角度下的非线性动力学特性,分析了折叠角对机翼稳定性的影响.

根据研究结果发现,折叠角对系统的稳定性有着重要的影响. 当折叠角度在30°到135°这个范围内时,系统可以达到一个相对稳定的状态. 当折叠角度为90°时,系统处于最稳定的状态. 折叠角小于90°时系统的振动状态相对于折叠角大于90°时更为稳定.