深孔轴线直线度误差评定方法*

李 晓， 包建东

(1. 南京理工大学 机械工程学院， 江苏 南京 210094； 2. 南京理工大学 自动化学院， 江苏 南京 210094)

0 引 言

根据形状误差的国家标准及国际标准， 直线度误差定义为被测实际直线相对于理想直线的偏差， 该理想直线应符合最小条件[1]. 直线度的优劣会影响产品的性能及寿命等指标， 因此直线度误差的评判是一个重要的课题. 目前， 深孔轴线直线度误差评定的方法主要有： 端点连线法、 最小二乘法、 最小区域法. 其中前两种方法属于近似评定， 一般不能满足最小条件. 为此， 国内外学者研究了许多基于最小包容区域原则的方法： 计算点数较少时采用计算几何评定方法如凸多边形法、 极值搜索法等， 优化方法如遗传算法、 粒子群算法等， 以尽可能真实地反映直线的直线度误差. 不同的评定方法对直线度误差结果影响较大， 进而影响对产品质量的判断， 故而有必要进行深孔直线度误差评定方法的研究[2].

1 评定方法

本文通过介绍几种常见直线度误差评定方法的原理， 并以深孔光电检测实验采集的坐标数据为例， 分别用5种方法对其进行直线度评定， 并比较各方法优劣和评定精度. 采用某实验中采集的3组深孔坐标数据， 每组10个测量点， 将原始坐标转换为偏心距， 转化后的轴向位置x及偏心距y数据如表 1 所示.

表 1 偏心距数据

1.1 端点连线法

建立如图 1 直角坐标系xoy，x轴表示轴向位移，y轴表示光电坐标偏心距.

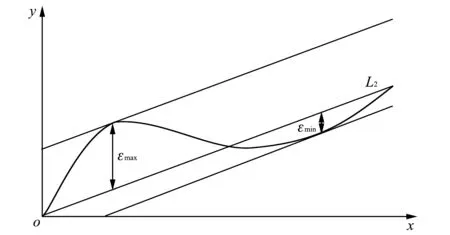
图 1 端点连线法原理示意图Fig.1 Endpoint connection principle diagram

连接首末两点， 直线L1方程为

(1)

式中：x0，y0为起点坐标值；xe,ye为终点坐标值.

计算误差曲线上各点(xi,yi)到直线L1的偏差(有正负)

εi=yi-fi

(2)

作包容所有点的L1的平行线， 那么两平行线在y轴上的距离

p=εmax-εmin

(3)

即为直线度误差值[3].

1.2 最小二乘法

根据表 1 数据计算最小二乘直线方程

f=ax+b,

(4)

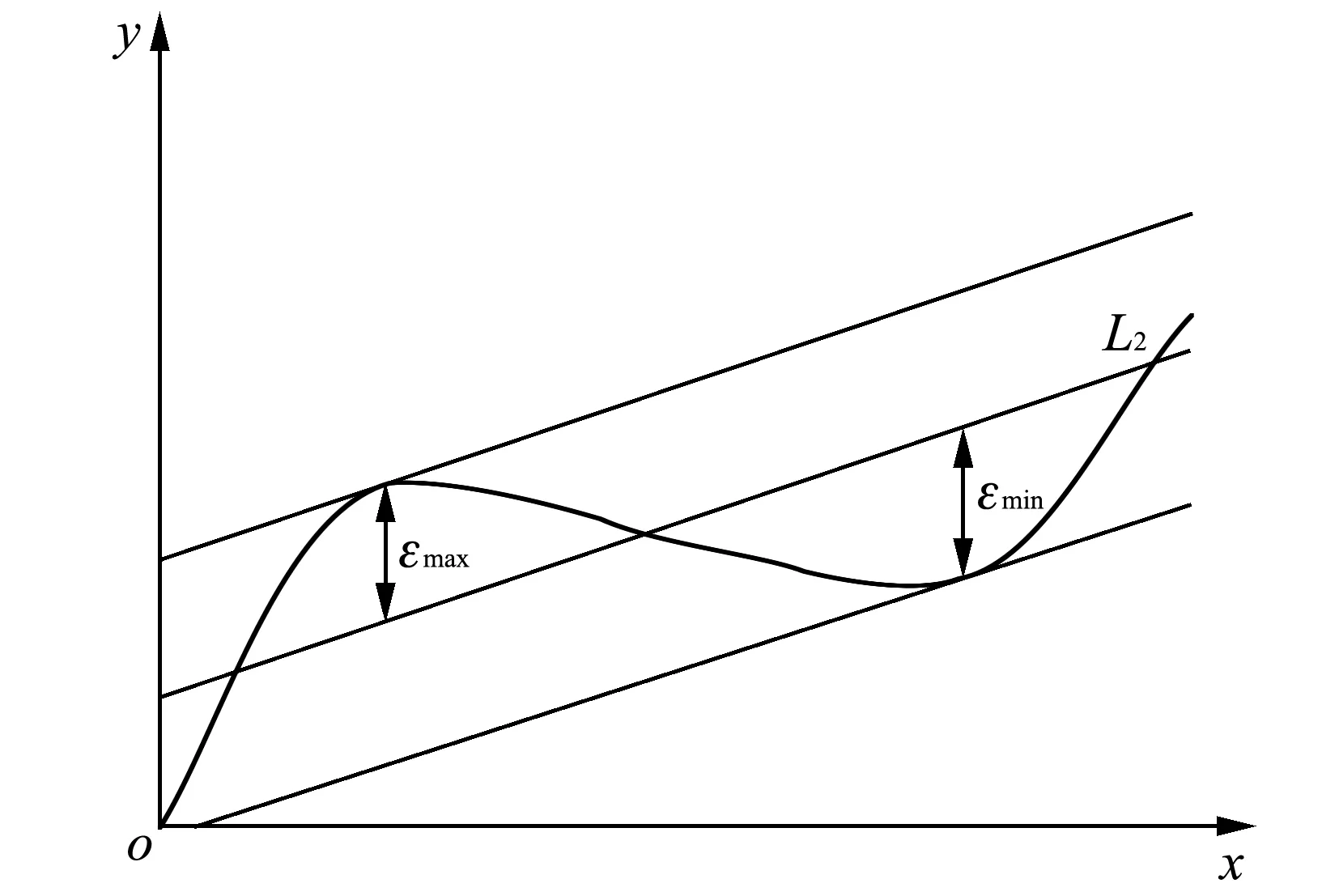
图 2 最小二乘法原理示意图Fig.2 Least square method principle diagram

式中：n为测量点数；

(5)

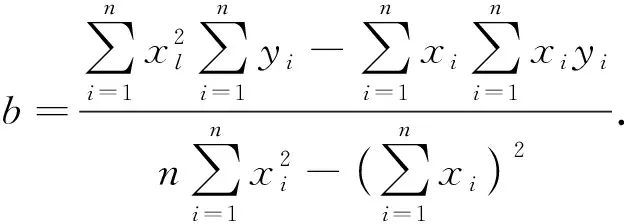
(6)

计算误差曲线上各点(xi,yi)到如图 2 直线L2的偏差(有正负)

εi=yi-fi.

(7)

求出εi中的最大值和最小值， 作包容所有点的L2的平行线， 那么两平行线在y轴上的距离

p=εmax-εmin

(8)

即为直线度误差值[4].

1.3 极值搜索法

计算最小包容区域主要是寻找到满足条件的“低-高-低”或“高-低-高”3点.

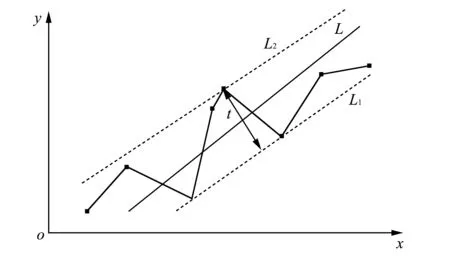
图 3 极值搜索法原理示意图Fig.3 Extreme search principle diagram

如图 3， 以最小二乘拟合直线L为基线， 称基线上侧为高点区， 下侧为低点区， 分别在两侧寻找满足条件的平行包容线组， 计算其间距. 找出所有满足条件的包容线间距ti(i=1,2,3……n)中的最小值tmin， 作为所求直线度误差[5].

如图 5(c) 对于第一组测量数据最小包容区域计算中， 低点连线为下包容线且满足间距为最小值时， 下包容线方程为

0.11x-60y+37.97=0,

(9)

这对包容线L1h、L1l间的距离为t1=0.440 mm. 高点连线为上包容线且满足间距为最小值时， 上包容线方程为

0.001x-45y+52.28=0.

(10)

这对包容线L2h、L2l间的距离为t2=0.521 mm. 则最小区域法直线度误差即为tmin=0.440 mm.

1.4 分割逼近法

基于分割逼近法提取理想直线的思路是： 拟合最小二乘直线如式(4)， 并以此为起始直线进行搜索， 在一定的角度范围内以最小二乘直线斜率的变化量δa为间隔进行分割， 寻找满足最小区域的理想基准直线. 如图 4 所示实线为最小二乘线， 虚线为

f′=(a±m·δa)x+b,

(11)

图 4 分割逼近法原理示意图Fig.4 Segmentation approach principle diagram

也即初始直线绕Q点逆时针和顺时针分别旋转角度， 计算对应于所设角度范围内所有分割线的直线度误差值pi， 其中最小值min(pi)就是符合最小包容区域的直线度误差值， 对应于min(pi)的直线就是符合最小包容区域的理想直线[6].

本例中逆时针和顺时针所设角度范围θ分别为1.5°， 分割次数m分别为240， 那么对应的角度增量或减量为0.37′,斜率变化量δa=1×10-4. 根据上述分割逼近原理， 得到如图5(d)所示结果， 由于分割线较密集， 图中仅展示5条分割线， 其中点划线即为所得理想直线， 斜率为0.001 822， 实线表示初始直线.

1.5 遗传算法

遗传算法以生物进化为理论基础， 总体来说是一个不断迭代更新的过程. 首先提取出问题的解对其进行编码构成“染色体”， 作为种群中的个体. 根据目标函数得到适应度函数， 由此算出个体的适应度值， 通过选择、 交叉、 变异一系列操作使种群完成新一代的进化， 这样一代一代不断更新最终求得最优解[7-8]. 算法步骤为：

1) 编码构成初始种群A0(t).

2) 计算个体适应度

h(k)=gmax-g(k),

(12)

式中：g(k)为目标函数

3) 选择操作， 根据适应度大小得到n个新个体A1(t).

4) 交叉操作， 形成A2(t).

5) 变异操作， 形成新一代A3(t+1).

6) 检查进化代数.

7) 保存适应度最大的个体， 求出对应的目标函数值即为直线度误差.

评定过程中所需参数设置为： 种群规模n=50； 交叉概率pc=0.6； 变异概率pm=0.02； 最大进化代数t=1 000. 算法运行优化迭代过程如图5(e)所示.

根据表 1 偏心距数据， 采用计算机辅助工具对数据进行仿真， 第一次测量数据的曲线图分别如图5(a)～图 5(e) 所示.

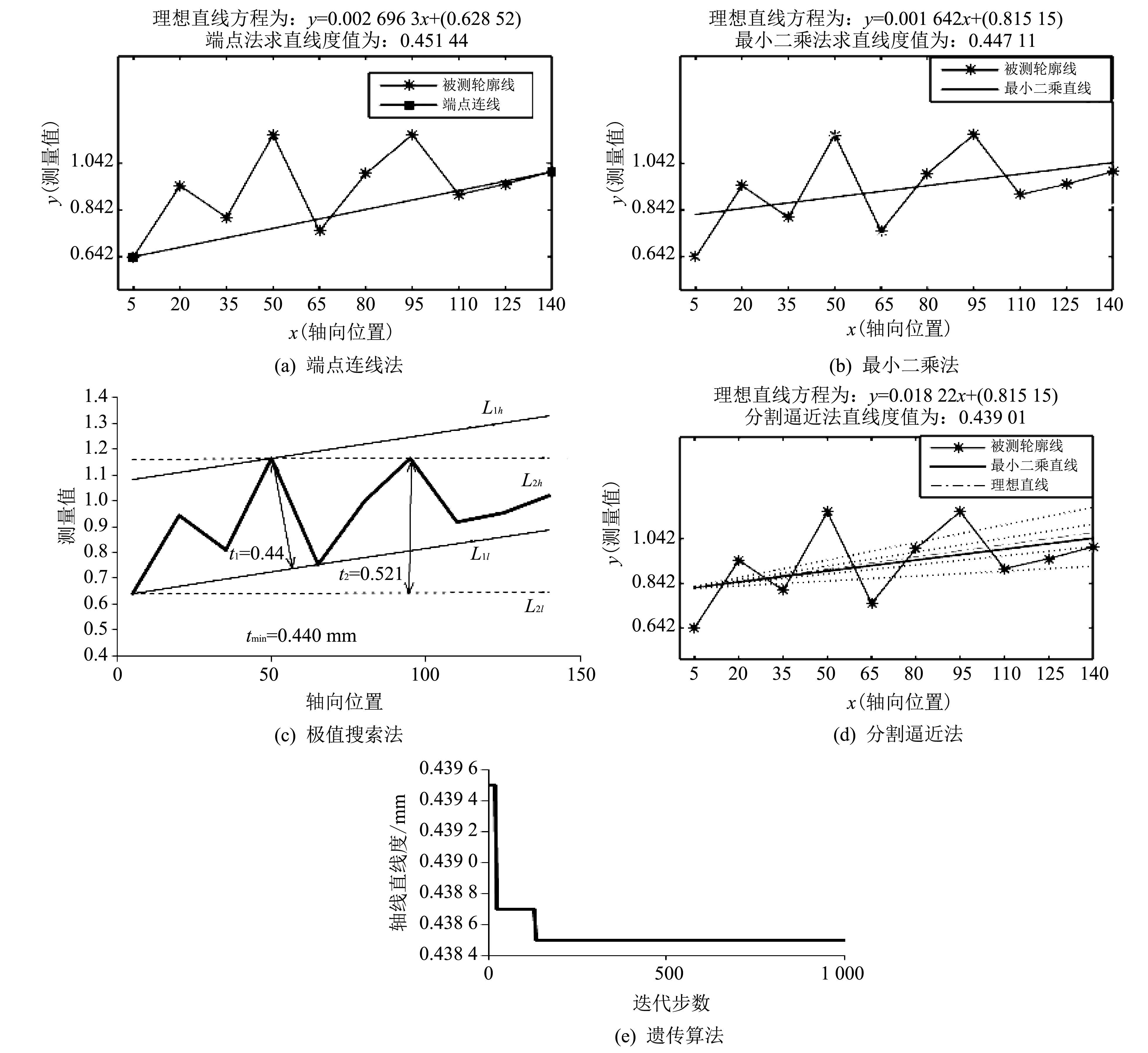
图 5 评定直线度曲线Fig.5 Assess the straightness curve

2 结果比较

对各方法3组结果求平均值， 最终结果如表 2 所示.

仿真结果表明， 端点连线法和最小二乘法评定结果最大； 极值搜索、 分割逼近和遗传算法此3种方法评定出来的误差较前两种方法精度均有提高， 遗传算法评定的直线度误差比端点连线法提高约4.4%， 比最小二乘法提高约3.4%， 其精确度高， 理论上可以无限逼近真实值. 由此可以看出： 通过最小包容区域原则评定直线度的误差是最小的. 此外， 本文采用的数据点数一定程度上限制了评定精度， 实际应用中可通过适当增加采样点， 或每轮采样交错选取采样点来进一步提高直线度误差评定精度.

表 2 各算法计算结果

表 3 结果比较

4 结 论

通过研究深孔轴线直线度误差评定方法和进行计算机仿真实验可知： 几种方法均可对深孔直线度误差进行评估， 其中， 最小区域法直线度误差值小精度高， 计算过程较复杂， 但借助计算机程序容易实现， 而端点连线法和最小二乘法精度较低但计算简单. 实际应用中可根据产品对象和精度要求选择合适的评定方法， 或采用多种方法的计算结果进行综合评估.