基于流形分离技术的DOA和极化参数联合估计方法*
2018-10-11胡显智戴旭初
胡显智, 王 宁, 戴旭初
(1. 中国科学技术大学 信息科学技术学院, 安徽 合肥 230027;2. 南京电子技术研究所, 江苏 南京 210039)
0 引 言
信号多维参数估计是阵列信号处理的重要任务之一. 相较于由增益特性完全相同的多个天线组成的标量阵列, 极化敏感阵列(polarization sensitive array)利用内部阵元极化选择特性的多元化获取信号的极化信息, 被证明可有效提高参数估计的性能[1,2]. 针对DOA和极化参数的联合估计问题, 诸多有效算法被陆续提出: 文献[3]提出了pencil-MUSIC算法, 可得到高精度的二维DOA和极化参数的联合估计, 但计算量较大; 文献[4,5]将ESPRIT算法推广到极化敏感阵列, 得到了低复杂度的参数估计算法, 但其只适用于特定结构的阵列. 此外, 针对相干信号源的DOA和极化参数联合估计, 虽然也出现了一些算法, 如空域平滑方法[6]、 极化域平滑方法[7]等, 但这些方法只对部分具有特殊结构的阵列有效; 实现一般结构的极化敏感阵列下相干信号源的参数估计仍然是一个难题.
流形分离技术(MST)是一种对阵列接收数据建模的新方法, 该技术源于波形域建模(wavefield modeling[8,9])思想, 即将阵列的接收数据中与信号相关的部分表示为阵列对入射信号波场的采样. 基于这一思想, Belloni等人提出了流形分离的概念, 并利用MST将信号导向矢量分解为采样矩阵和一个范德蒙德结构矢量的乘积, 进而将root-MUSIC算法推广到任意结构阵列[10]. 随后, Costa等人进一步考虑了方位角和俯仰角联合估计的情况, 利用MST得到了适用于任意结构阵列的低复杂度二维DOA估计方法[11].
本文进一步将流形分离技术拓展到极化敏感阵列中, 研究任意结构的极化敏感阵列下DOA和极化参数的联合估计方法. 同时兼顾信号源部分相关和完全相干的情况. 特别是本文算法在未知阵列结构的确切参数, 但是能够获得实测的阵列标定数据(array calibration measurements[10])时仍然有效, 具有重要的实际应用价值.
1 信号和阵列模型

X=Aθ,φ,γ,ηS+N,
(1)
式中:S∈CK×L和N∈CM×L分别为信号采样矩阵和噪声采样矩阵. 阵列流形矩阵A=[aθ1,φ1,γ1,η1,…,aθK,φK,γK,ηk]∈CM×K的第k列为第k个来波对应的信号导向矢量, 其形式为[12]
aθk,φk,γk,ηk=Uθk,φkβΞθk,φkhγk,ηk,
(2)
式中: 对角阵U为信号的空域相位矩阵;β被称为极化敏感阵列的极化敏感矩阵, 每行代表相应阵元对信号波场的响应特性;Ξ(θk,φk)=[εh,εv]由水平方向矢量εh=[-sinθk,cosθk,0]T和垂直方向矢量εp=-[sinφkcosθk,sinφksinθk,cosφk]T构成;h=[cosγk,sinγkejηk]T为电磁波的极化矢量, 包含来波的极化信息.
综合上述概念, 可进一步将信号导向矢量写为(为方便表述, 略去了下标k)
aθ,φ,γ,η=[ah(θ,φ),av(θ,φ)]h(γ,η),
(3)
式中:ah(θ,φ)=Uθ,φβεh和av(θ,φ)=Uθ,φβεv被称为水平分量导向矢量和垂直分量导向矢量, 分别表示极化敏感阵列对来自(θ,φ)方向上的水平极化电磁波和垂直极化电磁波的响应.
由于信号源个数的估计方法较多, 也较为成熟, 本文不对信号源个数的估计问题进行讨论. 不失一般性, 假设信号源的个数K和信号子空间维度Ks(即信号协方差矩阵RS的秩)已知.
2 流形分离技术
在阵列信号处理中, 若信号导向矢量具有范德蒙德结构, 会带来诸多的便利, 如root-MUSIC, ESPRIT等高效的快速算法在参数估计问题中的应用; 但这一般要求阵列具有特定的结构(如ULA等). 流形分离技术可将任意结构阵列的信号导向矢量分解为采样矩阵和一个范德蒙德结构矢量的乘积, 其中: 采样矩阵仅与阵列结构有关, 与信号参数无关; 范德蒙德结构矢量仅包含信号DOA参数, 与阵列无关. 这使得在任意结构的阵列下实现参数估计的快速算法成为可能.
具体到极化敏感阵列, 式(3)中的水平/垂直分量导向矢量ah(θ,φ)和av(θ,φ)同时包含信号DOA参数和阵列结构参数; 流形分离技术实质上是寻找一组正交基对信号导向矢量进行正交展开, 从而将导向矢量中与阵列相关的部分和与信号相关的部分相互分离, 即
ah(θ,φ)=Ghd(θ,φ),av(θ,φ)=Gvd(θ,φ),
(4)
式中: 矩阵Gh∈CM×MaMe和Gv∈CM×MaMe即为前面所说的采样矩阵, 这里分别称之为水平分量采样矩阵和垂直分量采样矩阵, 其完全由阵列结构决定; 正交基采用二维傅里叶基矢量d(θ,φ)∈CMaMe×1, 即有
d(θ,φ)=d(θ)⊗d(φ),

(5)
式中: ⊗为克罗内积. 正整数Ma和Me是所截取的模式数: 事实上式(4)中信号导向矢量的正交展开具有无穷多谐波分量(即式(5)中ma→∞,me→∞), 但可证明当ma和me足够大时, 后续谐波分量基本可以忽略不计[13], 从而可截取有限的模式数对信号导向矢量进行建模且保持足够的精度, 便于工程应用(实际应用时, 可根据阵列的有效孔径选取合适的Ma和Me).
结合式(3)和式(4), 得到基于MST的任意结构极化敏感阵列的信号导向矢量模型为
aθ,φ,γ,η=[Ghd(θ,φ),Gvd(θ,φ)]h(γ,η)=G(I2⊗d(θ,φ))h(γ,η),
(6)
式中: 采样矩阵G=[Gh,Gv]∈CM×2MaMe;I2为2×2的单位阵;h(γ,η)为前文提到的信号极化矢量.
现在的问题是采样矩阵Gh和Gv如何求解. 文献[10]利用一种被称为有效孔径分布函数(Effective Aperture Distribution Function)的方法来确定采样矩阵. 具体而言, 分别在θ∈[-π,π]和φ∈[-π,π]内均匀选取Qa(Qa>Ma)和Qe(Qe>Me)个标定点, 得到对应的阵列标定数据
CM×QaMe,

(7)

3 DOA和极化参数联合估计
利用2小节讨论的MST, 可将式(1)中极化敏感阵列的接收数据采样矩阵X重新表示为
X=G(I2⊗D(θ,φ))V(γ,η)S+N,
(8)
式中: 矩阵D(θ,φ)=[d(θ1,φ1),…,d(θK,φK)]∈CMaMe×K包含来波信号的DOA参数; 矩阵V(γ,η)=[Vh(γ),Vv(γ,η]T包含信号的极化参数, 有
Vh(γ)=diag{cos(γ1),…,cos(γK)}∈RK×K,
Vv(γ,η)=diag{sin(γ1)ejη1,…,sin(γK)ejηK}∈CK×K.
(9)
基于式(8)所示的阵列接收数据模型, 下面讨论两种适用于任意结构极化敏感阵列的DOA和极化参数联合估计方法.
3.1 基于MST的极化FFT-MUSIC算法
在零均值圆空-时-极化白噪声的假设下, 阵列接收数据协方差矩阵可表示为
(10)
式中:Es为信号子空间, 由RX的Ks个主特征矢量组成;En为噪声子空间, 由剩余M-Ks个次特征矢量组成, 与Es相互正交. 当满足Ks=K时(即信号源非相干), 可通过搜索式(11)的极小值点获得来波信号参数
f(θ,φ,γ,η)=hH(γ,η)M(θ,φ)h(γ,η),
(11)
式中: 矩阵M(θ,φ)∈C2×2的形式为
(12)
直接对式(11)进行搜索, 需要对信号的角度和极化参数进行4-D联合搜索, 计算量很大. 为减小计算量, 利用相关矩阵理论, 可将其分两步进行:
(13)
式中:Gmin{·}表示矩阵的最小特征值;Gmin{·}表示矩阵最小特征值对应的特征矢量. 由此, 整个4-D搜索过程被分解成一个2-D角度参数搜索过程和一个求解矩阵最小特征值及特征矢量的问题.
以上即为传统的极化MUSIC算法[12]的基本思路, 其中第二步的矩阵M(θ,φ)的最小特征值求解具有简单的闭式表达, 计算量主要集中在第一步中对角度参数的二维搜索中, 其搜索间隔必须取得足够小以满足精度要求, 而相应需要搜索的点就会很多, 由此带来计算量的负担.
利用式(8)所示的阵列输出数据模型, 可得到基于MST的参数估计快速方法: 极化FFT- MUSIC算法. 具体而言, 结合式(6)和式(12), 可将矩阵M(θ,φ)重新表示为


(14)
进一步有
(15)
式中:d(θ)C(2Ma-1)和d(φ)∈C(2Me-1)为一维傅里叶基矢量(见式(5)); 系数矩阵Chh,Chv,Cvh和Cvv的形式为
(16)
式中:a↔h,b↔v; 而∑diag{Π,k}表示矩阵Π第k条(块)对角线上(块)对角元之和, 矩阵左下角元计为k=1.
观察式(15), 2×2矩阵M(θ,φ)的每一项实质都是一个标准的2-D DFT形式, 从而可利用2-D FFT算法快速计算得到
(17)

3.2 基于MST的极化MVP-SSF算法
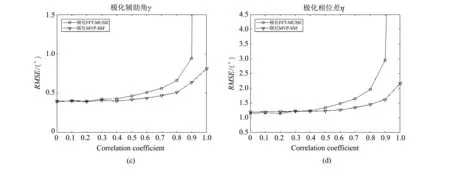
对于信号源完全相干的情况, 即Ks 考虑式(8)~式(10)的阵列模型, 但允许Ks≤K, 此时可利用信号子空间拟合技术得到来波信号的参数估计[14] (18) 目标问题是一个非线性最小二乘问题, 文献[14]采用一种被称为MVP(Modified Variable Projection)的算法对其进行求解. MVP算法实质是对高斯-牛顿法的一种改进, 其通过迭代完成求解 ξi=ξi-1-μH-1V′, (19) 式中:ξi是第i次迭代的结果; 梯度向量V=f(ξ)∈C4K×1, 矩阵H∈C4K×4K是Hessian矩阵2f(ξ)的近似;μ为搜索步长, 保证算法的收敛性. 关于V′和H的具体表达式, 文献[14]中做了详尽的推导, 将其略作扩展即可得到极化敏感阵列下的形式. 然而, 上述求解需要知道阵列流形的显式表达, 在实际中有时可能无法获得阵列结构的确切参数而只能得到实测的阵列标定数据, 此时无法直接使用MVP算法. 此外, 即便可获得阵列的所有参数, 当阵列结构较为复杂时, 计算阵列流形的导数也较为繁琐. 利用式(8)所示基于MST的极化敏感阵列模型, 可以得到V′和H的简单闭式表达, 且其在仅知道实测的阵列标定数据时仍然有效, 这就是极化MVP-SSF算法的基本思想. 具体而言, 利用式(8)的数据模型, 结合文献[14]的讨论, 得到V′和H闭式表达为 (20) 式中: 矩阵Z=[IK,IK,IK,IK]∈RK×4K, ·表示Hardmard积;JA(ξ)∈CM×4K为阵列流形矩阵A(ξ)对ξ的求导, 利用MST有闭式表达 (21) (22) 设模式数Ma=Me=M. 极化MVP-SSF算法单次迭代的计算复杂度约为O(M2MK), 主要体现在JA(ξ)的计算上(GΨ可提前计算好, 不需要参与迭代). 作为一个迭代算法, 极化MVP-SSF算法需要对信号参数进行初步估计作为迭代的初始值. 信号非相干(即Ks=K)时, 极化FFT-MUSIC算法是一个理想的选择, 其估计快速且结果可靠. 对于信号完全相干(即Ks 图 1 8阵元极化敏感阵均匀圆阵Fig.1 Eight-element polarimetric uniform circular array 实验1 考虑如图 1 所示的极化敏感阵列, 它由8个指向不尽相同且均匀分布在圆上的短偶极子天线组成(各阵元皆指向圆心, 其输出电信号正比于与之平行的电场分量), 半径为λ. 两个等功率的非相关信号分别自(θ1=20°,φ1=40°)和(θ2=30°,φ2=50°)的方向入射至阵列; 极化参数分别为(γ1=60°,η1=30°)和(γ2=20°,η2=70°). 快拍数L=200, 噪声为加性高斯白噪声. 独立实验500次, 分别采用传统的极化MUSIC算法和本文的极化FFT-MUSIC算法(Ma=Me=21)进行信号参数估计. 在信噪比SNR=10 dB下, 两算法其中一次典型实现的运行时间及参数估计结果的比较如表 1 所示(搜索间隔为0.25°). 表 1 极化FFT-MUSIC算法与传统MUSIC方法运行时间的比较 图 2 则反映了在不同信噪比下, 两个算法的参数估计根均方误差的变化情况. 图 2 参数估计随信噪比变化的根均方误差Fig.2 RMSE as a function of the SNR 由图 2 可知, 在整个信噪比变化范围内(0~30 dB), 极化FFT-MUSIC算法的统计性能与传统的极化MUSIC算法相比, 几无差别. 这说明即便信噪比达到30 dB, 由于截取有限个(Ma=Me=21)模式所造成的误差与噪声相比仍然足够小, 可以忽略不计. 而根据表1可知, 在同一台机器下, 极化FFT-MUSIC算法进行参数估计所需要的时间远远小于传统MUSIC算法. 综上所述, 极化FFT-MUSIC算法在不损失原极化MUSIC算法估计精度的同时, 有效降低了计算复杂度, 具有更强的实时性. 图 3 参数估计随信号源相关系数变化的根均方误差Fig.3 RMSE as a function of correlation coefficient between the two sources 实验2 考虑半径为2λ的极化敏感均匀圆阵, 阵元数为20个, 每个阵元仍指向圆心. 信号的DOA和极化参数同实验1. 快拍数L=200, 信噪比SNR=10 dB. 独立实验1 000次, 图 3 反映了在不同的信号源相关系数下, 极化FFT-MUSIC算法和极化MVP-SSF算法的参数估计根均方误差的变化情况. 实验中, 两个算法所截取的模式数皆取Ma=Me=41. 由图 3 可知, 在信号源相关度较低时, 极化FFT-MUSIC算法和极化MVP-SSF算法的精度基本相当; 而当相关系数大于0.6后, 极化MVP-SSF算法的参数估计性能要明显优于极化FFT-MUSIC算法. 特别是当信号源完全相干时(相干系数为1), 极化FFT-MUSIC算法已然失效, 而极化MVP-SSF算法仍然具有良好的性能. 由此可见, 极化MVP-SSF算法可以很好地解决强相关源乃至相干信号源的参数估计问题. 本文将流形分离技术(MST)拓展到极化敏感阵列信号处理中, 研究了两种DOA和极化参数的联合估计方法: 极化FFT-MUSIC算法和极化MVP-SSF算法, 它们皆适用于任意结构的极化敏感阵列. 实验结果表明: 极化FFT-MUSIC算法具有与传统极化MUSIC算法基本相同的性能, 而计算复杂度有效降低; 极化MVP-SSF算法则可以实现一般结构的极化敏感阵列下强相关源乃至相干信号源的参数估计.
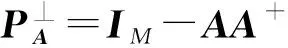


4 实验及结果分析





5 结 论
