大断面悬臂浇筑箱梁0号块非线性分析

聂立力 王吉文 张全阳

(中国市政工程中南设计研究总院有限公司 武汉 430000)

桥梁设计中，一般先采用杆系模型进行全桥整体分析，然后对特殊部位采用精细化模型做进一步的局部分析，以此掌握关键部位的应力情况，用于指导设计、施工工作。悬臂浇筑箱梁的0号块梁段处于墩顶横梁及附近处，梁顶缘处于纵向、横向、竖向三向预应力筋的高应力区，大吨位支座使梁底处于弯剪压状态，横梁中设置的人孔容易产生局部应力集中，因此，该处应力状态复杂，是设计的关键部位，对0号块的应力分布状况和应力大小进行计算分析是十分必要的。本文依托于浠水县浠水四桥工程，利用有限元软件Abaqus，对该桥的0号块进行非线性有限元分析，以期得到对混凝土箱梁的设计与施工具有意义的分析结果。

浠水四桥主桥上部结构采用预应力混凝土变截面连续箱梁，桥跨布置为72 m+112 m+72 m=256 m。下部结构主桥主墩采用圆端形空心墩，桥墩采用钻孔桩基础。主桥上构采用预应力混凝土变截面连续箱梁，为三向预应力结构。箱梁为单箱三室直腹板截面，顶宽26.0 m、底宽19.0 m、两侧翼缘宽3.5 m。连续箱梁中支点断面见图1，梁高6.8 m，跨中梁高为2.8 m。箱室底板采用变厚度布置，支点处厚为85 cm，跨中厚为30 cm，底板下缘曲线为2次抛物线。箱室顶板厚度为28 cm，翼缘板端部厚度18 cm。箱室断面共有4个腹板，腹板厚度由支点处经一次渐变(3个施工节段)至跨中，厚度由80 cm渐变至50 cm，见图2。

图1 零号块中支点横断面图(单位：cm)

该桥主要特点为：采用整幅挂篮对称悬臂浇筑施工，桥宽达26 m，混凝土采用C55标号，单侧共采用4套菱形挂篮，节段最大混凝土体积达到106 m3，单侧挂篮及模板总质量达到120 t；成桥后支座反力达66 500 kN，采用特制的QZ-70 000 kN支座。而0号块施工时采用一次浇筑方案，混凝土达到813 m3，横梁及桥面横向预应力较多，纵、横、竖三向管道布置密集、使得0号块梁端容易出现破坏。

墩顶0号块箱梁段作为整个上部结构悬臂施工的起点和基础，因其结构与受力复杂，施工工序环节多，施工条件限制较多，再加上0号块梁端具有梁体高、钢筋分布密集、悬臂高空作业及等诸多因素，造成施工中及成桥后0号块的应力分布极其复杂[1]。因此，应确保0号块梁端的施工质量和施工安全，避免0号块出现裂缝等影响结构安全的现象。由于0号块构造复杂，采用平截面假定的杆系计算模型无法对其受力状况进行准确的模拟，其计算结果仅能作为参考。建立局部精细化实体模型来反映结构的真实应力状况十分必要。

1 非线性有限元分析模型

1.1 模拟方法及单元选取

本文采用Abaqus 6.12进行建模计算，采用混凝土非线性损伤塑性模型的方法[2]。未考虑钢筋与混凝土及预应力筋与混凝土之间的“黏结-滑移”关系。钢筋和预应力钢筋采用分离式模型,即分别建立钢筋和预应力钢筋单元,然后采用Abaqus的Embedded约束方式与混凝土单元相连。

混凝土采用C3D10四面体二次单元，以消除剪力闭锁的影响[3]。预应力钢束及普通钢筋采用T2D2杆单元。单元基本尺寸取20 cm。为减小预应力钢束张拉引起的端部应力集中现象对横梁应力的影响，在横梁预应力端部建立锚垫板单元，锚垫板单元与混凝土采用Embedded的约束方式连接。根据圣维南原理，计算模型选取时除考虑0号块本身外，将其适当延长至2号节段。模型共划分为307 674个单元，49 176个节点。有限元网格见图3。

图3 有限元网格图

1.2 混凝土本构关系

采用混凝土非线性损伤塑性模型的方法来描述混凝土本构关系，用受压和受拉塑性应变的变化来表示破坏进展。该定义方法假设用混凝土的单轴受拉或者受压曲线来表示塑性损伤的特征，将损伤指标引入混凝土模型，对混凝土的弹性刚度矩阵加以折减，以模拟混凝土的卸载刚度随损伤增加而降低的特点。

混凝土应力-应变关系采用《混凝土结构设计规范》的推荐公式，其中为了求解的方便，将混凝土单轴受拉应力-应变关系进行了简化。混凝土单轴受拉时，到达峰值应力时对应的应变只有75×10-6～115×10-6，即受拉应力-应变曲线上升段非常短，本文为了求解方便而忽略上升段的影响，即在受拉应变为0时即认为混凝土受拉曲线对应应力为最大拉应力，及在前半部分认为是线弹性，损伤只发生在最大拉应力之后。

由于材料的工作过程就是不断损伤的过程，混凝土的破坏过程，实际上就是混凝土中损伤的形成和扩展累积直至完全损伤的过程，这个过程实际上在应力-应变关系中就得到了完整的反映。

混凝土单轴受拉塑性变化时损伤因子可根据单轴情况下的抗拉强度ft，抗压强度fc和弹性模量E0近似地推导得出。假设达到极限应力状况前，即在混凝土受拉曲线上升段没有损伤发生，即D=0，应力-应变关系为直线上升。达到极限应力后，即在曲线下降段，根据规范给出的应力-应变曲线关系，根据Sidoroff的能量等效原理，依次求出损伤因子D，在Abaqus里面只需输入开裂应变情况下的损伤因子D即可。

根据Sidoroff的能量等效原理，应力作用在受损材料产生的等效有损伤材料弹性余能

(1)

无损伤材料弹性余能的表达式为

(2)

由于有效应变σ′=σ(1-D)，于是可得Ed=E0(1-D)2，则进一步可以得到

σ=E0(1-D)2ε

(3)

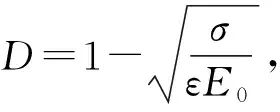
表1 C55混凝土随拉应变变化的损伤值

1.3 预应力钢绞线及普通钢筋本构关系

预应力钢绞线假设是弹性材料，钢绞线弹性模量取值为1.95×105MPa，极限强度标准值取值为1 860 MPa。钢筋假设是理想弹塑性材料，HRB335钢筋弹性模量取值为2.0×105MPa，屈服强度取值为335 MPa。HPB235钢筋弹性模量取值为2.1×105MPa，屈服强度取值为235 MPa。

1.4 加载方式

为观察破坏状况下的0号块的力学行为和破坏特征，采用0号块两端截面对称加载的模式来加载[4]。采用荷载控制的加载方式。由于集中荷载加载在塑性材料上会产生严重的应力集中现象，导致不收敛情况出现，因此在梁底支座处建立弹性模量与混凝土相同的弹性垫块，在加载截面形心位置设置关键点，该关键点与截面表面采用主从约束的方式连接[5]。

结构自重通过容重和重力加速度程序自动加载。二期恒载通过面力施加。

预应力根据实际的位置布置，根据整体计算模型读出扣除全部预应力损失并考虑使用阶段作用标准值引起的钢束应力变化后的预应力钢束的拉应力，通过反算后按降温法处理施加。边界力的作用力根据平面杆系有限元软件midas Civil 2012计算得到的截面内力(扣除0号块内钢束产生的钢束一次内力后)，在截面处施加轴力、剪力及弯矩[6]。本文最不利工况下内力值见表2。

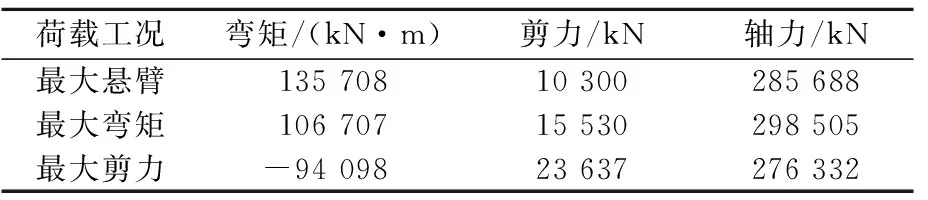
表2 不同荷载工况下的内力值

1.5 求解过程

混凝土结构由于材料非线性和几何非线性的影响，求解不收敛常常是有限元模拟的难点。非线性分析中，不能像线性问题通过求解单一系统的方程计算求解，而是增量地施加给定的荷载求解，逐步获得最终结果。在本文中，采用弧长法求解计算，在解决收敛问题时能够取得较好的效果，同时在计算中考虑了几何非线性效应。

2 分析结果

2.1 线弹性分析结果

根据表2中荷载工况对0号块进行计算，取3个荷载工况计算结果的最大值。图4、图5分别给出了不考虑材料非线性时0号块第一主应力和第三主应力云图。由图4、5可知，线性分析时应力集中现象较为明显，最大主应力图中拉应力值峰值为-8.15 MPa，压应力峰值为2.3 MPa。最小主应力图中，拉应力峰值为-1.57 MPa，压应力峰值为16.8 MPa。部分区域拉应力超过了C55混凝土标准抗拉强度-2.74 MPa的要求。

图4 线性分析最大主应力图

图5 线性分析最小主应力图

图6给出了不考虑材料非线性时0号块的真实性应变云图。应变最大为2.3×10-4，最小为-1.70×10-5。部分区域拉应变超过了C55混凝土单轴抗拉强度对应的峰值拉应变为1.1×10-4的要求。

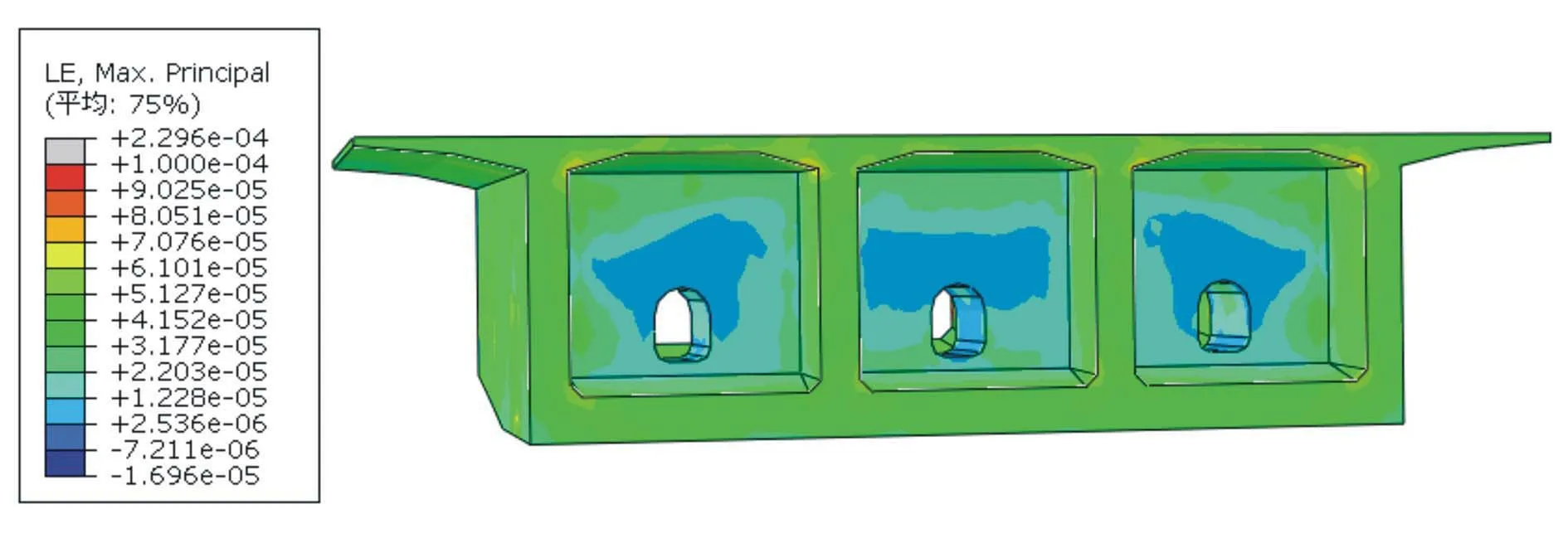
图6 线性分析对数应变图

由此可知，0号块部分区域材料进入了非线性状态，采用更进一步的非线性分析能更加真实地反映出受力结果。

2.2 非线性分析最大主应力结果

图7给出了考虑材料非线性的0号块的第一主应力云图。

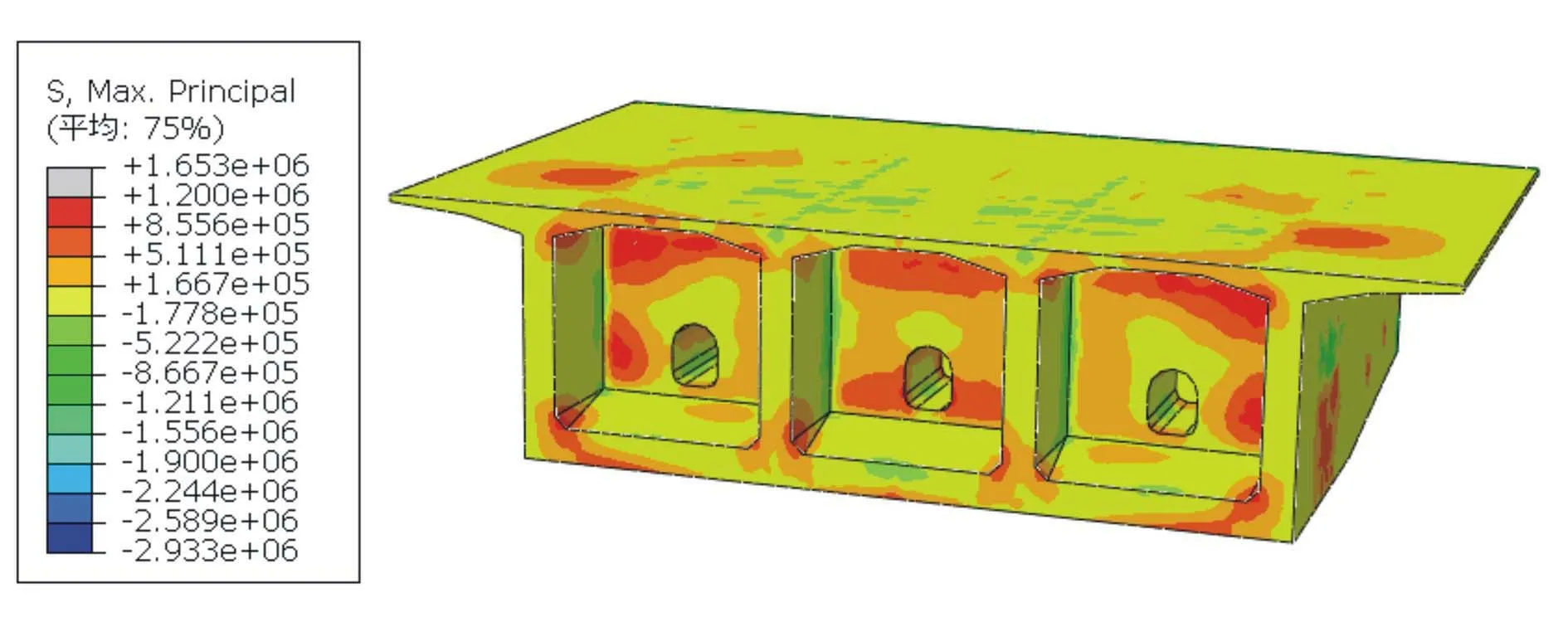
图7 非线性分析最大主应力图

由图7可见，除顶板与腹板倒角处由于应力集中产生较大拉应力以外，横梁范围内最大主拉应力出现在边腹板顶部，最大值达到1.2 MPa，这主要是由于纵向受力产生的正应力及箱梁支点处本身存在剪力滞效应所产生的。另外在边腹板内侧靠近顶板部位及人孔附近产生较大拉应力，最大值达到1.6 MPa，这主要是横梁支座外侧相当于悬臂梁(悬臂达7.5 m)，横梁需要配置较大预应力钢束，横向产生了较大弯矩和剪力所导致。设计及施工中应着重考虑该部位普通钢筋的配置。另外在腹板与顶底板倒角处、横梁横向钢筋锚固处，由于应力集中的作用,也存在拉应力,而实际该部位配置有锚垫板钢筋及锚后螺旋筋,实际应力经过发散后会较小。

2.3 非线性分析最小主应力结果

图8为非线性分析最小主应力图。

图8 非线性分析最小主应力图

由图8可见，从最小主应力云图可以得知，0号块基本都处于受压状态，压应力超过-12 MPa区域主要集中在靠近0号块底板变厚开始位置，顶板靠近横梁倒角部位也存在-9.1 MPa压应力。人孔周围由于存在部分拉应力，其值皆较小，不超过0.5 MPa，普通钢筋配置后该拉应力可满足规范要求。

2.4 非线性分析与线性分析应力结果对比

表3给出了线性与非线性分析的最大主应力结果对比。

表3 线弹性与非线性分析最大主应力值 MPa

根据表3分析结果对比可知，采用非线性分析时应变与主应力结果与线性分析结果存在一定的差异。结合图4和图7云图可知，采用非线性分析应力分布更为广泛，能消除部分应力集中现象，应力结果更为真实。

2.5 非线性分析应变结果

图9、图10分别给出了考虑材料非线性的0号块名义塑性应变和真实塑性应变云图。

图9 非线性分析塑性应变图

图10 非线性分析对数应变图

由图9、图10可见，0号块绝大部分区域处于弹性工作状态，仅在部分横梁与腹板倒角处、横梁与顶板倒角处、腹板与顶板倒角处及腹板下弯钢束锚固处由于应力集中存在塑性变形。塑性应变最大值达到4.84×10-4，最小为-1.65×10-5。根据对数应变云图可知，最大拉应变为5.35×10-5，小于混凝土极限拉应变1.00×10-4；最大压应变为-1.694×10-5，远小于混凝土峰值应变0.002，皆能满足规范要求。设计及施工中应着重考虑这些部位普通钢筋的配置及施工质量。

对比图10与图6应变结果可知：线性分析与非线性分析中应变分布情况基本一致，采用线性分析时，应变结果较小，最大为2.3×10-4，比非线性分析结果5.35×10-4小；最小为-1.70×10-5，与非线性分析结果基本一致。采用非线性分析时，应变结果考虑到塑性发展，拉应变值更为精确。

3 结论

1) 除去顶板与腹板倒角处由于应力集中产生的较大拉应力外，横梁范围内最大主拉应力出现在边腹板顶部，最大值达到1.2 MPa，这主要是由于纵向受力产生的正应力及箱梁支点处本身存在的剪力滞效应所产生的。另外在边腹板内侧靠近顶板部位及人孔附近产生较大拉应力，最大值达到1.6 MPa，这主要是由于横梁支座外侧相当于悬臂梁(悬臂达7.5 m)，横梁需要配置较大预应力钢束，横向产生了较大弯矩和剪力所导致。另外在腹板与顶底板倒角处、横梁横向钢腹板和顶板相交处主拉应力值较大。横梁人孔下缘主拉应力及压应力较大。

2) 从最小主应力云图可以得知，0号块基本都处于受压状态，压应力超过-12 MPa区域主要集中在靠近0号块底板变厚开始位置，顶板靠近横梁倒角部位也存在-9.1 MPa压应力。人孔周围由于存在部分拉应力，其值皆较小，不超过0.5 MPa。

3) 根据塑性应变云图可知，0号块绝大部分区域处于弹性工作状态，仅在部分横梁与腹板倒角处、横梁与顶板倒角处、腹板与顶板倒角处及腹板下弯钢束锚固处由于应力集中存在塑性变形。塑性应变皆能满足规范要求。

4) 通过对比线性分析与非线性分析结果可知，采用非线性分析时应变与主应力结果与线性分析结果存在一定的差异。采用非线性分析应力分布更为广泛,能消除部分应力集中现象，应力结果更为真实,应变结果考虑到塑性发展,拉应变值更为精确。

总之，在0号块设计时，对应力较大或出现塑性应变的部位，设计中应增加普通钢筋的配置，施工中应着重考虑这些部位的施工质量。