静定结构学与三角形的稳定性的来源及其表达

☉湖北省武汉科学技术馆 张忠斌

三角形的稳定性的来源可以追溯到静定结构学，其中有刚架、桁架、拱等结构，存在结构稳定性和结构不稳定性的论述；而在后来诸多结构力学中，所使用的术语是几何不变体系和几何可变体系.

本文结合静定结构学、早期几何、结构力学等相关内容，进行对比分析.或可让我们更深刻地了解有关三角形的稳定性的来源，以及早期表达，并审视其作为几何知识所存在的问题.

一、静定结构学中的结构稳定性

钱今希编1952年版《静定结构学》［1］有刚架、桁架等内容，摘录如下：

刚架——这类结构的组成杆件是相互刚接的，即各杆件在接端是不可能有任何相对移动和转动的意思.图1所示的连续梁和房架即是代表这类型的.

桁架——这类结构的杆件是相互铰接的，即各杆件的接端不能有相对的移动，但是在受荷重后结构发生形变时，杆件间的角度可以自由变动.图2表示几种常见的静定桁架.

图1

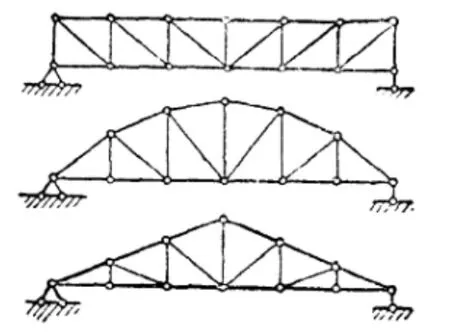
图2

稳定和不稳定——自由度每一个结构，在外力的作用之下，都会发生形变，这是因为它的各部杆件，在受力中发生了压缩、拉长或弯曲等应变的缘故.但是这些应变比起杆件原来的尺寸来是很微小的，所以结构的形变很小，不足以影响它的稳定.这种仅在杆件发生应变后才引起形变的结构是稳定的.

另外有些结构，在极微小的外力作用下，它就会发生很大的形变.形变的来源，不是因为各部杆件发生了应力和应变，而是结构本身组织的不健全的缘故，这就是不稳定结构.

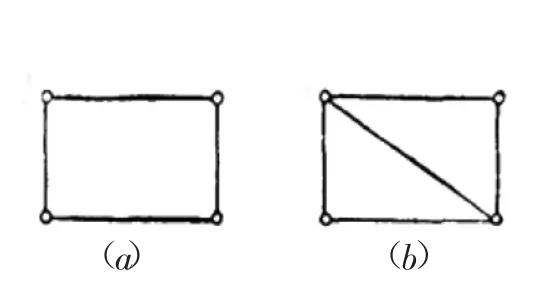
图3

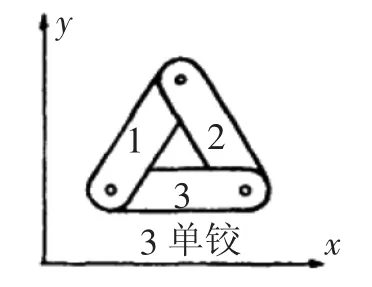
图4

图3（a）的结构是不稳定的.经过增加一根斜杆，如图3（b），便变成稳定的了.

又如三个构件用三个铰相互联结（如图4），总的自由度该是3×3-3×2=3.这和一个单构件的自由度相同，这说明铰接三角形本身是稳定的，这就是以后将叙述的桁架组织的基本原理.

该《静定结构学》介绍分析了刚架、桁架、稳定和不稳定等概念，并论述了桁架组织的基本原理“铰接三角形本身是稳定的”.但这个原理并不涉及刚架.从图1中可以看出局部为U型的房架是刚架，具有稳定性.U型刚架都具有稳定性，那么刚接四边形更具有稳定性.

二、三角形的稳定性的早期表达

对于三角形的稳定性，1960年的名称是三角形的坚固性（稳定性）、三角形具有固定性（即三角形的刚性），1972年的名称是三角形的稳定性.

1.彭乐元编著1960年版《平面几何与生产实践》［2］

当两三角形三边对应相等时，这两个三角形就全等.根据这个定理可以知道，当三角形的三边已知时，它的形状就被固定了.三角形的这种坚固性（稳定性）可以应用到起重机的移动臂（如图5）、桥梁及房屋架顶（如图6）上去……木栅栏门上所钉的一根斜木条也是利用了三角形的坚固性.

2.陕西省纺织工业局编1960年版《几何与三角教学参考资料》［3］

三角形具有固定性（即三角形的刚性），它在实际生活和生产中的应用是非常广泛的.例如：建筑上“人”字形的屋梁和桥梁结构等，都是应用了三角形的固定性，关于这部分，最好用三角形和四边形的架子，一面讲一面做实验.

3.成都电讯工程学院编1972年版《几何》［4］

当你们坐的椅子或凳子摇晃了，如果钉上一根木条，使椅腿和座板构成一个三角形（如图7），椅子就牢固了.你想过这里面的道理吗？这是因为只要三角形的三条边的长度固定了，这个三角形的形状和大小就完全确定了.这就是三角形所具有的稳定性.三角形的稳定性在工程技术和日常生活中应用很广，例如人字梯，只要用铁钩把梯子的两边连在一起，构成一个三角形，梯子就稳定不动.桥梁、屋架、吊架等多采用三角形结构，都是利用它的稳定性.容易看出，四边形就不具备稳定性，当四边形的四条边长固定时，四边形可以有各种不同的形状.

图5

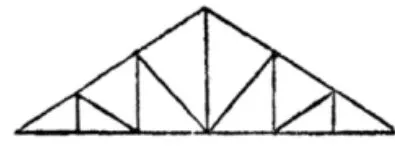
图6

图7

三、三角形的稳定性与结构稳定性的对比

上述这几本书都属于理工类的课本或教学参考，而书中“三角形所具有的稳定性”观点来源于《静定结构学》桁架组织的基本原理“铰接三角形本身是稳定的”；但前者存在两个比较突出的问题：

（1）《平面几何与生产实践》中有“三角形”，《几何与三角教学参考资料》中有“三角形和四边形的架子”，《几何》中有“四边形就不具备稳定性”.简单地用“三角形、四边形”替代“铰接三角形、铰接四边形”是否合理？

桁架组织的基本原理“铰接三角形本身是稳定的”，并不适用于钢架.除了“铰接”多边形之外，还应该有“刚接”多边形，那么刚接四边形具不具备稳定性呢？上述问题在几何中都没有讨论.

“三角形所具有的稳定性”、“四边形就不具备稳定性”分别等同于“铰接三角形本身是稳定的”、“图3（a）的结构是不稳定的”吗？显然，静定结构学只能得出它自己的结论.

（2）《平面几何与生产实践》中有“当两三角形三边对应相等时，这两个三角形就全等”，这就是三角形全等判定边边边公理；“根据这个定理可以知道，当三角形的三边已知时，它的形状就被固定了”，即是说“三角形的这种坚固性（稳定性）”的依据是边边边公理，但这与下文结构力学的“三角形规则”不相符.

作为几何的一个知识点，三角形的稳定性既没有设置铰接、刚接、铰接三角形和铰接四边形等概念，也没有作出其几何图形，因而出现概念混淆、逻辑混乱等问题，让人很难理解甚至被误导.遗憾地说，三角形的稳定性并没有建立良好的开端.

四、结构力学中的几何不变体系

刘金春主编2008年版《结构力学》［5］有几何不变体系、几何可变体系内容，摘录如下：

由梁和柱等直杆全部或部分采用刚性连接组合而成的结构，称为刚架（或框架）.刚架的形式很多，有单跨单层的，见图8.

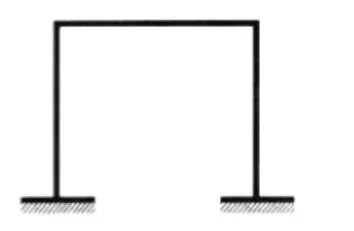
图8

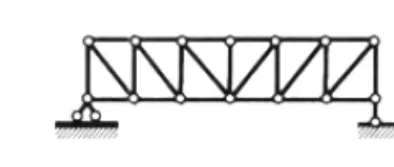
图9

仅在两端与铰结点相连的直杆，称为链杆.全部由链杆和铰结点组成的结构，称为桁架.当其支座性质与梁的支座相同时，称为梁式桁架，见图9.

图10（a）所示的是由两根杆件与地基组成的铰接三角形，当其受到任意荷载作用时，若不考虑材料的变形，则其几何形状与位置均能保持不变，称这样的体系为几何不变体系.而图10（b）所示铰接四边形，即使不考虑材料的变形，在很小的荷载作用下，也会发生机械运动而不能保持原有的几何形状和位置，这样的体系称为几何可变体系.一般工程结构都必须是几何不变体系，而不能采用几何可变体系，否则将不能承受任意荷载而维持平衡.

图10

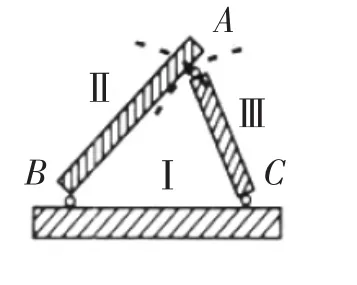
图11

图11所示的三个刚片Ⅰ、Ⅱ、Ⅲ由B、A、C三个单铰两两相联.假定刚片Ⅰ不动，我们来研究各刚片之间相对运动的可能性.由于刚片Ⅱ与刚片Ⅰ用铰B相联，故刚片Ⅱ只能绕铰B转动，其上A点的运动轨迹是以B为圆心，以AB为半径的圆弧；而刚片Ⅲ与刚片Ⅰ用铰C相联，刚片Ⅲ只能绕C点转动，其上A点的运动轨迹是以C为圆心，以AC为半径的圆弧.而实际上刚片Ⅱ、Ⅲ是用铰A相联结的，A点既是刚片Ⅱ上的点，也是刚片Ⅲ上的点，它不可能同时沿两个方向不同的圆弧运动，只能在两个圆弧的交点处固定不动.于是各刚片间不可能发生任何相对运动，故该体系是几何不变的，且无多余联系.

……

平面几何不变无多余约束体系的组成规则有三个：

①三刚片规则：三刚片用不在一直线上的三个铰两两相联.

②二刚片规则：两刚片用一个铰和一根不通过此铰的链杆或三个既不全平行也不交于一点的三根链杆相联结.

③二元体规则：在一个体系上增加一个二元体或拆除一个二元体，不改其几何不变性.

三个规则的实质是三角形规则，即三角形的三个边长一定，其几何图形是唯一确定的.

……

刚架和桁架都是由直杆组成的结构，两者的区别是：桁架中的结点全部都是铰结点，刚架中的结点全部或部分是刚结点.图12（a）是一个几何可变的铰结体系，为了使它成为几何不变体系，一种办法是增设斜杆，使它成为桁架结构（图12（b）），另一种办法是把原来的铰结点B和C改为刚结点，使它成为刚架结构（图12（c））.由此看出，刚架中由于具有刚结点，因而不用斜杆也可组成几何不变体系，使结构内部具有较大的空间，便于使用.

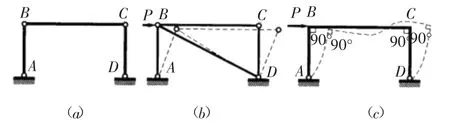
图12

与铰结点相比，刚结点具有不同的特点.从变形角度来看，在刚结点处各杆不能发生相对转动，因而各杆间的夹角始终保持不变，如图12（c）中虚线所示.

对该《结构力学》的上述内容进行分析：

（1）从几何的角度看，该书的一大亮点是论述了“三角形规则”，即“三角形的三个边长一定，其几何图形是唯一确定的”.这是三角形的确定性命题［6］. 显然，结构力学中的几何不变体系的三角形规则一直在寻求几何依据.

（2）图11是三刚片规则的论证过程，其描述与几何作图题“给定三边作三角形，所作的三角形是唯一的”如出一辙.

（3）图8单跨单层刚架看起来像U型结构，是几何不变体系.

（4）若连接图12中的A、D两点，则图12（c）可看作将图12（a）的铰结四边形桁架改造成刚结四边形刚架；那么图12（c）是刚结四边形，是几何不变体系.

（5）“刚架和桁架都是由直杆组成的结构……刚架中的结点全部或部分是刚结点”，在理论上预示了刚结四边形的存在.设若四边形的四个结点都是刚结点，那么这个刚结四边形是几何不变体系.

五、结束语

几何作图可以看作数学上的理想实验.有这样一类几何作图题，即仅给定合适的边长而不给定角度作多边形，所作的三角形只有唯一一个，而四边形、五边形等则不是唯一一个.因而有三角形的确定性的一个结论：给定三边，则三角形唯一确定.这就是结构力学中的三角形规则.另外还有四边形的一个不确定性结论：给定四边，四边形不能唯一确定.

笔者不久前提出链式多边形［7］，并几何作图链式三角形和链式四边形.只是对应于几何不变体系，三角形的稳定性应该更名为链式三角形的不变性或铰结三角形的不变性.