一道中考几何压轴题的解法探究
2018-10-11重庆市万州高级中学
☉重庆市万州高级中学 张 进
综合运用线段垂直平分线的性质和判定、等腰三角形的性质和判定、全等三角形的判定和性质、平行四边形(矩形、菱形、正方形)的判定和性质、勾股定理及其逆定理、特殊角的三角函数值等知识的几何综合题是历年来重庆中考的热点题型,这类试题需要添设适当的辅助线方能使问题得到解决,备受一线教师的关注与研究.以重庆2018年中考B卷压轴题(第24题)为例,笔者在中考结束后,为八年级学生提供该题作为一道课外作业试题,让学生尝试不同的证明方法,并从多种解答方法中阐述自然解法的生成.
一、题目与解析
如图1,在平行四边形ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA.BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.
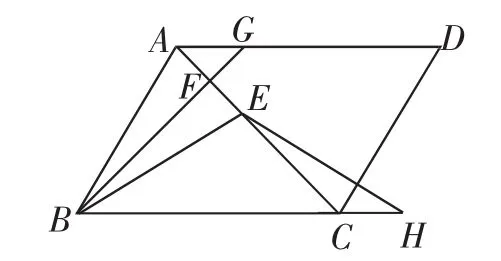
图1


(2)证法1:如图2,连接GE、GH.因为BF⊥AC于点F,BE=BA,所以∠ABF=∠EBF.又因为GB=GB,所以△ABG△EBG(SAS),所以∠AGB=∠EGB.因为在Rt△FBC中,∠ACB=45°,所以∠FBC=45°.因为AD∥BC,所以∠GAC=∠ACB=45°,∠AGB=∠FBC=45°.则∠EGB=45°.因为CH=AG,所以四边形ACHG是平行四边形,所以∠GHC=∠ACB=∠GBH=45°,GB=GH,∠BGH=90°,所以∠BGE=∠HGE=45°.因为GE=GE,所以△GBE △GHE(SAS),所以EB=EH.(以上为命题者提供的参考答案)
二、第⑵小题多解思路简析(解法探究)
笔者对该试题讲评时,师生一起深度挖掘载体图形中的基本图形和基本题设条件,认真挖掘命题者给出的解题思路,探寻不同的解题思路,花费一节课的时间让学生不断提及不同的解决方式,借助学生的发散思维,将这些问题解决的方式一并呈现:
证法2:如图3,过点E作EK∥BC交BG于点K.先证△AFG △EFK(ASA)且都为等腰直角三角形,所以AG=EK=CH,因为△FBC是等腰直角三角形,所以BK=EC,再证△BKE △ECH(SAS)即可.

图3

图4
证法3:如图4,过点A作AK⊥AD交BG于K.先证△AGK是等腰直角三角形.因为BF⊥AC,所以AF=FK=FE,因为△FBC是等腰直角三角形,所以BK=EC.再证△BKA△ECH(SAS)即可.
证法4:如图5,过点H作HK⊥AC交AC的延长线于K.先证△AFG△HKC(ASA)且都为等腰直角三角形,得到AF=EF=CK=HK.因为△FBC是等腰直角三角形,所以BF=CF=CE+EF=CE+CK=EK.再证△BAF△EHK(SAS)即可.
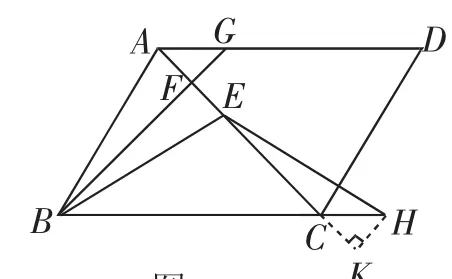
图5

图6
证法5:如图6,过点E作EK⊥AC交BC于K,过点B作BM⊥EK交EK的延长线于M.可先证△AFG△BMK(ASA)且都为等腰直角三角形,得到BK=AG.然后证四边形BMEF是矩形,则EM=BF=CF.因为MK=BM=EF,所以EK=EC.最后证△EKB△ECH(SAS)即可.
证法6:如图7,过点H作HK⊥BC交AC的延长线于K.先证△AFG和△CHK均为等腰直角三角形,得到HK=CH=AG. 再证CK=2EF,BG=BF+FG=CF+AF=CE+2EF=EC+CK=EK.最后证△BAG△EHK(SAS)即可.
证法7:如图8,过点E作EK⊥AC交BC于K,过点B作BM⊥BK交EK的延长线于M.因为BF⊥AC,所以EM∥BG,则∠BEM=∠EBF=∠ABG.易证△BKM是等腰直角三角形,所以△BAG△EBM(AAS),则AG=BM=BK=CH.最后证△EKB △ECH(SAS)即可.

图7

图8
证法8:如图9,延长FG至K,使KF=BF,连接AK.可证△BEF △KAF(SAS),得到AK=EB.易证△AFG和△BFC是等腰直角三角形,则KG=KF-FG=BF-EF=CF-EF=EC.最后证明△ECH △KGA(SAS)即可.

图9
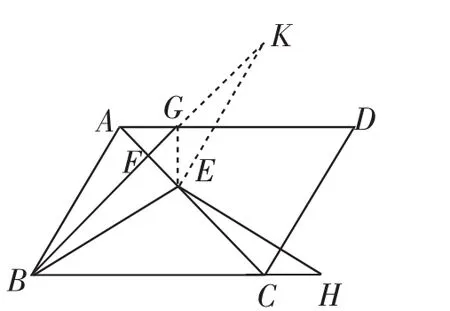
图10
证法9:如图10,延长FG至K,使KF=BF,连接EG、EK.先证△BAF △KEF(SAS),得到EK=AB=EB.再证△AEG、△EFG、△BFC是等腰直角三角形,则GE=AG=CH.易证KG=KF-GF=BF-EF=CF-EF=EC.然后证△KGE △ECH(SAS)即可.
证法10:如图11,连接EG、CG.先证△AFG、△AEG、△BFC是等腰直角三角形.再证△BAG△CGA(SAS),得到BA=CG.然后证△CEG △ECH(SAS),即可证得EH=CG=BA=BE.

图11

图12
证法11:如图12,过点E作EK⊥AC交BC于K,连接EG、KG.先证△AEG、△EFG、△BFC是等腰直角三角形.再证△EKG△KEB(AAS),得到KG=EB=AB,BK=EG=AG.再证△ECHEKB(SAS),则EB=EH.
证法12:如图13,过点E作EK⊥AC交BC于K,交AD于M.先证四边形BKMG是平行四边形.再证FG是△AEM的中位线,得到AG=GM=BK.因为△CEK是等腰直角三角形,可证△EKB△ECH(SAS),则EB=EH.
证法13:如图14,过点E作EM∥AD交BG于M,过点E作EN∥BG交AD于N.可得四边形MENG是平行四边形.又FG是△AEN的中位线,则AG=EM=CH,最后证明
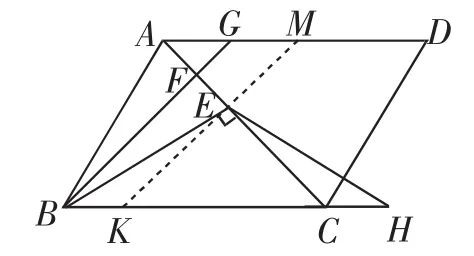
图13

图14
上述解法不失为参考答案之外的精彩解答.在解题教学中开展一题多解是杜绝“题海战术”的有效手段.对于一个题目,给学生提供多种解法,从不同的角度去看待一个问题,用多重视角反思一个问题,这就是在增加学生的思维层次,这与“培养学生核心素养”提出的“学会学习,勤于反思”不谋而合.相信通过“一题多解”可以初步提高学生学习数学的兴趣,能够为引导学生发现题目之“美”打下一定的基础.
下面展示学生提供的不同解法,有的解法复杂甚至烦琐,但学生对数学问题多种解法的不懈追求,却体现了数学思维的深刻性、发散性、变通性、灵活性、流畅性和开放性.
证法14:如图15,过点A作AK⊥AD交BG于K,连接EK,以下过程同证法3.

图15
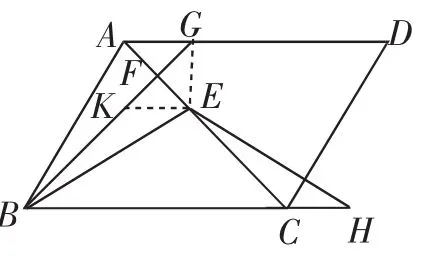
图16
证法15:如图16,过点E作EK∥BC交BG于点K,连接EG,以下过程同证法2.
证法16:如图17,过点A作AM⊥BC交BG于K,连接EK,以下过程同证法2.

图17

图18
证法17:如图18,过点G作GM⊥BC于点M,EK∥BC交BG于K,连接EK,以下过程同证法3.
证法18:如图19,过点E作EK∥BC交BG于点K,连接EG、AK,以下过程同证法16、17.

图19
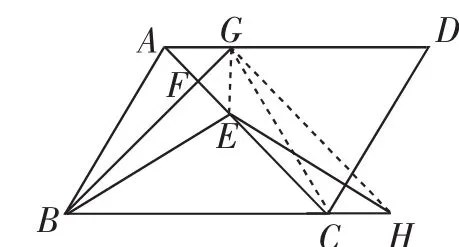
图20
证法19:如图20,连接EG、CG、GH,以下过程同证法1.
证法20:如图21,过点A作AK⊥BC于点K,交BG于N,过点E作EM⊥BC于点M,以下过程同证法3.
证法21:如图22,连接EG并延长GE交BC于K,连接CG,以下过程同证法10.
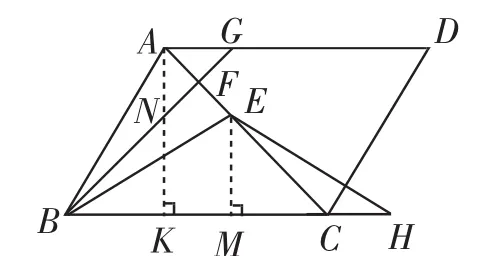
图21

图22
证法22:如图23,连接EG并延长GE交BC于K,连接HG,以下过程同证法1.
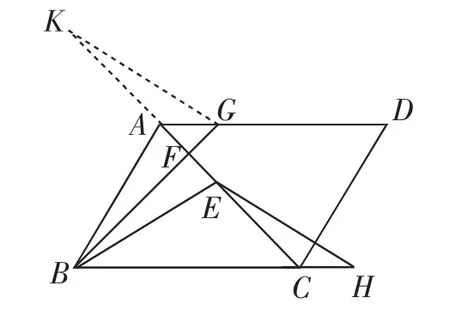
图24

图23
证法23:如图24,延长FA至K,使AK=EC,连接GK.先证△AFG、△BFC是等腰直角三角形.再证△KFG△BFE(SAS).最后证明△KAG △ECH(SAS)即可.
三、解题反思
几何问题的解答方法很多,但只要能找到解题规律,任何难题都可以迎刃而解.教师在解题教学中要善于引导学生挖掘题目中的隐含条件,从复杂的图形中分解或构造出基本模型图,善于提炼基本几何模型,进行归纳总结.利用建模思想解题,既可以培养学生应用模型的意识,提高学习数学的兴趣,又可以培养学生知识迁移应用的能力,所以在数学学习过程中,要不断寻求新的解题方法,逐步提高自己的解题技能和技巧,以达到举一反三、触类旁通的学习效果.
在平时的教学过程中,教师可通过对一些典型考题的几何图形进行挖掘,借助知识经验和思想方法,在直观视觉和比较分析的基础上,添加适当的辅助线解决问题,加强解题经验和方法的总结,如解决复杂几何问题常用辅助线的作法:连接线段,延长线段,过一点作平行线,过一点作垂线,作辅助图形(圆、特殊四边形、三角形等),要加强学生思维的拓展训练,引导学生结合题目特点进行一题多解,一题多变,一图多用,拓宽思路,帮助学生在解题训练中发展思维的灵活性与发散性,让一题多解成就精彩,大大拓展学生的思维空间,使学生明白平面几何问题辅助线添加的多角度性、尝试的重要性,以及从多个视角的解决中获得平面几何问题思考的有效性,真正让解题教学的课堂更加高效、灵动.
