不忘本真 方得自然——例谈借助问题的联系性、连续性自然解导数解答题及感悟

安徽省宿州市宿城第一中学 (234000)

吴 跃

导数是高考和各省市模拟考试考查的重要知识，文、理科往往都将导数作为试卷的压轴题进行考查，体现了导数在选拔性考试中的把关功能.本文从近期出现的模拟题、高考题出发，借助问题的联系性、连续性解决导数的压轴题的同时谈一谈解法自然的生成，以此来加强学生核心素养的培养.

一、例题分析

1.题目逻辑的本真

例1 (华大新高考联盟2018届质量测评)

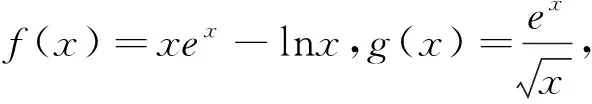
2.71828…是自然对数的底数.

(1)讨论g(x)的单调性；

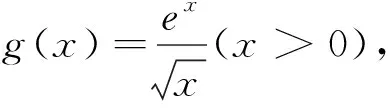
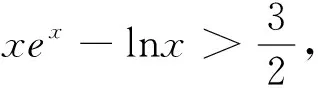
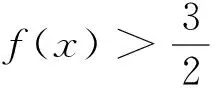
2.题目预设的本真

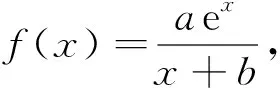
(1)求a,b的值；

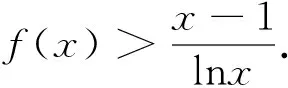
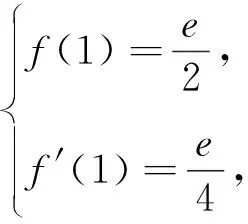
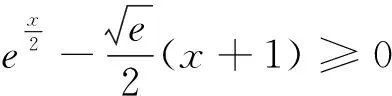
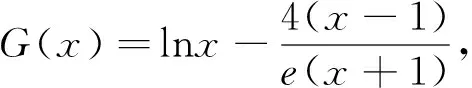
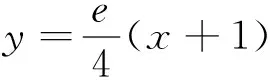
3.中间结果的本真

例3 (2017高考全国卷Ⅰ)已知函数f(x)=ex(ex-a)-a2x.

(1)讨论f(x)的单调性；

(2)若f(x)≥0，求a的取值范围.

解析：(略)

点评：第(1)问通过分类讨论的方法，分a>0,a<0,a=0三种情况，求出函数f(x)单调区间.第(2)问在(1)的延续下，根据单调性，在三种情况下考虑函数f(x)的最小值，解不等式f(x)min≥0即可.本题的两个问题衔接的非常自然、流畅，这种利用解题的中间结果解决下一问题的方法当然体现解法自然.利用中间结果解题的试题在各省市高考中比较常见，当然呈现形式也多种多样，比如有的试题第(1)问求出参数范围，在第(2)问只需取参数的一个特殊值，问题迎刃而解.

二、反思

1.把握问题本真 探究解法自然

数学家、数学教育家乔治·波利亚在《怎样解题》一书中阐述了他的“怎样解题表”解题理论，该理论体现了他对解法自然的理解：你是否利用了所有的已知数据?你是否利用了整个条件?你是否考虑了包含在问题中的必要的概念?

国内对解法自然的理解标准不一，罗增儒教授在《数学解题学引论》中指出：解答数学习题的实质是：“解数学题，这就是要找到一种一般数学原理(定义、公理、定理、定律、公式)的序列，把这些原理用于习题的条件或者条件的推论(解题的中间结果)，得到习题所要的东西，即习题的答案.”

通过两位教育专家对解法自然的理解，不难看出把握问题本质、剖析试题的内涵，是解法自然的生成源头.解题时是否理解题干条件，有没有利用好解题的中间结果，是成功关键.命题者在命题时就会考虑问题的联系性、连续性，在学生的最近发展区设置问题.通过上述几个导数题的解答，在解题时围绕着解题成功的关键点展开，那么这种解法便行云流水、自然天成，就是我们追求的解法自然.

2.培养核心素养 探索学会学习

《教育部关于全面深化课程改革落实立德树人根本任务的意见》颁布后，中国学生发展核心素养的培养成为数学教育的一项基本任务，在数学活动中最重要的教学是教会学生学会学习，最重要的学习是学会学习.培养学生核心素养，应从学会学习出发，怎样培养学生学会学习的能力，是广大教育工作者正积极探索的问题.笔者认为，如果从以下几个方面出发，对学生学会学习能力的培养是有利的.

数学教学要自然，不强加于学生.叶澜教授说过：“教师的课堂教学要五实：扎实、充实、丰实、平实、真实.”这其实就是课堂教学最本真、最自然的体现.数学教学的自然有利于培养学生数学学习兴趣，促使乐学善学.

数学命题要自然，不拼接乱造.科学设计命题内容，在考查形式和内容上要自然，体现引导教学和服务选才的功能.数学题目的命制除了重视对基础知识、基本技能的考查，还要着重考查学生独立思考和运用所学知识分析问题、解决问题的能力，培养学生勤于思考、善于思考的意识.

学生习惯要自然，不强制约束.教育家叶圣陶先生说过：“教育就是习惯的培养.”

英国著名哲学家培根也说过：“习惯真是一种顽强而巨大的力量，它可以主宰人生.”由此可见习惯的重要性.培养学生学会学习的能力，就要使学生有一个好的习惯.自然生成的习惯有利于学生把学习当成自己的事情，主动探索适合自己的学习方法，养成良好的学习习惯，树立终身学习的意识.

3.培养质疑精神 提升创新能力

说到“质疑精神”，著名主持人杨澜举过她在哥伦比亚大学读研究生时候的一个例子.她选修了一门课是社会学，杨澜上课从不缺勤，作业认真完成，论文也写得不错，但期末考成绩公布时，杨澜所有科目的成绩都是A，唯独社会学是B.当时，不服气的杨澜立马去找教授“讨说法”，没想到，教授回答说：“给你B是为了惩罚你，因为你上课从来不提问，提不出问题的学生不是好学生.”

我国教育要适应世界教育改革发展趋势、提升国际竞争力，学生应该具备批判质疑精神，具有问题意识，具有独立思考、独立判断的能力[1].爱因斯坦说过：“提出一个问题比解决一个问题更重要，没有质疑的精神，就不会创新能力的提升.”习近平总书记在党的十八届五中全会第二次全体会议上的讲话中说道：“创新能力不强是我国发展的阿喀琉斯之踵.”在同首都各界群众和青少年一起参加全国科普日活动时，要求全社会大力弘扬创新精神、提高创新能力.作为一线教师，我们要善于鼓励、善于保护学生的质疑精神，在提升学生创新能力的道路上保驾护航.

三、结束语

纵观近几年的高考导数题，我们能发现，试题的命制都严格遵循《课程标准》和《考试大纲》的能力要求，紧扣“必备知识、关键能力、学科素养、核心价值”四层考查内容以及“基础性、综合性、应用性、创新性”四个方面的考查要求，凸显高考试题科学性、逻辑性、联系性、连续性.在解题的过程中要时刻注重试题本源，考虑问题的联系性、连续性，不忘本真，方得自然.