基于滑动时域窗和ERA的模态阻尼比辨识技术研究
2018-10-11蔡毅鹏周国峰南宫自军
王 亮,张 妍, 蔡毅鹏,周国峰,南宫自军
(中国运载火箭技术研究院, 北京 100076)
航天工程中,为了对载荷计算、姿态控制设计、动响应分析,以及惯性测量组合的安放位置提供参考,需要精确预示战术导弹的结构动力学特性。在设计时,一般先使用理论计算,再通过有限状态的模态试验结果对理论模型进行修正,最后使用修正的理论模型计算各状态下的模态特性。而地面试验无法完全模拟飞行状态,如外部的气动力和发动机的推力等。因此,基于遥测数据,采用环境激励模态辨识技术对飞行过程中的结构模态参数进行辨识,对验证设计参数非常重要。
环境激励模态辨识技术是将互相关函数同传统时域模态分析法相结合的方法,将响应之间的互相关函数代替传统时域模态分析法中的自由振动响应或脉冲响应函数。该方法不需要测量激励型号,而仅依靠各通道的时域响应数据进行系统的模态辨识。
环境激励模态辨识技术研究最早可以追溯到1968年cole的单阶模态测试的随机减量法[1]。1973年Ibrahim提出了一种参数识别的方法,该方法仅利用时域信号即可进行识别工作,经多年的不断完善形成了独具一格的Ibrahim时域法(ITD法)。国内外在模态参数识别研究在许多理论和应用中也取得了较多的成果[2-6]。其中练继建等[7]对基于熵降噪的水工结构振动模态特征系统实现算法(Eigensystem Realization Algorithm,ERA)进行了研究。刘兴汉等[6]对改进的随机子空间法进行了研究。徐亚兰等[7]分析了在众多小波基函数中 Morlet 小波更适合对动态结构系统进行模态分析,结合Morlet 小波的性质和结构系统对脉冲响应信号的特性,构造了一小波族,利用 Morlet 小波变换对多自由度系统进行模态解耦和对时变系统进行模态参数辨识。算例的数值仿真结果表明文中方法的正确性和有效性。王彤等[8]提出了一种基于频域空间域分解(Frequency and Spatial Domain Decomposition,FSDD)的工作模态分析方法。该法将同时具有输入和输出的试验模态分析的经典方法——复模态指示因子(Complex Mode In-dicator Function,CMIF)法拓展到了仅有输出响应的运行状态模态分析。FSDD法采用奇异值分解将信号空间和噪声空间分离,把奇异值曲线作为模态指示的依据,以奇异值向量作为加权函数得到每一阶模态的增强功率谱(Power Spectrum Density,PSD),进而在频域内对增强PSD曲线进行最小二乘拟合得到准确的模态频率和阻尼参数。黄琴等[9]提出并实现了一种基于随机减量技术和复模态指示因子函数法的新型频域运行状态模态参数识别方法。由随机运行响应估计随机减量函数,然后通过时频域变换得到频域的半功率谱密度函数,并用复模态指示因子函数法从半功率谱密度函数中识别结构模态参数。最后对一个三维空间结构模型进行算法验证,得到相应的各阶模态参数,证明了将随机减量技术和复模态指示因子函数法相结合的方法识别大型结构模态参数的有效性和合理性。
在使用环境激励进行模态辨识时,模态阻尼比辨识结果往往散布较大,其随辨识信号长度和不同信号段的影响较大。针对时不变系统,本文提出了采用带重复宽度的时域滑动窗口与统计方法结合的模态阻尼比辨识方法,提高模态阻尼比的辨识精度和稳定性。
1 模态辨识技术
ERA法属于一种多输入多输出的时域整体模态参数辨识方法。原理是利用实测的脉冲响应数据或自由相应数据构造Hankel矩阵,采用奇异值分解的方法,求得系统的特征值与特征向量,从而求得模态参数。该方法由于使用了现代控制理论中的最小实现原理,使得计算量大大减小,精度高,是目前最完善、最先进的模态参数辨识方法之一。
对于n维线性系统,当振动系统响应采用加速度传感器测量时,振动方程用向量可表示为
(1)
设离散时间点为k=0,1,2,…,采样时间间隔为Δt,则t=t0+kΔt,由零阶保持器的性质,在一个采样间隔内保持采样值不变,由此可得
Bf[(k+1)Δt]
(2)
Z变换形式的传递函数为
(3)
变换后可得传递函数
H(z)=z-2GA2(I-z-1A1)-1B1+z-1GB2+GB
(4)
整理后有
(5)
构造Hankel矩阵
H(k-1)=
(6)
整理得
(7)
令k=1,对H(0)做奇异值分解
H(0)=U∑VT
(8)
可推导出
(9)
设系统矩阵A的特征值矩阵(谱矩阵)为Λ,特征矢量矩阵为ψ′,则有
ψ-1Aψ=Λ
(10)
由指数矩阵的性质有
A1=eψΛψ-1Δt=ψeΛΔtψ-1,即ψ-1A1ψ=eΛΔt
从而知A1的特征矢量与A的相同,A1的特征值矩阵为
Z=eΛΔt=diag(z1,z2,…,z2n)
(11)
式(11)中Z的对角矩阵元素为zi=eλiΔt,i=1,2,…,2n;A的特征值矩阵Λ=diag(λ1,λ2,…,λ2n),且
(12)
由此可确定各个模态振动的固有频率、阻尼比和模态矩阵
固有频率
阻尼比
模态矩阵
Φ=Gψ
2 辨识技术实施流程
针对模态阻尼比辨识结果影响因素多,且辨识结果不稳定的问题,本文提出了采用时域滑动窗口与统计方法结合的模态阻尼比辨识方法,提高模态阻尼比的辨识精度和稳定性,图1给出了辨识方法的流程图。其中对原始信号进行功率谱密度分析,选择带辨识频带,对信号进行局部带通滤波后,使用选定宽度的时域矩形窗截取信号,对截取信号进行ERA方法下的模态辨识,并按给定重合宽度进行窗口滑动,从而获得各窗口对应的模态辨识结果,包括模态频率、阻尼比和振型,再对辨识结果按经验阻尼比范围及可能模态频率位置进行筛选,对通过筛选的模态阻尼比进行统计分析,取其均值作为最终辨识结果。
在使用滑动窗口时,需要指定窗口宽度,为了研究可有效辨识出模态数据长度的需求,采用ERA方法进行模态辨识时,数据的长度最有可能需要包含所需识别模态的6~8周期,为了有效利用信号的信息,本文采用8个周期数据长度作为窗口宽度进行辨识研究。
3 算例
3.1 悬臂梁模型介绍
算例计算时,对悬臂梁悬臂端进行白噪声激励,将各处加速度响应作为输入进行工作模态辨识。悬臂梁模型如图2所示,各参数如表1。
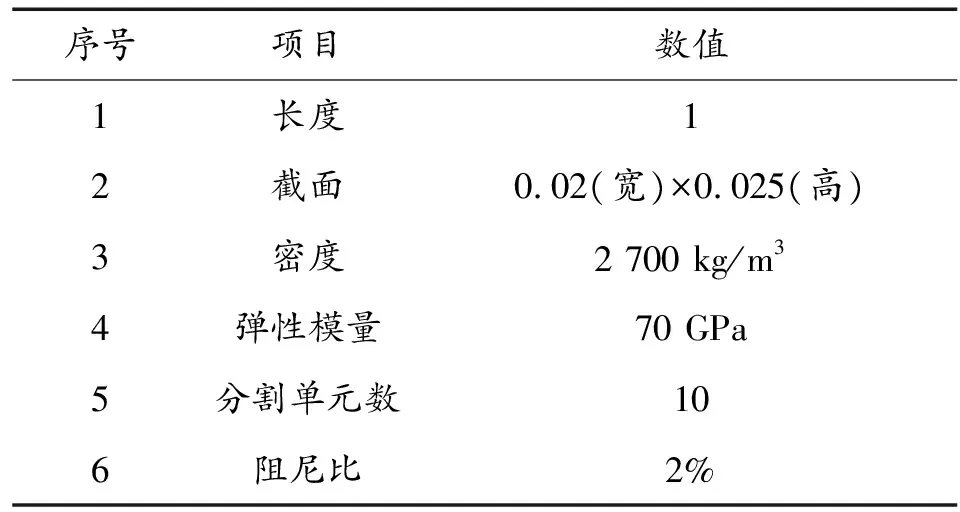
序号项目数值1长度12截面0.02(宽)×0.025(高)3密度2 700 kg/m34弹性模量70 GPa5分割单元数106阻尼比2%
采用wilson-θ方法用800 Hz频带白噪声进行激励悬臂梁端部,激励的时域信号如图3所示,典型位置响应如图4所示,图4为悬臂梁端部加速度时域响应。功率谱密度分析结果和原点加速度频率响应函数曲线分别如图5和图6所示。
3.2 单帧数据模态辨识
首先,仅采用对一段数据进行分析,辨识其模态,选择不用的数据长度,从待辨识模态所在频段内最低频率对于周期的8倍、10倍、15倍、20倍、25倍不等,分别采用ERA模态辨识方法进行模态辨识,信号内所包含的两阶模态的辨识结果如表2所示。从辨识结果可以发现,选择不同长度和位置的数据,利用其辨识的模态频率结果较为一致,散布较小,而对于不同模态阻尼比的辨识结果散布较大,最大和最小辨识值差别可达4倍。
因此,对于提高模态阻尼比的辨识稳定性及鲁棒性意义重大。
3.3 不同数据重合宽度对辨识结果的影响
在采用模态阻尼比辨识方法,本小节对比不同重合窗口宽度对辨识结果的影响,这里对比了重合宽度为4个周期、5.5个周期和7个周期3种情况,辨识结果如表3所示。一阶和二阶模态振型拟合结果如图6和图7所示,图8给出了典型的滑动窗口后阻尼辨识结果及统计情况,为6周期宽度的时域滑动窗口二阶模态阻尼比辨识结果。

表2 不同数据长度的模态辨识结果

表3 不同重合长度数据的模态辨识结果
使用不同重合宽度的时域窗口辨识模态时,从辨识结果可以得出以下结论:
1) 各阶模态频率辨识结果一致性较好,模态振型辨识结果良好,与理论计算结果较为一致;
2) 各阶模态阻尼比与理论值有一定的偏差,当时域窗口的重合宽度变大时,对于相同长度的信号,其可辨识次数较大,样本数目较大,因此对模态阻尼比辨识结果取均值后,结果更加接近理论值。
3.4 辨识算法对信号信噪比的鲁棒性
根据以上分析,本小节选择滑动窗口重合长度为7个周期,研究增加不同量级噪声对辨识结果的影响。这里对比了噪声量级从信号标准差的0、15%、30%、50%周期4种情况,辨识结果如表4所示。
对各节点数据同时增加不同噪声量级辨识模态时,从辨识结果可以得出以下结论:
1) 各阶模态频率辨识结果一致性较好,模态振型辨识结果良好,与理论计算结果较为一致;
2) 增加噪声后,对模态阻尼比辨识结果取均值,各阶模态阻尼比与理论值有一定的偏差,但偏差最大为20%左右,随着噪声量级,阻尼比辨识结果比较稳定,没有出现辨识结果偏差明显变大的情况,说明本文的方法对信号信噪比的鲁棒性较强。
3.5 辨识算法对信号信息量的鲁棒性
根据以上分析,本小节选择滑动窗口重合长度为7个周期,研究选择不同位置响应组合对辨识结果的影响。这里共选择4组组合,分别如下:
工况1:图2中1~10号梁单元右端平动响应;
工况2:图2中2、4、6、8、10梁单元右端平动响应;
工况3:图2中1、2、3、4、5梁单元右端平动响应;
工况4:图2中6、7、8、9、10梁单元右端平动响应;
其中,工况1代表了梁单元所有节点的平动响应,信息最为全面,工况2为从悬臂约束端到自由端较为稀疏但均匀分布节点的平动响应,工况3和工况4为接近约束端的节点组合和接近自由端的节点组合,显然工况3整体响应量级较工况4小。4种工况的辨识结果如表5所示。

表4 不同信噪比的模态辨识结果

表5 不同节点响应组合的模态辨识结果
对不同节点响应组合进行辨识模态时,从辨识结果可以得出以下结论:
1) 各阶模态频率辨识结果一致性较好,模态振型辨识结果良好,与理论计算结果较为一致;
2) 不同的节点响应组合下,对模态阻尼比辨识结果取均值,模态阻尼比的辨识结果较为一致,与理论值最大偏差在10%左右,说明本文的方法对信号的通道数量的鲁棒性较强。
4 结论
各阶模态频率辨识结果一致性较好,模态振型辨识结果良好,与理论计算结果较为一致;各阶模态阻尼比与理论值有一定的偏差,当时域窗口的重合宽度变大时,相同长度的信号,其可辨识次数较大,样本数目较大,对模态阻尼比辨识结果取均值后,结果更加接近理论值;各阶模态频率辨识结果一致性较好,模态振型辨识结果良好,与理论计算结果较为一致;增加噪声后,对模态阻尼比辨识结果取均值,各阶模态阻尼比与理论值有一定的偏差,但偏差最大为20%左右,随着噪声量级,阻尼比辨识结果比较稳定,没有出现辨识结果偏差明显变大的情况,说明本文的方法对信号的信噪比的鲁棒性较强;各阶模态频率辨识结果一致性较好,模态振型辨识结果良好,与理论计算结果较为一致;不同的节点响应组合下,对模态阻尼比辨识结果取均值,模态阻尼比的辨识结果较为一致,与理论值最大偏差在10%左右,说明本文的方法对信号的通道数量的鲁棒性较强。
