考虑两端换流器影响的直流输电系统谐波不稳定风险评估

卢智雪, 刘天琪, 陈 相, 何 川, 陶 艳

(四川大学电气信息学院, 四川省成都市 610065)

0 引言

高压直流(high voltage direct current,HVDC)输电系统因输送容量大、距离远、损耗低等优点而被广泛投入使用[1-2],但系统中的发电机、直流输电线路由于其固有的阻抗频率特性,在运行过程中容易发生感容耦合;换流器为非线性元件,在运行过程中相当于谐波源,会产生大量的谐波;换流变压器铁芯饱和使得谐波通过换流器在交直流系统间相互调制后,可能会导致谐波放大,甚至会造成系统崩溃[3-4]。因此,有必要深入研究HVDC输电系统的谐波不稳定。

目前,已有许多文献对HVDC输电系统谐波进行了研究。文献[5]利用调制理论和开关函数研究了6脉动换流器直流侧电压和交流侧电流关系,并以此进行谐波分析,但此谐波分析方法需要测量初始电压电流值,存在一定的测量误差。文献[6-7]基于开关函数调制理论,分别利用阻抗频率特性和调制形成的关联矩阵特征值推导了谐波不稳定判据,但这些研究针对6脉动换流器进行,而实际工程中大部分都采用12脉动换流器,因此具有一定的局限性。文献[8]利用开关函数调制原理推导了交直流侧谐波交互参数矩阵并计算谐振衰减因子,提出了根据谐振衰减因子来判断12脉动换流器混合谐振型谐波不稳定的方法,但只考虑了整流器的作用。直流输电系统通常同时包含送端和受端,每个换流站的谐波相互作用不仅受其自身的影响,而且受其他换流站的影响[9],若简单地将整个逆变系统用理想电压源或电流源代替,必然会忽略其阻抗频率特性对整个系统谐波不稳定的影响。所以在分析谐波不稳定时必须考虑送、受端多桥换流器对系统谐波不稳定带来的影响。

本文基于开关函数调制理论,推导了同时考虑送、受端交流系统与直流系统间交互影响的单极12脉动换流器直流输电系统的谐波不稳定风险判据,该判据综合考虑了换流器换相过程的换相角、交直流侧等值谐波阻抗,以及换流变压器的铁芯饱和等因素。在电磁仿真平台PSCAD/EMTDC上搭建时域仿真模型并进行实例仿真分析,验证了本文所提判据的正确性。

1 直流两端对谐波不稳定影响的原理及等效模型

1.1 12脉动换流器开关函数调制理论

直流输电系统的谐波不稳定主要是由换流器对交/直流电压、电流非线性调制形成的正反馈引起的。由于换流器具有离散开关特性,可以用开关函数调制理论来简化交/直流电压、电流的关系[10-11],即交流电流由直流电流通过开关函数调制得到,直流电压由交流三相电压通过开关函数调制得到。

12脉动换流器由两个6脉动换流器串联而成,两个换流变压器的接线方式分别为Yy和Yd。12脉动换流器原理如图1所示。图中:Ia为换流变压器网侧a相电流;IaY和IaΔ分别为换流变压器Yy和Yd连接方式下的阀侧a相电流;Ua,Ub,Uc为换流变压器网侧a,b,c三相电压即交流母线电压;Id为换流器直流侧电流;UdY和UdΔ分别为上下两换流器对应的直流电压;Ud为直流侧极间电压。

图1 12脉动换流器原理示意图Fig.1 Schematic diagram of 12-pulse converter

由图1可知,换流桥在交流侧并联,在直流侧串联。考虑换相过程的12脉动换流器系统中,换流变压器网侧的交流电流幅值和直流侧的直流电压分别为:

(1)

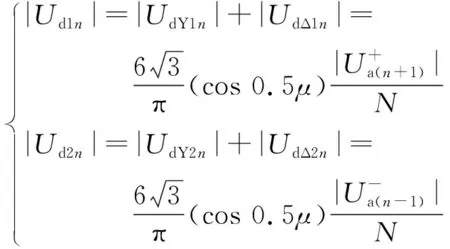
(2)

1.2 计及两端影响的谐波不稳定机理

通常HVDC输电系统的谐波不稳定包括频率互补谐振和换流变压器铁芯饱和型谐振,二者往往同时存在且共同作用[12-13]。交流侧并联谐振频率与直流侧串联谐振频率满足互补关系[14]时发生的谐波不稳定称为频率互补谐振。低次谐波分量通过换流变压器时,由于换流变压器发生偏磁产生较大相同频次的励磁涌流,使原有低频次谐波分量被放大,此谐波分量再通过换流器调制作用进一步放大,这样造成的谐波不稳定称为换流变压器铁芯饱和谐振。

换流变压器直流偏磁通常由交流系统故障引起,直流偏磁引起的励磁涌流中主要包含大量二次谐波分量[15]。铁芯饱和谐振主要表现为交直流系统低次谐波分量的交互影响,根据开关调制理论,假设直流系统存在一个很小的基频谐波电流分量,此直流基频谐波电流通过输电系统两侧换流器调制到交流侧,在两端交流系统产生正序二次谐波电流分量和直流电流分量。当形成的直流电流分量较大时,流过换流变压器直流侧绕组便会引起换流变压器铁芯饱和产生直流偏磁效应,在交流侧绕组上产生大量与直流电流呈线性关系的二次谐波电流[16],其与调制产生的二次谐波电流分量叠加作用于交流正序二次谐波阻抗,进一步产生交流二次谐波电压分量。两端的交流二次谐波电压分量通过整流器和逆变器同时调制回直流侧,产生基频谐波电压。二者电压共同作用于直流基频阻抗又形成直流基频谐波电流,从而形成了一个双向正反馈,如图2所示,这样的正反馈激励了谐波的放大。

图2 计及两端影响的铁芯饱和谐波回路Fig.2 Circuit diagram of core saturated harmonic considering effects of both ends

1.3 直流侧谐波阻抗等值电路

理想情况下,HVDC输电系统的换流器在交流侧等效为谐波电流源,在直流侧等效为谐波电压源。但由于交/直流系统间存在交互影响,且根据谐波不稳定形成机理,在分析考虑两端换流器影响的直流侧等值谐波阻抗模型时,必须考虑两端换流器阻抗对直流系统的影响。

对于12脉动换流器输电系统,从换流器直流侧向交流侧看进去,换流器与交流网络可等效为一个谐波电压源和一个谐波等值阻抗串联[11,17],则与图2相对应的直流侧等值谐波阻抗模型可简化为如图3所示。图中:Udr和Udi分别为换流器经过调制得到的整流侧和逆变侧直流电压;Zer和Zei分别为换流器等值到直流侧的整流侧和逆变侧谐波等值阻抗;Zs,Zf,Zl分别为平波电抗器、直流滤波器、直流线路等值阻抗。

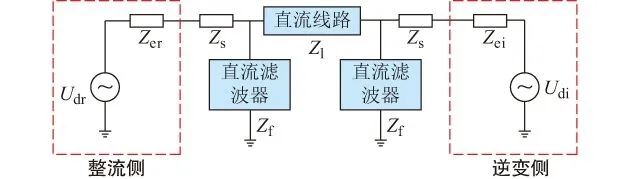
图3 直流侧谐波阻抗等值电路Fig.3 Equivalent circuit of harmonic impedance on DC side

考虑换流器换相角的影响,换流器直流侧等效阻抗会具有时变性。为简化计算,12脉动换流器直流侧谐波等值阻抗[18-19]表示为:

(3)

式中:Zcn为换流变压器n次等值阻抗,即换相阻抗。

2 谐波不稳定风险评估

2.1 仅考虑送端影响的谐波不稳定判据

文献[20]考虑换流变压器铁芯饱和引起的直流偏磁对谐波不稳定的影响作用,根据直流输电系统谐波不稳定机理,推导出只有送端系统的HVDC输电铁芯饱和谐波不稳定工程判据。文献[21]在文献[20]的基础上,考虑换流变压器叠加特性,进一步推导了多桥换流器HVDC输电送端的谐波不稳定判据,其中单极12脉动换流器的谐波不稳定判据为:

(4)

文献[20-21]在对所提工程判据进行仿真验证时,采用的验证模型均为文献[22]提出的只含整流器直流输电模型。但当整流侧和逆变侧同时存在时,无论系统哪一端交流侧或直流侧存在一个谐波源,且满足谐波不稳定发生条件时,此谐波源都将会在两端交/直流系统间形成交互作用,使系统发生谐波不稳定。在仅考虑送端影响的谐波不稳定判据基础上,进一步提出考虑两端换流器及交流系统影响的谐波不稳定评估方法,更准确地判断系统是否发生谐波不稳定。

2.2 计及两端影响的谐波不稳定判据

根据计及两端影响的谐波不稳定机理,仅考虑直流基频谐波分量与交流二次谐波分量。由式(1)所示电流调制关系(即n=2时),假设在t时刻直流系统存在一个基频谐波电流分量(为简化分析,设两端的初始电流幅值相同),设换流变压器铁芯饱和造成的直流偏磁效应所产生的二次谐波电流分量与直流基频谐波分量通过换流器调制到交流侧的直流谐波电流分量之比为k(k<1)[16],则考虑换流变压器铁芯饱和的整流侧和逆变侧两端换流变压器网侧二次谐波电流表示为:

(5)

当整流侧和逆变侧的交流二次谐波电流分别作用于各自交流系统二次谐波阻抗上时,产生的交流正序二次谐波电压为:

(6)

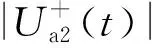
经过Δt时间后,两端交流电压又经换流器调制回直流侧,得到的直流基频电压为:

(7)

式中:|Ud11(t+Δt)|为(t+Δt)时刻交流正序二次谐波电压调制得到的直流基频谐波电压幅值,下标第1个1代表交流正序电压调制得到,第2个1代表基频。

直流侧等值电路如图3所示。从图中可以看出,直流系统电压由两端换流器调制而得的电压共同构成,则直流基频谐波电流为:

|Id1(t+Δt)|=

(8)

式中:|Id1(t+Δt)|为(t+Δt)时刻直流基频谐波电流幅值。

为判断整个输电系统是否会发生谐波不稳定,需要比较调制前后直流基频电流的幅值,令其比值为λ,即

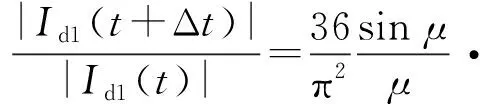
(9)

由式(9)可知,λ与换相角、两端交流二次谐波等值阻抗、直流基频等值阻抗、两端换流变压器变比、铁芯饱和程度有关,因此其中某个参数的不合理均容易导致系统发生谐波不稳定。当λ>1时,说明谐波电流被放大,系统存在发生谐波不稳定的风险;当λ<1时,说明谐波电流被吸收,系统不存在发生谐波不稳定的风险。

3 仿真验证与谐波不稳定分析

3.1 仿真模型及算例参数

为验证所提谐波不稳定判据的正确性,在只含整流器系统模型的基础上,加入逆变系统,建立如图4所示的单极12脉动HVDC输电系统模型。在正常运行时,整流器和逆变器的控制方式同CIGRE Benchmark模型。

图4 含两端换流器的HVDC输电系统模型Fig.4 Model of HVDC transmission system with two-terminal converters

根据前文所推导的判据,为了验证本文所提工程判据的正确性以及各因素对系统谐波不稳定是否会产生影响,选取多组网络参数进行对比分析。由于换流变压器的饱和程度与变压器的拐点电压有关,拐点电压越大,饱和程度越小,产生的谐波分量也较小。当拐点电压为1.25时,k在0.7左右;当拐点电压为1.35时,k在0.5左右;当拐点电压为1.05时,k在0.9左右[23]。各算例网络参数值设置如附录A表A1所示。

3.2 仿真及风险评估

根据前述的判据理论,总结其具体计算步骤如下。

步骤1:根据系统所提供参数值确定系数k,分别计算稳定情况下两端交流正序二次谐波等值阻抗、直流系统等值阻抗,以及换相角。

步骤2:再将步骤1中的参数以及换流变压器变比代入判据式(9)中,得到判据值λ。

步骤3:最后比较判据值λ与1的大小关系。若λ>1,说明系统存在发生谐波不稳定的风险;若λ<1,说明系统不存在发生谐波不稳定的风险。

为验证判据正确性,在仿真软件PSCAD/EMTDC上搭建如图4所示的仿真模型,依次对所有算例进行仿真。系统运行3 s时(此时系统已稳定运行),在整流侧交流母线上设置短路故障(为降低故障冲击电流过大,短路电阻为2 Ω),0.05 s后切除故障。

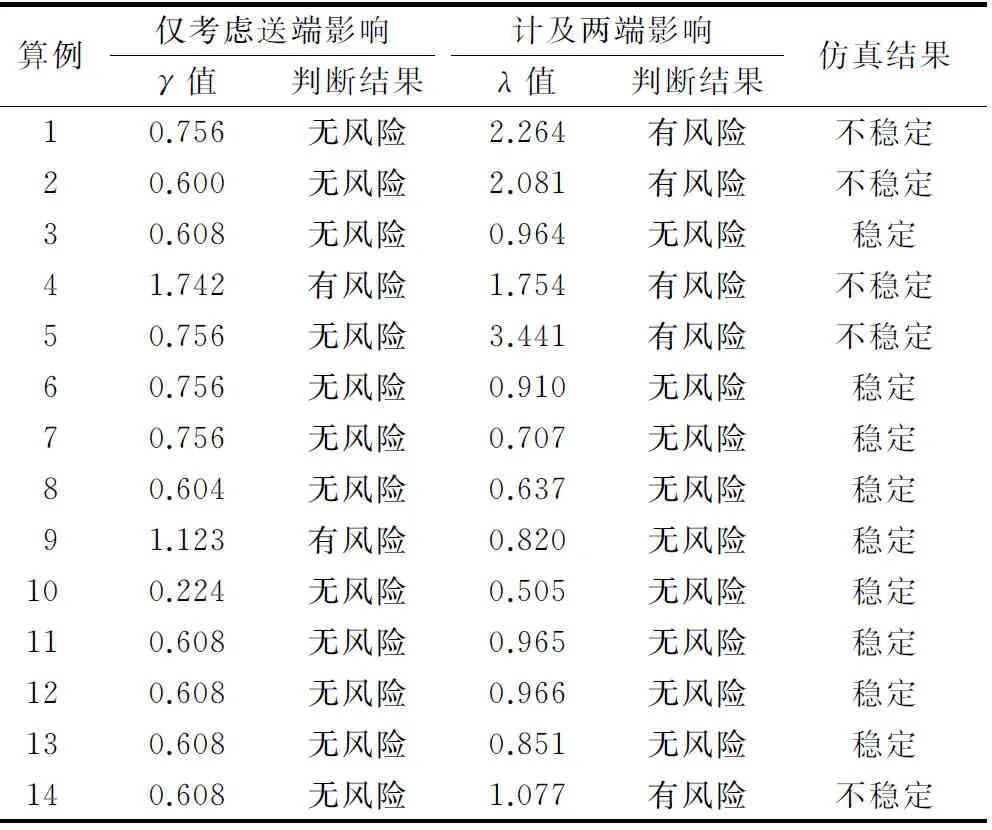
对各个算例采用文献[21]的判据和本文所提判据进行判断。按照判据计算步骤计算出各算例的γ值与λ值,并记录各算例的仿真结果。各算例判据值与仿真结果如表1所示。

根据谐波不稳定机理与判据理论分析,直流谐波分量经换流器调制至交流侧再调制回直流侧,因此通过直流谐波分量调制前后是否放大来判断系统是否发生谐波不稳定。其直流电流仿真波形如附录A图A1所示。

由表1中仿真结果以及附录A图A1的仿真波形可知,算例1,2,4,5,14中系统发生了谐波不稳定,其余算例均在故障切除后能很快恢复故障运行前水平,未发生谐波不稳定。从表1的结果可看出,仅考虑送端影响的谐波不稳定判据值γ在算例4,9中大于1,根据其理论判断这两个算例存在谐波不稳定风险,其余均不存在;而本文所提判据,算例1,2,4,5,14中的λ>1,其对应网络参数的系统工况存在发生谐波不稳定的风险,算例3和算例6至13中的λ<1,因此,可判断其对应网络的系统不存在发生谐波不稳定的风险。综合以上分析,判断有两端交流系统存在的HVDC输电系统是否存在谐波不稳定风险时,仅考虑送端影响的谐波不稳定判据,在1,2,5,9,14等5个算例中,判据的计算结果与仿真结果不一致;本文所提考虑送端与受端共同影响的谐波不稳定判据计算结果与仿真结果一致。

综上所述,在实际存在两端交流系统时,仅考虑送端影响的谐波不稳定判据具有一定的准确性,但当两侧交流系统谐波阻抗、直流系统谐波阻抗、铁芯饱和程度等任一参数改变时,此判据均存在判断不准确的情况。本文在其基础上提出的工程判据更具有准确性与实用性。

3.3 影响因素分析

针对图4所示系统进行谐波不稳定影响因素分析。

1)送端交流系统参数的影响。算例1至4为受端交流系统参数和直流系统参数分别相同,以0.5 mH为步长改变送端的电感值,对比算例1和3可知,送端系统阻抗值对系统谐波不稳定有影响,且可以看出此系统在送端交流系统电感值高于或低于6.27 mH时,系统表现为谐波不稳定。

2)受端交流系统参数的影响。算例1和算例5至7为送端交流系统参数和直流系统分别相同,改变受端两个电感的数值,对比算例1和6可知,受端系统阻抗值对系统谐波不稳定有影响,且可以看出此系统在受端交流系统电感值低于36.5 mH时,系统表现为谐波稳定。

3)直流系统参数的影响。算例7至9为送端与受端交流系统参数分别相同,以2 μF为步长改变直流系统的电容值,可以看出此系统当直流系统电容值在24～28 μF范围内时,系统表现为稳定。算例1和10为送端与受端交流系统参数分别相同,改变直流系统的电感值,可以看出直流系统阻抗值对系统谐波不稳定有影响,且此系统当直流系统电感值更小时表现为稳定。

4)换相角的影响。算例3,11,12为系统换相角不同,其余参数均相同,由附录A图A1可以看出换相角更接近30°时,系统在故障后能更快恢复到运行前水平。对比算例3和12,从仿真结果及以上分析可以看出,虽然两算例都未发生谐波不稳定,但算例3相较于算例12能更快恢复稳定状态,说明换相角的变化会影响系统谐波不稳定性。

5)换流变压器饱和程度的影响。算例3,13,14为换流变压器饱和程度不同,其余参数均相同。对比算例3和14可知,当铁芯饱和达到一定程度时,原本稳定的系统会发生谐波不稳定,则铁芯饱和程度的改变会影响系统的谐波不稳定,且可以看出饱和程度越大,越容易发生谐波不稳定。

因此,在实际应用中能够利用此判据初步选定系统参数,并且判断系统是否存在谐波不稳定风险。

从附录A图A1(a),(b),(d),(e),(n)可以看出,算例1,2,4,5,14在故障切除后,直流电流一直维持故障后的大幅度振荡状态,并不能在短时间内使系统恢复稳定,说明此系统在这5个算例的网络参数下发生了谐波不稳定。同时,对直流电流和交流电流进行快速傅里叶分解后,直流基频分量与交流二次谐波分量最大,说明发生了铁芯饱和谐波不稳定。从附录A图A1(c),(f)至(m)可以看出,系统在故障切除后只有一点轻微的振荡,并在1 s内快速恢复至故障前运行水平,说明在相应算例下,此系统未发生谐波不稳定。比较9个未发生谐波不稳定的仿真波形图,其中附录A图A1(j)恢复时间最短,波动水平也较小。综上所述,本系统可以选取算例10的网络参数,能保证在系统发生故障并切除后更快趋于稳定,减小谐波不稳定发生的风险。

4 结语

实际的HVDC输电系统包括整流站、直流线路、逆变站3部分,且多为12脉动换流桥,因此由于有多个换流器的存在,使整个系统成为了多谐波源系统。系统中的所有谐波通过换流器在交直流系统之间的调制相互影响。在理论分析其谐波不稳定是否发生时,要考虑3部分之间的相互影响作用。

本文建立包括3部分的直流输电系统模型,利用换流器开关调制理论推导考虑3部分阻抗—频率特性关系的单极12脉动换流器HVDC输电系统的谐波不稳定风险评估判据。根据风险评估值λ是否大于1来判断:若λ>1,系统存在发生谐波不稳定的风险;若λ<1,系统不存在发生谐波不稳定的风险。通过理论计算和电磁暂态仿真对比验证了本文判据能准确判断系统是否存在发生谐波不稳定的风险,且验证了谐波不稳定的影响因素,能通过判据计算确定系统参数选取,具有一定的实际意义和参考价值。

本文提出的谐波不稳定判据还可推广到其他更复杂的多桥换流器输电系统中。但本文所提判据由于只考虑了交流二次谐波阻抗和直流基频阻抗幅值间的关系,存在一定的误差,因此在后续研究中需要再研究其他各次谐波阻抗以及阻抗矢量性的影响。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。