考虑新型拓扑结构的统一潮流控制器五端功率注入模型

吴 熙, 殷天然, 祁万春, 蔡 晖, 蒋 平, 陈 琛

(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 国网江苏省电力有限公司电力经济技术研究院, 江苏省南京市 210096)

0 引言

统一潮流控制器(unified power flow controller,UPFC)被认为是第三代柔性交流输电系统(FACTS)器件中最具代表性、功能最强大的控制器,近些年得到了广泛的关注。UPFC具有多种控制模式,可以对输电线路电压、相角、阻抗和母线电压进行调节控制,可以灵活快速地对输电线路中的潮流进行调控,为电网潮流控制提供了一个新的手段[1-3]。

目前UPFC的理论研究比较丰富,但真正投运的UPFC工程较少。国外仅有三个工程实现投运,包括1998年美国Inez工程[4-5]、2001年美国Marcy工程[6]、2003年韩国Kangjin工程[7],限于当时的技术水平,工程尚处于积累运行经验阶段,在投运后一直未有新的工程投运。2015年底,南京西环网统一潮流控制器示范工程(简称“南京UPFC工程”)作为国内首个、世界第四个UPFC工程成功投运,用于解决南京西环网长期存在的潮流分布不均、供电能力不足问题[8]。2017年,苏州南部电网UPFC示范工程正式投运,以增强江苏电网可控能力[9]。南京UPFC工程中,UPFC装置串联侧通过两个换流器控制220 kV铁北—晓庄双回线路,并联侧连接在燕子矶35 kV低压母线上,构成了串联侧控制双回线路,并联侧连接低压母线的新型拓扑结构[8-11]。该结构具有如下优势:①双回线功率独立控制,双线N-1后仍可发挥一定控制作用,可靠性增强;②减小并联变压器的成本和体积,降低变压器绝缘等级,提高35 kV系统的无功储备能力[8]。一方面,国内大部分110 kV及以上电网多采用双回线路结构;另一方面,大部分国内220 kV城市电网和南京西环网一样为交流强电网,交流电压较为稳定,系统对无功补偿需求不大,故对UPFC并联侧进行经济性的优化,将并联侧换流器接入点由原母线改接至其他需要无功补偿或调节电压的母线[10]。因此,综合其经济性、可靠性和灵活性多方面的优势,该UPFC新型拓扑结构具有广泛的应用前景[11]。

随着电网规模和负荷水平的发展,UPFC在解决大电网潮流问题极具竞争力,开展UPFC的系统级分析具有重要意义。国内外对UPFC的系统级仿真建模已展开大量研究[12-19]。其中,功率注入模型是基于功率注入法将UPFC对系统的影响等效到对应线路的两侧节点上,在不修改潮流计算中原本节点导纳阵的情况下,嵌入UPFC模型,最大限度利用传统潮流计算中雅可比矩阵形成的公式和经验[13]。因而功率注入模型在大电网潮流计算中得到了广泛应用。文献[13-14]在PSASP中建立了UPFC两端注入模型,但实际工程中,考虑经济性问题,往往会将UPFC的并联侧接入电压等级更低的母线上,典型模型无法适应于这种新型的拓扑结构。文献[18-19]对上述情况进行了考虑,文献[18]研究了UPFC并联侧与串联侧接于不同母线情况下的潮流计算方法。文献[19]提出了一种UPFC三端功率注入模型,计及了UPFC并联侧节点接入低压母线带来的影响,但该文只考虑了UPFC串联侧接单回线路,虽然可将双回线等效为单回进行潮流计算,但无法进行该双回线的N-1校核,UPFC所在双回线N-1后控制特性也无法模拟。然而,国内220 kV等级及以上电网大量采用双回线以提高电网可靠性,相应的,UPFC串联侧接双回线的拓扑结构有很强的使用价值。现有的UPFC功率注入模型无法实现串联双回线N-1校核,切实反映工程结构的UPFC建模研究和系统级分析还有待补充。

本文提出了一种反映实际工程拓扑结构的UPFC五端功率注入模型,该模型不仅实现了UPFC串联侧控制两回线路的功能,还考虑了UPFC并联侧的灵活连接性。利用功率注入法推导了该模型的数学表达式,基于PSASP软件的用户自定义(UD)功能搭建该模型,阐述含UPFC潮流计算的实现原理和该模型的串联双线控制策略。采用该模型进行大电网仿真计算,该模型在系统正常状态及UPFC串联双线N-1故障时实现了双线控制策略,保障系统安全稳定运行。

1 UPFC五端功率注入模型

1.1 南京工程中的UPFC结构及工作原理

南京西环网供电的主要输电通道存在较严重的潮流分布不均情况,尤其是西环网内220 kV晓庄南送断面潮流过重情况尤为突出,影响了西环网的整体功能能力和安全可靠水平,工程通过安装UPFC解决西环网存在的潮流不均问题[10]。南京UPFC工程的UPFC新型拓扑结构如附录A图A1所示[11]。该UPFC包括2个串联侧换流器和1个并联侧换流器,3个换流器采用背靠背的连接方式,通过隔离开关连接[8]。

1)串联换流器接入方案:串联换流器经两个串联侧变压器,分别串入220 kV铁北—晓庄双回线路,通过对铁北—晓庄线路的潮流控制实现对晓庄南送断面的潮流控制[8-9]。

2)并联换流器接入方案:由于在UPFC安装区域无功补偿的需求不大,并联侧主要用于补偿串联侧与线路交换的有功功率,因此并联侧换流器经变压器接入站内燕子矶35 kV母线。一方面,并联变压器的成本和体积减小,变压器绝缘等级降低;另一方面35 kV系统的无功储备能力得到提高[11]。

其工作原理如下。

2)并联侧控制:并联侧换流器能够独立向系统交换无功功率,通过与系统交换无功功率可控制并联侧接入点的节点电压。同时,并联侧换流器需提供或吸收串联侧换流器与系统交换的有功功率,维持UPFC的有功平衡。

1.2 UPFC五端功率注入模型的数学推导

UPFC串联侧理想电压源和电抗合成得到对应的等效电压源为:

(1)

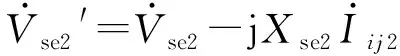
(2)

并联侧电压源和并联侧输出电流的关系为:

(3)

将UPFC对系统的影响等效为UPFC对5个节点i1,i2,j1,j2和k的附加注入功率Si1s,Si2s,Sj1s,Sj2s和Sks,建立UPFC五端功率注入模型如图1所示。

图1 UPFC五端功率注入模型Fig.1 Five-terminal power injection model of UPFC

图1中,Sij10和Sij20分别表示不含UPFC时线路i1-j1和i2-j2上的自然潮流,表达式如下:

Sij10=Sij20=

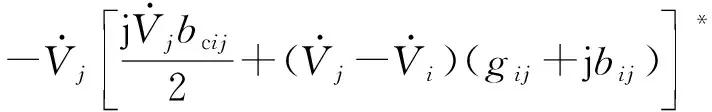
(4)

式中:*表示共轭。

推导五端功率注入模型中各注入功率的表达式。以节点j1为例,UPFC在节点j1的附加注入功率Sj1s可由加入UPFC后的传输功率与未加UPFC时的自然功率相减得到,即Sj1s=Sij1-Sij10。

加入UPFC后的传输功率Sij1为:

(5)

计算得到节点j1和节点j2的有功注入和无功注入表达式如式(6)至式(9)所示。

Pj1s=VjVse1′(gijcos(θse1′-θj)-bijsin(θse1′-θj))

(6)

Qj1s=-VjVse1′(gijsin(θse1′-θj)+

bijcos(θse1′-θj))

(7)

Pj2s=VjVse2′(gijcos(θse2′-θj)-bijsin(θse2′-θj))

(8)

Qj2s=-VjVse2′(gijsin(θse2′-θj)+

bijcos(θse2′-θj))

(9)

同理,可以推出节点i1,i2的注入功率,见式(10)至式(13)。

Pi1s=-ViVse1′gijcos(θse1′-θi)-

(10)

Qi1s=ViVse1′gijsin(θse1′-θi)+

(11)

Pi2s=-ViVse2′gijcos(θse2′-θi)-

(12)

Qi2s=ViVse2′gijsin(θse2′-θi)+

(13)

根据UPFC自身有功平衡,即UPFC串联侧产生的有功和并联侧吸收的有功应相等[1],有

Psh+(Pse1+Pse2)=0

(14)

式中:Psh为UPFC并联侧注入有功功率;Pse1和Pse2分别为各串联侧向线路注入有功功率。

(15)

由式(15)得到节点k的有功注入表达式为:

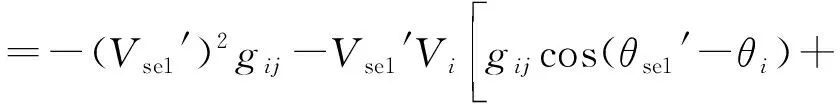
(16)

节点k的无功注入表达式为:

Qks=VkIq

(17)

式(6)至式(13)、式(16)和式(17)分别表示节点i1,i2,j1,j2,k的注入有功和无功功率,从而构成了UPFC五端功率注入模型。

根据规划,UPFC装置成套投运时,UPFC受其换流器容量限制[8],相同电压等级的普通变压器,串联变压器的额定电压低,容量小[20]。串联侧容量计算如式(18)所示。

(18)

式中:Vse1,max和Vse2,max为串联变压器最大电压值;Iij1,max和Iij2,max为串联线路最大电流值。

并联侧容量主要受串并联侧交换的容量限制,需要保证与串联侧的换流器有功交换能力即可[8]。

2 含UPFC五端功率注入模型的系统级分析

2.1 基于PSASP/UD的潮流计算原理

PSASP软件开发了UD功能,通过UD模型的输入信息和输出信息与电网实现连接。PSASP/UD的实现方式为:潮流计算时,UD从PSASP潮流程序(LF)的数据接口中读取输入信息,计算完成后再将输出信息从数据接口返回给LF程序,实现LF与UD的交替求解,直至计算达到控制目标值[19]。基于PSASP/UD搭建UPFC五端功率注入模型,可实现含UPFC的系统潮流计算,从而分析UPFC的潮流控制能力。

UPFC五端模型的输入信息分别为:节点i1,i2,j1,j2,k的电压幅值和相角,受控线路潮流Pij1,Qij1,Pij2,Qij2;UPFC的输出信息为节点i1,i2,j1,j2,k的注入有功和无功功率;UPFC控制目标共有5个,为受控线路潮流Pref1,Qref1,Pref2,Qref2和受控节点电压Vref。

因此,潮流计算的收敛条件应为:

(19)

加入UPFC之后,线路i1-j1和i2-j2上的潮流Pij1,Qij1,Pij2,Qij2与未加UPFC的自然潮流Pij10,Qij10,Pij20,Qij20以及节点j1和j2的注入功率Pj1s,Qj1s,Pj2s,Qj2s之间存在如下关系:

(20)

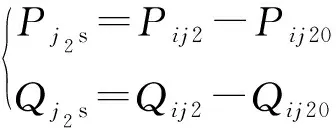
(21)

将串联侧两回线路潮流目标值Pref1,Qref1,Pref2,Qref2,分别替换式(20)和式(21)中的Pij1,Qij1,Pij2,Qij2,已知自然潮流的情况下即可得到节点j1和j2侧的注入功率Pj1s,Pj2s,Qj1s,Qj2s。

对于节点k,其注入的有功功率Pks可根据功率平衡直接得到,但注入无功功率Qks中含有未知参数Iq。由于UPFC并联侧采取节点电压控制方式,即节点k电压幅值恒定,节点k为PV节点,Qks不需要参与迭代[13],待潮流收敛后根据Qks即可求出Iq。

基于功率注入模型采用牛顿—拉夫逊法进行潮流计算,无需修改雅可比矩阵结构,仅需增加UPFC对相关节点产生的附加注入功率值,修正节点i1,i2,j1,j2,k的功率,即可进行迭代计算。

(22)

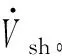
综上,基于PSASP/UD,含五端功率注入模型的潮流计算的具体步骤如下。

步骤1:LF程序启动,进行初始潮流计算,得到线路的自然潮流和各节点初始的电压幅值和相角,即UPFC的输入信息。

步骤2:UD从接口读取UPFC的输入信息,根据设置的UPFC控制目标,由式(20)、式(21)和式(22)可以计算得到UPFC的控制参数Vse1′,θse1′,Vse2′,θse2′。

步骤3:根据Vse1′,θse1′,Vse2′,θse2′,由式(6)至式(13)和式(15)可得到各节点注入功率Pi1s,Pi2s,Qi1s,Qi2s,Pj1s,Pj2s,Qj1s,Qj2s,Pks,即UPFC的输出信息。

步骤4:LF程序获得UD的输出信息,修正对应节点功率,重新进行潮流计算,得到新的输入信息。

步骤5:UD获取新的输入信息,判断是否满足收敛条件(式(19)),若不收敛,回到步骤2;若收敛,可计算得到最终的UPFC串联侧控制参数和并联侧控制变量。

2.2 UPFC五端功率注入模型的控制策略

基于文中所建立的UPFC五端功率注入模型,可进一步开发UPFC的装置级和系统级控制策略,以模拟UPFC的动态控制特性。

本文采用的装置级控制策略为:串联侧为双回线路功率控制模式,控制双回线路的有功和无功功率为指定值;并联侧为节点电压控制模式,控制并联节点电压为指定值,具体建模方法参照文献[21],在此不再赘述。

为保障UPFC在其串联侧线路正常运行和N-1故障时均能有效控制,建立UPFC五端模型的系统级控制策略如图2所示。图中:Pset,N为双回线路的正常功率限额;Pset,F为N-1故障下的事故功率限额;Pmax和Pmin分别为线路的最大传输功率和最小传输功率;Pref为UPFC的控制目标设定值。

图2 UPFC五端模型的双线控制策略Fig.2 Double-line control strategy of UPFC five-terminal model

由图2可知,UPFC五端模型的双线控制策略为:①在系统正常运行状态下,双回线路按照各自的功率目标值进行控制;②当双线发生N-1故障时,故障线路对应的换流器停运,UPFC设置故障后线路功率目标值,对剩下一回线进行控制,使其满足N-1校核。

3 仿真实例

本文在PSASP中基于南京西环网系统采用2015年冬季运行方式数据进行仿真,将搭建的UPFC五端模型加入该系统UPFC接入南京西环网的接线图见附录A图A3[22]。南京西环网中,铁北—晓庄双线两端节点和35 kV燕子矶节点对应UPFC五端功率注入模型的5个节点i1,i2,j1,j2,k,UPFC的控制目标为受控线路潮流Pref1,Qref1,Pref2,Qref2和受控节点电压Vref。

未安装UPFC时,系统初始潮流计算得到铁北—晓庄每回线路功率各为1.94-j0.20(标幺值),燕子矶35 kV母线电压为0.999 8(标幺值)。加入UPFC后,设置UPFC参数:串联侧变压器最大输出电压为Vse1,max=Vse2,max=0.115(标幺值),内电抗Xse1=Xse2=0.003 7(标幺值),并联侧变压器内电抗Xsh=0.004(标幺值),并联侧输出电流最大值Ish,max=2.0(标幺值)。设置目标值的控制精度为0.001。工程应用中UPFC主要用于控制断面有功功率,解决断面过载问题[23]。在系统正常运行情况下,采用本文UPFC五端功率注入模型可以准确控制线路潮流和节点电压,使误差在精度范围内,并解决南京西环网内断面过载问题。该模型稳态控制的详细验证见附录B,本文主要介绍该模型动态控制效果。

3.1 UPFC串联侧N-1故障仿真

根据2.2节的UPFC五端模型的双线控制策略,双回线N-1故障下,故障线路的UPFC换流器停运,串联侧仅保留一台换流器对剩下一回线路进行控制。设图1中线路i1-j1断路,仅剩线路i2-j2,五端模型故障后的控制目标剩下3个,为Pref′,Qref′和Vref′。令线路故障后仍维持正常状态的传输水平(可根据实际需求设置其他数值),则故障前后目标值的关系如下:Pref′=Pref2,Qref′=Qref2,Vref′=Vref。

故障前,设置燕子矶35 kV节点电压目标值为1.00(标幺值),铁北—晓庄每回线路有功和无功目标值分别为1.6(标幺值)和-0.2(标幺值)。t=2 s时,铁北—晓庄线路发生N-1故障,采用UPFC五端模型依据双线控制策略进行N-1故障控制,仿真时间为10 s,仿真结果如图3所示。

图3 UPFC串联侧N-1故障仿真结果Fig.3 Simulation results under N-1 contingency of UPFC series side

由图3可知,UPFC串联侧N-1故障发生后能根据设定的控制目标值对受控线路潮流进行有效的控制,使系统迅速稳定在故障目标值,仿真结果验证了UPFC在串联侧N-1故障发生下该模型的动态控制能力,体现了本文提出的五端模型的双线控制能力。

3.2 与已有模型对比仿真

为了进一步分析该模型的必要性,采用已有的UPFC三端功率注入模型[19]与本文提出模型进行对比。UPFC三端功率注入模型与本文提出模型的区别在于,三端模型将铁北—晓庄双线等效成一回线路,线路阻抗为两回线的等效阻抗gij,bij和bcij,将UPFC的两个串联侧电压源等效为一个串联侧电压源Vse,UPFC的影响等效为三个节点i,j,k的注入功率Sis,Sjs和Sks,见附录A图A4。

相较于五端模型,三端模型的控制目标共有三个Pref,Qref,Vref。其中Pref和Qref表示铁北—晓庄两回线路的有功和无功功率总和,Vref表示35 kV燕子矶节点电压。设置UPFC参数:等效内电抗Xse=0.001 85(标幺值),为两个串联变压器的内电抗之和,其他参数与五端模型一致。

为使仿真对比具有实际意义,采用两种模型在南京电网进行仿真,令两种模型中的受控线路铁北—晓庄两回线路功率总和相同,节点电压目标值相同,使UPFC在稳态时对系统的控制效果完全相同,比较两种模型在故障前后的控制效果。为便于对比,两种模型的输出功率设置为铁北—晓庄双线功率之和。设置节点电压目标值为1.00,受控双回线路的有功和无功功率分别为2.00和-0.40。t=2 s,受控线路发生N-1故障,仅剩一回线路对应的有功和无功目标值变为1.00和-0.20。仿真时间为10 s,得到仿真结果如图4所示,具体数值可见附录C表C1。

由图4(a)和(b)可知,当UPFC串联侧发生N-1故障时, UPFC三端模型和UPFC五端模型均能在故障前后能根据设定的控制目标使受控线路有功和无功功率稳定在目标值。

由图4(c)可以看出,两种模型的串联侧控制参数Vse在故障前相等,但故障后存在较大差异。这是由于UPFC三端模型的串联侧电压源内电抗为两个电压源合并后的等效阻抗,然而当故障发生后实际应仅剩一个电压源内电抗,但三端模型对应的电抗数值无法更改,因此三端模型在故障后得到的控制参数Vse′是错误的。在该算例中,故障后三端模型对应参数Vse′已达到其极限值0.115,此时UPFC只能按照参数最大值进行控制,故障后受控线路有功功率为1.051 4,无法达到其目标值1.00,误差为5.14%,无法体现实际工程中UPFC真实的控制效果。本文提出的五端模型可以准确得到实际拓扑结构的UPFC控制参数,且能够实现受控线路有功功率的准确控制。

图4 采用两种模型的N-1故障仿真结果Fig.4 Simulation results when adopting two models under N-1 contingency

当受控双回线路的有功功率设置为3.20时,具体仿真结果可见附录C。此时,故障后三端模型的串联侧控制参数Vse′=0.104 1,五端模型的控制参数Vse′=0.070 3,误差达到48.08%。

在工程规划中,串联变压器是UPFC成套装置中最重要的设备之一,串联变压器能够保障线路长期稳定运行[24],容量按式(18)计算。在本文系统仿真中,若采用三端模型评估UPFC的控制能力,由于Vse′存在的较大差异,会严重影响UPFC的容量估计。而本文提出的模型在双线N-1故障下可以获取较为精确的UPFC控制参数值,更符合工程实际需求。

4 结语

本文针对实际工程采用功率注入法提出了一种UPFC五端功率注入模型,实现了含UPFC五端模型的潮流计算,并建立了UPFC串联侧分开控制双回线路的控制策略。以南京西环网UPFC工程为例采用本文模型实现仿真,并与已有模型进行了比较,UPFC五端功率注入模型不仅实现了UPFC串联侧独立控制两回线路的功能,且考虑了UPFC并联侧换流器的灵活连接性,能够准确反映N-1故障下UPFC的控制效果,可以为实际工程UPFC运行和控制策略研究提供技术支撑。本文在进行动态分析时,仅考虑了定功率控制策略,下一步可以基于该五端功率注入基础模型,开发定电压、定阻抗和定相角控制策略仿真包,以实现对UPFC各种控制策略的特性评估。

本文受到国网江苏省电力有限公司科技项目“500千伏UPFC接入苏州南部电网控制策略深化应用研究”(J2017053)的资助，特此感谢！

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。