三相VIENNA整流器双闭环控制策略及其参数研究

汪 鹏 ，李 山 ，郭 强 ，陈 敏 ，宋立风 ，李 晓

（1.重庆理工大学电气与电子工程学院，重庆 400054；2.重庆市能源互联网工程技术研究中心，重庆 400054）

目前，对三相PWM整流器研究日趋成熟，其广泛应用于静止无功发生器SVG（static VAR generator）、有源电力滤波 APF（active power filter）、高压直流 HVDC（high voltage direct current）输电、新型不间断电源 UPS（uninterruptible power supply）中[1]。但随着应用领域的扩展以及功率等级和电压等级的升高，传统两电平PWM整流器很难在中大功率场合获得理想的效果。研究表明多电平PWM整流器相比于两电平能使网侧电流谐波和装置损耗更小，提高装置效率，并且在中大功率场合能获得更好的应用效果[2-4]。

在三电平整流器拓扑中，奥地利维也纳大学Kolar教授于1994年提出的VIENNA整流器[5]，具有开关器件少，开关管应力小，无需考虑上下开关管死区等优点，得到越来越多的科研人员关注，并开展了广泛研究[6]。目前，针对VIENNA整流器的控制策略，国内外学者进行了大量研究[7-11]。研究表明对VIENNA整流器的控制主要实现网侧电流快速跟踪电网电压、稳定直流母线电压、单位功率因数运行、直流侧中点电位平衡等要求[12-13]。其中，文献[14]采用了单周期控制技术，提出在调制方案中注入3次谐波电流的控制策略，从而提高了直流电压利用率。但存在3次谐波电流获取较为困难的缺点；文献[15]采用了滞环电流控制技术，将中点电位偏差引入滞环电流闭环控制中，实现对直流侧中点电位的平衡控制。具有硬件设备简单、电流偏差小的优点，但存在开关频率随电流变化波动、滤波电感设计困难等缺点；文献[16-18]重点分析了VIENNA整流器的SVPWM调制技术，提出三电平向两电平等效转换的方法，简化了传统三电平调制中复杂的三角运算，同时在调制中运用正负小矢量抵消来平衡中点电位偏差；文献[19]给出了一种新型ABC自然坐标系下，电网三相不平衡时的VIENNA整流器控制方法，大大简化了传统双坐标变换法的控制复杂程度。

针对以上问题，为实现对VIENNA整流器简单、高效、可靠的控制，本文设计了针对VIENNA整流器的双闭环控制策略，并以控制器参数设计为研究重点。首先分析了该型VIENNA整流器的工作原理并建立其在d-q坐标系下的数学模型；其次，在其数学模型基础上设计了电压外环和电流内环的双闭环控制策略，利用MTALAB/SISO设计工具着重分析了电压外环和电流内环控制器参数对控制对象的影响，并从中选取最优参数。相比于传统PI控制器设计，此种方法具有控制结构简单，计算量小和动态响应快等优点；最后利用MTALAB/SIMULINK软件搭建仿真模型验证控制策略及其参数设计的正确性和可行性。

1 VIENNA整流器工作原理及数学建模

1.1 VIENNA整流器工作原理

三相VIENNA整流器主拓扑如图1所示。其中ea、eb、ec为三相输入电源，L 三相输入滤波电感，C1、C2为直流侧滤波电容，Si（i=1,2,…,6）分别为各相桥臂上下开关管，DW+与DW-二极管与组成双向开关管。DF+与DF-为每相桥臂上下的快恢复二极管。当三相输入电压平衡，以及直流侧上下电容电压对称时，忽略开关管中的高频谐波分量，此时直流侧中点O与输入三相电源的中点N等效。以A相为例，对电感电流在连续导电模式CCM（continuous conduction mode）下电路模态进行分析。

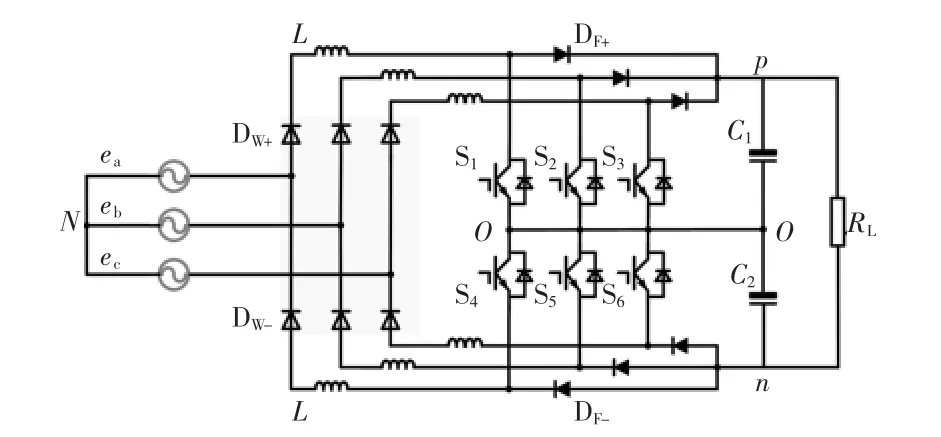
图1 三相VIENNA整流器主拓扑Fig.1 Main topology of three-phase VIENNA rectifier

当S1断开时，A相电流通路为 N→DW+→L→DF+→O→n，此过程交流侧电感电压 UL=ea－0.5Udc＜0，电感电流iL>0，且逐渐减小，负载由电源、电容C2和电感L提供能量，同时电源和电感L向电容C1充电储能。整流器交流侧电压UAO=0.5Udc，如图2（b）所示。

当电源电压工作在负半轴时，即ea＜0时，由于二极管DW+的反向阻断作用，开关管S1导通与否不参与对A相电流的控制，A相电流的控制只与开关管S4有关。当S4导通时，A相电流的通路为n→O→S4→L→DW－→N，此过程交流侧电感 UL=ea＜0，电感电流iL＜0，且逐渐增大，并处于反向储能阶段，负载由直流侧电容C1和C2提供能量。整流器交流侧电压 UAO=0，如图 3（a）所示。

当S4断开时，A相电流的通路变为N→O→DF→L→DW－→N，此过程交流侧电感电压 UL=ea+0.5Udc>0,电感电流iL＜0，且逐渐减小，负载由电源、电容C1和电感提供能量，同时电源和电感L向电容C2充电储能，整流器交流侧电压UAO=－0.5Udc，如图 3（b）所示。

由于二极管DW+和DW－的作用使得每相桥臂的上下开关管不能直通，从而在开关管的控制信号上无需设置死区，另一方面，也阻碍了能量的双向流动，使得该型整流器仅具备单向整流功能。同时相比于传统三相三开关VIENNA整流器，该型VIENNA整流器工作时，任意时刻每相桥臂只有一个开关管参与对电流控制，这一特性有助于另一开关管和电感散热，提高整流器整体可靠性。

模型右边的M(θ)为5×5惯性力矩阵，它是由机械手自身运动所产生的；为5×1矩阵，它是离心力和科氏力；G(θ)表示机械手自身重力。要考虑到系统运动时平台和机械手之间的相互作用力对模型的影响，那么等式的右边应该还包括由平台的运动在机械手上产生的惯性力离心力和科氏力表示移动平台的速度。这些力和力矩可以由平台部分的结构参数和机械手的动力学方程计算得到，即机械手的逆动力学模型为：

1.2 VIENNA整流器数学建模

在对上述工作原理的分析基础上，建立VIENNA整流器等效开关模型，如图4所示。ek为电网电压，L为滤波电感，R为滤波电感等效电阻，ik为交流侧输入电流，udc1和udc2为直流侧电容C1和C2上的电压，RL为负载等效电阻。Sk为各相开关电位状态，各开关电位规定为

图2 电源电压大于零时，整流器工作原理Fig.2 Operation principle of rectifier under the condition of ea＞0

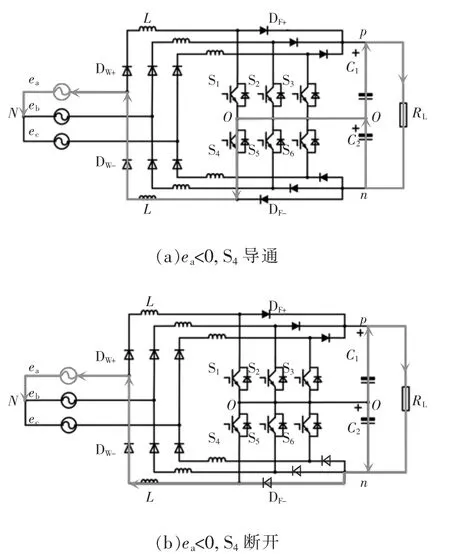
图3 电源电压小于零时，整流器工作原理Fig.3 Operation principle of rectifier under the condition of ea＜0

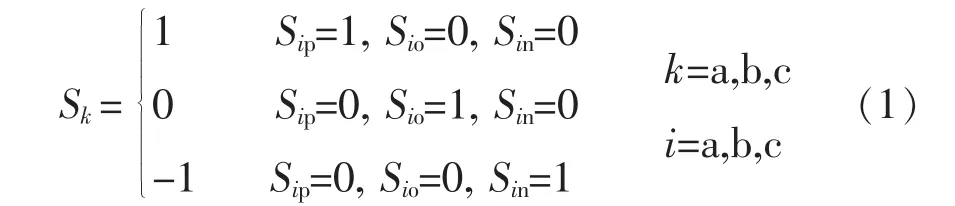
当电网电压三相平衡仅含基波分量时，得到VIENNA整流器在d-q坐标系下的数学模型

式中，ed、eq和id、iq分别为两相旋转坐标系下的电网电压和电流。由式（2）得其等效电路模型如图5所示。

图4 VIENNA整流器等效开关模型Fig.4 Equivalent switch model of VIENNA rectifier

图5 d-q坐标系下等效电路Fig.5 Equivalent circuit in d-q reference frame

由图5不难看出，系统模型中存在耦合项ωLid和ωLiq，使得在d-q坐标系下系统仍具有非线性、强耦合的特点。因此，在对控制策略设计时应尽量消除耦合项的影响。

2 VIENNA整流器双闭环控制策略

在VIENNA整流器d-q坐标系建模的基础上，选取d轴为有功功率参考轴，q轴为无功功率参考轴，从而实现对VIENNA整流器有功、无功分量的独立控制。在对三相VIENNA整流器控制系统设计时，采用电流内环和电压外环的双闭环控制，电流内环主要作用是按电压外环输出的电流指令进行电流控制，实现单位功率因数正弦波电流控制，电压外环主要是控制整流器直流侧电压的稳定。VIENNA整流器双闭环控制框图如图6所示。

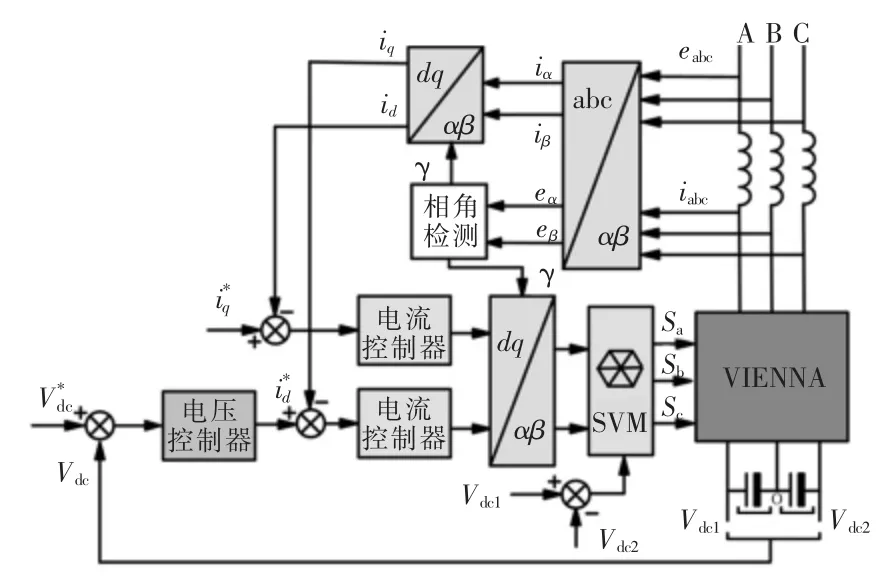
图6 VIENNA整流器双闭环控制框图Fig.6 Block diagram of dual closed-loop control of VIENNA rectifier

2.1 电流内环控制系统设计

为消除耦合项ωLid和ωLiq影响。在电流内环设计时，采取前馈解耦控制策略，实现对d、q轴的独立控制。VIENNA整流器电流内环控制框图如图7所示，图中，i*d和i*q分别为d、q轴指令电流，为实现单位功率因数控制，通常令i*q=0，其中Gi（s）为电流内环控制器传递函数。

通过引入前馈解耦控制策略，三相VIENNA整流器d轴电流控制框图如图8所示，可得电流内环的开环传递函数为

图7 VIENNA整流器电流内环控制框图Fig.7 Block diagram of inner current loop control of VIENNA rectifier

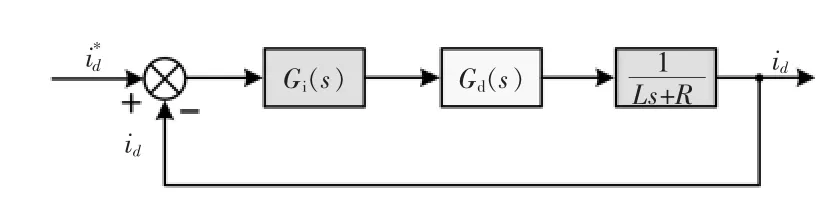
图8 电流内环控制框图Fig.8 Block diagram of inner current loop control

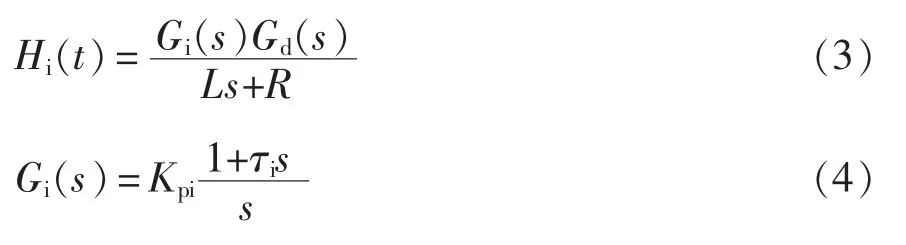
式中，Gd（s）为电流内环采样延迟与输出延迟的等效传递函数，用1阶惯性环节近似等效为

式中，Td≈1.5Ts，Ts为电流采样时间。

将式（4）和式（5）代入式（3），可得系统开环传递函数为

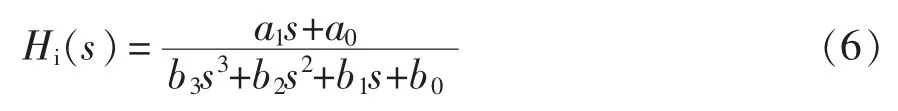
式中：a1=Kpiτi；a0=Kpi；b3=TdL；b2=TdR+L；b1=R；b0=0。

由式（6）可知，电流内环开环传递函数为3阶系统，若要使电流内环达到期望的响应效果，需对电流内环控制器Gi（s）进行合理配置。本文利用MATLAB/SISO设计工具，在电路参数确定的情况下，通过对Gi（s）零点与增益的合理配置使电流响应达到期望的控制效果。

探究电流控制器Gi（s）零点和增益分别对系统性能的影响，首先保持增益值不变，改变零点位置得到电流内环开环Bode图，如图9所示。由图9（a）所示，当零点从中频段向低频段移动时，τi减小，相位裕度增加，截止频率减小；由图9（b）所示，当零点移动到低频段时，相位裕度下降至24.3°，无法满足稳定性需求；由图9（c）所示，当零点移动到高频段时，增益裕度为2.21 dB，相位裕度为0.369°，无法满足工程设计需求。为保证电流内环的稳定性以及快速性，在中频段取τi=0.021。

图9 参数τi变化时电流内环开环Bode图Fig.9 Bode diagram of inner current open-loop with different values of τi

对于Kpi值的选取，根据自动控制理论[20]，在τi一定的情况下，增大Kpi可以加快响应速度，增加系统带宽，但Kpi增大也会引起超调量增大，降低系统稳定裕度。综合电流内环的稳定性和快速性，本文选取电流控制器的参数为Kpi=1 000，τi=0.021得到如图10所示的电流内环开环Bode图和闭环Bode图。如图 10（a）所示，此时系统相位裕度为 50.3°，截止频率为872 Hz，在中频段穿越0 dB线，同时保证了系统的稳定性和快速性，满足设计需求。如图10（b）所示，系统闭环Bode图的频带宽度（-3 dB处）为1.13 kHz,约为开关频率的1/10。在带宽内幅值增益为0 dB，保证了对带宽内信号的复现，在大于带宽的频段范围以-40 dB斜率衰减可以有效抑制高频干扰，同样是满足设计需求的。

2.2 电压外环控制系统设计

电压外环控制框图如图11所示，1/（Tss+1）为电压外环采样时间延迟，iL为负载电流干扰项，Gv（s）为电压外环控制器传递函数，表示为

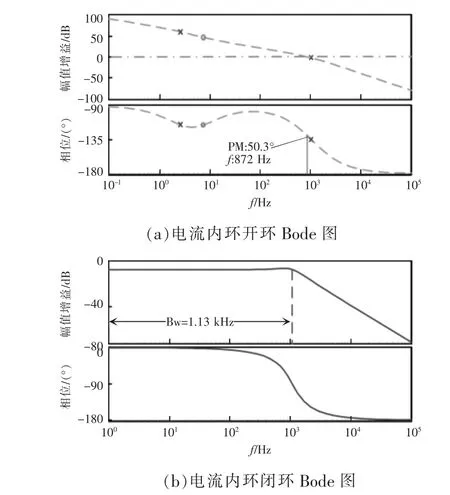
图10 补偿后电流内环开环与闭环Bode图Fig.10 Bode diagram of inner current open-loop and

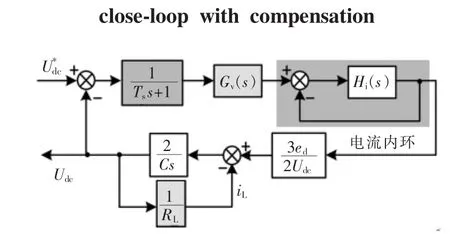
图11 电压外环控制框图Fig.11 Block diagram of outer voltage loop control

当开关频率远大于电网频率时，即Ts足够小时，电流内环传递函数可用1阶惯性环节等效，即

将电压外环采样时间延迟与电流内环传递函数合并并忽略高次项S2，同时忽略负载电流iL干扰,可得简化控制框图如图12所示。

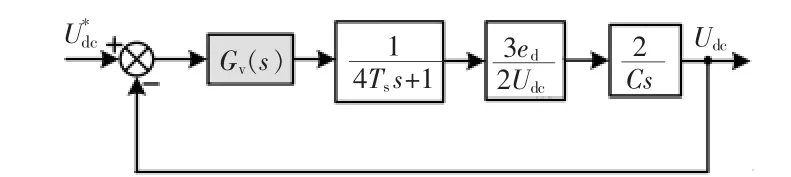
图12 电压外环简化控制框图Fig.12 Simplified block diagram of outer voltage loop control

为避免电压外环与电流内环的相互干扰，应尽量使电压外环带宽远远小于电流内环带宽。同时，相比与电流内环满足快速跟踪性，电压外环更注重稳定性，主要着重于系统的抗干扰能力。采用与电流内环相同的设计方法，利用MATLAB/SISO设计工具，对电压外环控制器零点和增益进行合理配置并分析不同负载RL对系统稳定性的影响，满足设计需求。

当电压外环控制器参数Kpv=50，τv=0.035时，电压外环开环Bode图和闭环Bode图如图13所示。由图 13（a）所示，此时相位裕度 75.1°，截止频率82.7 Hz。由图 13（b）所示，系统带宽为 110 Hz。满足电压外环设计需求。

当考虑负载电流对系统干扰时，电压外环开环Bode图和闭环Bode图如图14所示。开环相位裕度75.9°，截止频率81.7 Hz，闭环频带宽度 105 Hz。即使在有负载电流干扰的情况下，系统依然能保持稳定，符合设计需求。

由电压外环控制框图可得电压外环的开环传递函数为

图13 补偿后电压外环开环与闭环Bode图Fig.13 Bode diagram of outer voltage open-loop and close-loop with compensation

图14 负载电流iL干扰下的电压外环开环与闭环Bode图Fig.14 Bode diagram of outer voltage open-loop and close-loop with load current disturbance iL

3 系统仿真与结果分析

为验证VIENNA整流器双闭环控制策略以及参数设计的正确性，利用MATLAB/Simulink软件搭建VIENNA整流器仿真模型。仿真参数选取见表1。

表2给出额定负载下整流器的指标。图15为额定负载稳定运行下的仿真结果。图15（a）所示为网侧A相电流跟踪网侧A相电压的波形，图15（b）所示为直流侧电压波形，图15（c）额定负载下的功率因数大于等于0.995，图15（d）所示，网侧电流总谐波畸变率（THD）为1.81%。均符合技术指标。

图16分别给出了负载功率在7.5 kW和3.75kW之间动态切换的网侧电流、电压波形和直流侧的电压波形。由图 16（a）和图 16（c）可见，在负载动态切换过程中，网侧电流波形无畸变，并继续保持单位功率因数运行，由图 16（b）和图 16（d）可见在负载动态切换过程中，直流侧电压能迅速从波动中恢复稳定。证明了设计参数的正确性。

表1 VIENNA整流器主要参数Tab.1 Main parameters of VIENNA rectifier

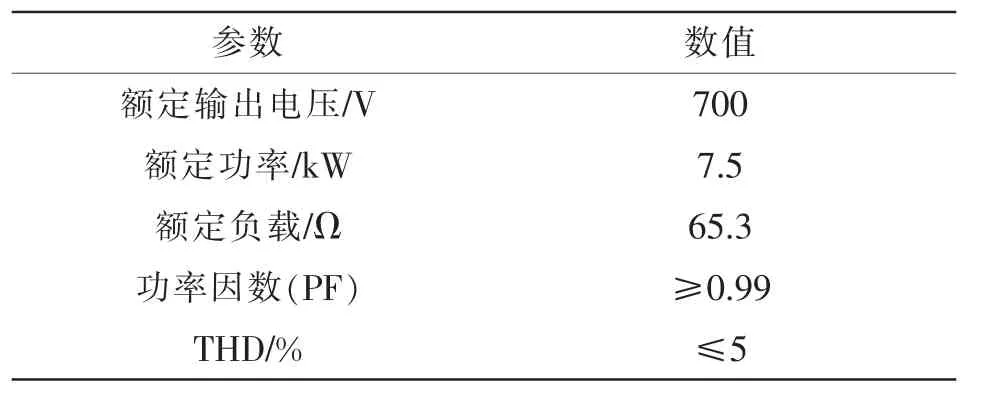
表2 VIENNA整流器技术指标Tab.2 Technical indexes of VIENNA rectifier

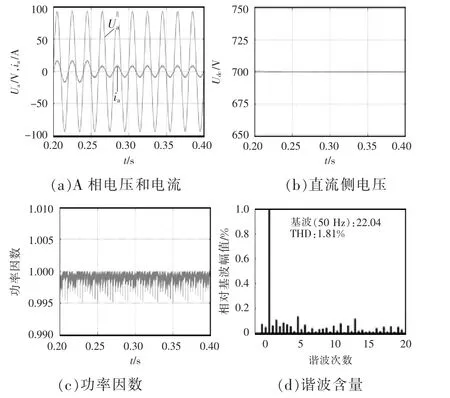
图15 额定负载稳态运行下仿真结果Fig.15 Simulation results of steady-state operation under rated load

图16 负载由7.5 kW突变到3.75 kW时动态切换仿真结果Fig.16 Simulation results under load dynamically changing from 7.5 kW to 3.75 kW

针对三电平变换器中点电位波动的问题，本文采用的是在空间矢量调制中运用正负小矢量抵消的方法来平衡中点电位，如图17所示。

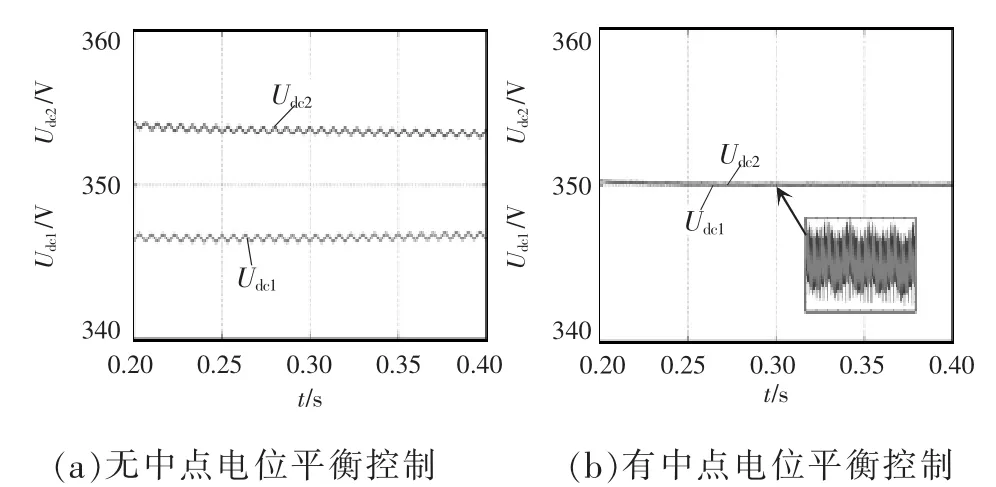
图17 直流侧中点电位仿真波形Fig.17 Simulation waveforms of midpoint potential on DC side

4 结语

通过对VIENNA整流器的分析，利用前馈解耦控制策略，建立了d-q坐标系下的数学模型。为实现有功、无功功率的独立控制，设计了电流内环、电压外环的双闭环控制策略，并利用MATLAB/SISO设计工具对电流和电压环控制器零点位置和环路增益进行优化配置，提高系统动静态特性，验证了不同负载电流干扰对电压环稳定性影响，最后，通过MATLAB/SIMULINK仿真验证了电流环和电压环控制器参数设计的正确性与合理性。