基于单周期控制的三相VIENNA整流器中点电压平衡控制策略
2018-10-10许冠军
许冠军,王 聪
(中国矿业大学(北京)机电与信息工程学院,北京 100083)
VIENNA整流器是一种三电平单向变换器,具有较强的功率因数校正PFC(power factor correction)以及交流侧电流谐波抑制能力,而且功率器件所承受电压均为输出电压的一半,可使用廉价的低压器件,并能减少开关管数量,降低成本,精简控制电路实现单位功率因数整流,故理论上具有更高的系统效率[1-3],因此在航空供电系统、通信设备以及新能源等众多领域得到广泛的应用[4-6]。
单周期控制 OCC(one-cycle control)是一种新颖的非线性控制方法,其特点为:无需采样交流侧电压,无需乘法器,控制电路简单,经济成本较低,但由于单周期控制直接以输入电流的基波作为调制波,因此输入电流波形质量的好坏直接决定系统控制效果,尤其在负载轻载下,输入电流中含有一定低频纹波,会对系统造成一定的影响。近年来单周期控制凭借其优势得到了广泛关注,并被应用于有源电力滤波器、PFC和开关功率放大器等领域。
中点电位波动是中点箝位NPC(neutral point clamped)结构变换器固有的问题。对于三电平变换器而言,中点电位交流波动,不仅会导致输出电压谐波增大,而且会损坏开关器件和输出侧电容,从而对变换器的稳定运行产生较大的安全隐患。针对这一问题,学者们提出了许多解决方案,主要包括硬件和软件两个方式。对于硬件方式则是通过电路结构上的改进来实现,而对于软件方式主要从控制策略上进行改进,主要分为两类,一类是基于空间矢量脉宽调制的方法,另一类是基于载波脉宽调制的方法。文献[7-8]多是通过重新分配冗余小矢量的作用时间来实现中点电压平衡,但控制策略的算法复杂,运算量较大,应用起来比较困难;文献[9-10]多是通过向控制系统中注入零序分量来维持中点电压平衡的控制策略,但是零序分量具体量计算非常繁琐,不易于应用且会增加成本;文献[11]针对三电平中点电压问题提出了一种基于载波变幅的SPWM调制策略,有效地实现对中点电压平衡控制,但调节时间较长且控制较为复杂,实现起来具有局限性。而对于采用单周期作为控制策略的VIENNA整流器,直流侧电容中点电压平衡控制的研究较少。其中文献[12]在单周期控制的基础上提出了一种向三相输入电流中注入3次谐波分量的方法,虽然起到抑制中点电位波动的作用,但需要基于输入电流进行三相正弦波交割构造3次谐波,从而增加了其控制复杂程度,使得该控制策略应用起来具有一定的局限性;文献[13]采用扩展状态空间平均法进行建模分析,计算出了影响中点电压平衡的零序分量,同时采用模拟电路来实现控制,取得了一定的效果,但却没有从理论上给出所注入零序分量的具体含量以及对中点电压平衡的具体影响。
本文首先对中点电压波动问题进行建模分析,计算出中点电压平衡的最佳零序分量。在单周期控制的基础上从直流侧上、下两电容电压之差中引入3次谐波,作为零序前馈补偿和中点电压差反馈控制,将其视为中点电压平衡控制环,并从理论上证明了该控制产生的零序分量近似为最佳零序分量,并给出了中点电压波动与输入电流幅值的比例关系。这不仅可以抑制中点电位交、直流波动,而且还能提高直流侧母线电压利用率,减少交流脉动和畸变。最后通过仿真验证了所提出的控制策略的正确性。
1 三相VIENNA整流器传统单周期控制
为了简化推导过程,本文做出如下假设:①线路阻抗为0,三相电压对称;②开关频率远远大于工频;③电路中各器件均为理想器件,均无损耗。
1.1 拓扑结构
三相三电平三开关VIENNA整流器电路拓扑如图1所示。其拓扑结构主要包含:3个升压电感La、Lb和 Lc(La=Lb=Lc=L);3 个全控型器件(MOSFET)Qa、Qb和 Qc,且各与 2 个快恢复二极管(Dj+和 Dj-,j=a,b,c)和4个二极管组成的整流桥相结合;2个足够大的输出电容C1和C2。

图1 三相VIENNA整流器拓扑Fig.1 Topology of three-phase VIENNA rectifier
1.2 传统单周期控制
单周期控制的根本目的是使输入电压与输入电流同相位,根据PFC本质定义可知,输入电压与输入电流关系为

式中,Req为各相输入阻抗的等效电阻。由文献[14]可知,单周期PFC的三相VIENNA整流器核心控制方程为

式中:Rs为电流采样增益;Um为稳态时电压控制器输出值,Um=U0Rs/2Req;Da、Db、Dc分别为全控型器件Qa、Qb、Qc的导通占空比。
将Um代入式(2)变换可得三相VIENNA整流器输入电压与直流侧输出电压的关系为

式(3)表明,当采用传统单周期控制策略时,整流器输出电压应大于交流侧输入电源相电压峰值的2倍,否则会造成整流器直流母线电压利用率不足,使得系统出现过调制,导致输入电流产生畸变。而对于在通信电源等应用系统中,通常会在整流器后级接入DC/DC变换器进行直-直变换。当其前级输出电压较高时(即DC/DC变换器输入),对后级DC/DC变换器的工作效率会造成一定影响,从而最终降低了整个系统的效率。因此,非常有必要提高VIENNA整流器直流母线电压利用率。传统的数字单周期控制其控制电路示意如图2所示,图中并没有针对中点电位波动问题进行控制。

图2 传统单周期控制示意Fig.2 Schematic of conventional OCC
2 中点电位平衡控制策略研究
2.1 中点电位交流波动分析
中点电位波动是NPC结构变换器固有的问题,当系统采用单周期控制时,三相VIENNA整流器输出电容中点电流的低频分量为3倍于输入电源基波频率的交流信号,会造成电容中点电位产生交流波动。因此,为了消除中点电位交流波动,就需要消除输出电容中3倍于输入电源基波频率的交流波动。所以可以通过向开关函数中引入零序分量来控制中点电位平衡。
参考直流侧中性点M的整流器输入端电压UjM三相开关函数的基波可表示为

式中:MF为调制比;ω0为输入电源基波角频率。
该整流器的三相输入电流基波表示为

式中,IM为三相输入电流基波幅值。
则核心控制方程式(2)可表示为

当在传统单周期控制中引入中点电压控制环后,相当于在三相桥臂中注入了零序分量,此时实际的开关函数基波为

式中,S0为各开关函数基波中的零序分量。
对于三相VIENNA整流器而言,参考直流侧中性点M的整流器输入端电压(UjM)由三相桥臂开关状态和相电流的方向共同决定。当某相桥臂开关状态为导通时,周期性的相电流将导致电容电压的不均。因此,VIENNA整流器的中点电流的平均值在一个调制周期中可表示为

在稳态情况下,为了完全消除中点电位的交流波动,中点电流ineu应一直保持为0。因此,设计的中点电压平衡控制环所注入的零序分量应为
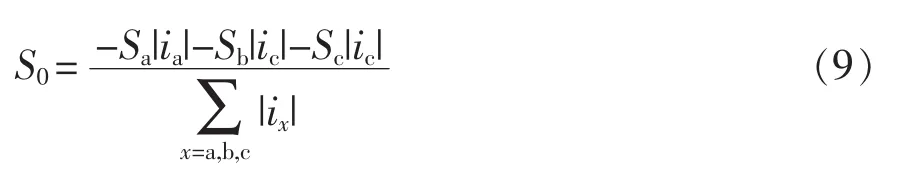
由式(9)可得零序分量为

式(10)表明,当其开关函数中含有零序分量为 S0(opt)时,其整流器的中点电位交流波动基本被消除。
2.2 中点电压平衡控制器设计
由前文分析可知,输出侧上、下两电容电压之差(UC1-UC2=ΔU)中也存在3倍于电源基波频率的交流信号,该控制策略的思想就是将其引入中点电压平衡控制环中,从而在开关函数中产生零序分量达到消除电容中的交流波动目的。输出侧电容电压之差与中点电流的关系表达为

假设 S0=S'0+ΔS0,则 S'0可表示为

由式(8)、式(11)和式(12)可得

所以直流侧2个电容间的电压差值ΔU和零序分量S0之间的传递函数为

假设 ia、ib、ic均为标准正弦波形,则

则式(14)可化为

式(16)所示为1阶惯性环节,控制中可用PI控制器H1(s)=kP1+kI1/s来实现其函数功能。其控制框图如图3所示。
在单周期基础上加入中点电压平衡控制环后,结合式(6)和式(7),改进后的单周期控制策略核心方程式为

图3 零序分量PI控制器控制框图Fig.3 Control block diagram of zero-sequence component PI controller

式中,ΔUm为中点电压控制电路PI控制器输出值,与采样输入电流幅值为定值比例关系,表示为

式中,RsIM为采样输入电流的幅值。
由式(6)、式(7)、式(17)和式(18)可得

通过比较式(10)和式(19)可知,中点电压平衡控制环可在三相桥臂中产生最佳零序分量,从而完全抑制中点电压交流波动。
由式(16)可知,本文中点电压平衡控制环为一阶惯性环节,从而也可以采用比例调节器(P调节器)来实现。则上、下两电容之差ΔU与采样的输入电流幅值关系为

由式(20)可知,通过调节比例环节系数kp可以具体控制中点电压波动幅值,将其控制在合适范围中,保持电容电压中3次谐波波形完好,从而更加有效地提高直流母线利用率。
采用改进单周期控制策略后,则式(3)为
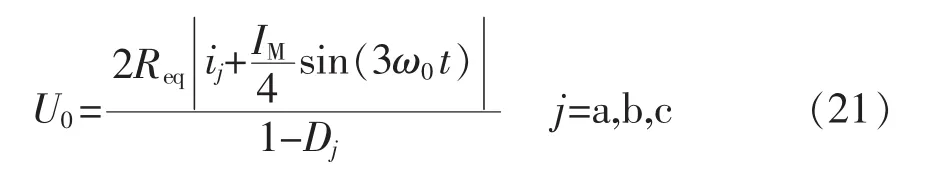
由上述分析可得:采用改进的单周期控制策略后,中点电压采样值经均压环调制后与输入电流采样叠加得到鞍形调制波形,其叠加后单位化的原理图如图4所示。
由图4可知,在相同的输入条件下,相比正弦调制波,将获得的鞍形波作为调制信号与三角载波进行交割产生PWM信号,所获得调制波幅值要低于原调制波,从而能获得更低的输出电压。可见该控制策略不仅可以进行中点电位平衡,还能在一定程度上提高直流母线利用率。因此改进后的单周期控制原理如图5所示。

图4 鞍形调制波形的生成原理Fig.4 Generating schematic of saddle modulation waveform
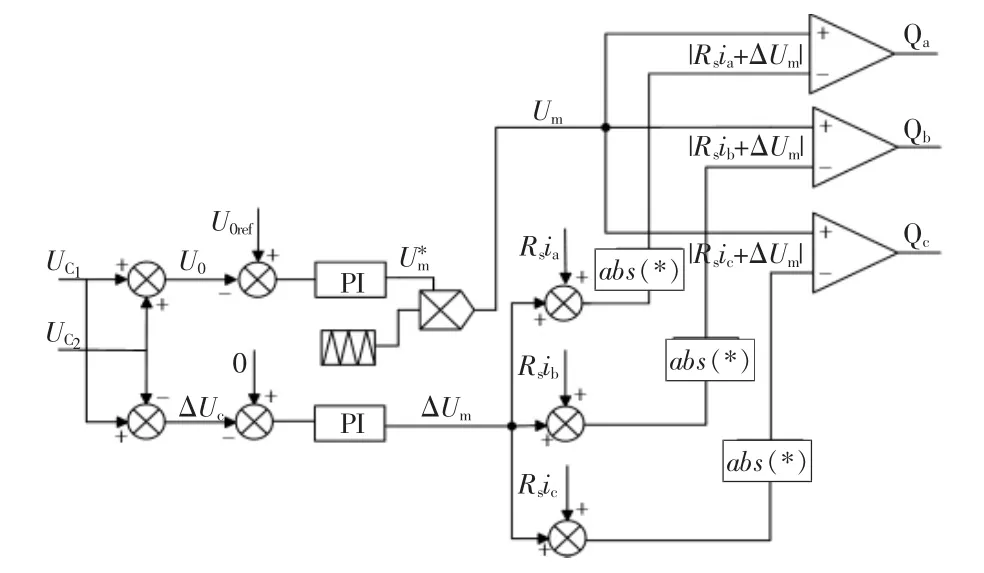
图5 三相OCC控制器结构框图Fig.5 Block diagram of structure of three-phase OCC controller
3 仿真验证
3.1 参数介绍
针对上述分析,本文对三相VIENNA整流器进行仿真研究。其主要仿真电路参数如下:三相输入电压380 VAC/50 Hz;输出直流电压600 V;额定输出功率为10 kW;负载等效电阻36 Ω;开关频率50 kHz;三相输入电感1.8 mH;直流侧2个输出电容为2 200 μF。负载轻载下输出功率为2.4 kW;负载等效电阻150 Ω;其他参数保持不变。
3.2 系统仿真研究
图6为输入电压和输入电流波形,可以看出输入电压与输入电流基本满足同相位关系且波形完好,由FFT分析知电流的THD约为2.5%,基本实现了单位功率因数。

图6 输入电压和输入电流波形Fig.6 Waveforms of input voltage and input current
图7为两种控制方式下电容电压波形,对比图7(a)和(b)可知,加入中点电压平衡控制策略后的单周期控制可以很好地抑制输出电容电压中的交流脉动信号,而且电容电压保持良好的均压状态。图8为A相桥臂开关函数及零序分量仿真波形,结果表明该控制下的零序分量S0基本与理论值S0(opt)相同。图9为不同控制策略下输入电流ia和参考直流侧中性点M的整流器输入端电压UaM仿真波形(不同控制策略下系统各参数保持一致,输出电压同为600 V),其中图9(a)表明在传统单周期控制策略下系统会出现过调制,输入电流波形尖端失真,图9(b)表明采用新型控制策略则可以消除过调制现象,输入电流波形完好,从而能在一定程度上提高直流母线利用率。图10为负载跳变时输入端三相电流波形,其中图 10(a)、图 10(b)分别为0.5 s时负载突卸和在0.6 s时负载突加时的输入电流波形。由图10可以看出,当负载发生跳变时,输出电流波动较小,并且在1~2个电网周期就能达到新的稳态,说明系统具有良好动态性能且负载变化对系统稳态运行影响不大。
负载轻载下的仿真结果如图11所示,分别表示为三相输入电压、三相输入电流和电容两端电压。由图 11(a)和图 11(b)可见,负载轻载下三相输入电压与三相输入电流基本满足同相位关系;由FFT分析可知电流的THD约为3.8%,波形质量较好,验证了本文所提的控制策略可实现单位功率因数。由图11(c)可见,电容两端电压UC1和UC2的波动值较小,表明采用新型控制策略可实现中点电压平衡。因此,本文所提出的基于单周期控制的中点电压平衡控制策略在负载轻载下依然具有良好的效果。

图7 不同控制方式下的输出电容电压Fig.7 Output capacitor voltages in different control modes

图8 A相桥臂开关函数及零序分量Fig.8 A-phase bridge arm switch function and zerosequence component

图9 不同控制方式下的输入电流ia电压UaMFig.9 Input current iaand voltage UaMin different control modes

图10 负载跳变波形Fig.10 Waveforms of load jump

图11 负载轻载下的仿真结果Fig.11 Simulation results under light load
4 结语
针对三相VIENNA整流器中点电位的交流波动问题,本文首先对其中点电位波动问题进行建模分析,提出了在传统的单周期控制基础上引入中点电位平衡控制环的控制策略,该控制策略不仅可以消除中点电位交流波动,使输出电容很好地保持均压状态,还可以提高直流侧母线电压利用率,并且系统具有良好的动态响应性能。仿真结果表明了该控制策略理论分析的正确性。
