新型解耦控制的级联型整流器控制策略
2018-10-10李秋思乔美英
郑 征,李秋思,乔美英
(河南理工大学电气工程与自动化学院,焦作454000)
级联型变换器已广泛应用于大功率电机传动、高压大功率电源、固态变压器和高压大功率无功补偿器等场合[1]。目前常见的多电平变换器大致可以分为二极管钳位型、飞跨电容式多电平变换器和级联H桥式多电平变换器。在多电平变换器拓扑结构中,级联H桥多电平拓扑在输出同样的电平数时所需要的开关器件少,具有很强的拓展性和灵活性,容易实现模块化和集成化[2-3]。
直流侧电容电压不平衡一直是多电平变换器研究的核心问题。所选器件参数不匹配、开关损耗、各桥臂开关延时和负载不平衡等因素将会影响级联H桥直流侧电容电压平衡。直流侧电容电压不平衡将会导致输入电流畸变、各个功率单元功率损耗不平衡和增大输出电压谐波畸变率,严重时将会导致整个系统崩溃。在变换器直流侧连接各种负载,且自身工作在整流状态时,这种问题将更为严重。因此,直流侧电压平衡能力对一个稳定可靠的系统是非常重要的性能指标。
由于单相级联H桥电路拓扑结构在实现单相旋转坐标变换时存在局限性,本文采用虚拟H桥与真实H桥相结合的改进型电路拓扑结构。针对两级级联H桥整流器直流侧电压平衡控制,考虑到级联整流器本身非线性特性,在单相旋转坐标系下建立系统小信号模型,对输入侧交流合成电压进行解耦控制,减小电压平衡控制器与系统自身耦合作用。同时,结合二维调制算法来实现各桥直流侧电压平衡和提高系统动态性能指标。
1 级联H桥整流器数学模型
1.1 传统系统数学模型
单相两级级联整流器拓扑结构如图1所示。us、is分别是输入侧交流电压和交流电流;R是交流回路等效电阻,为线路内阻、开关损耗电阻与电抗器电阻之和;L是交流侧输入滤波电感;Ci、Ri和udci是第i(i=1,2)个功率单元直流侧母线电容、等效负载阻值和直流母线电压;ucon是级联H桥交流侧合成电压。
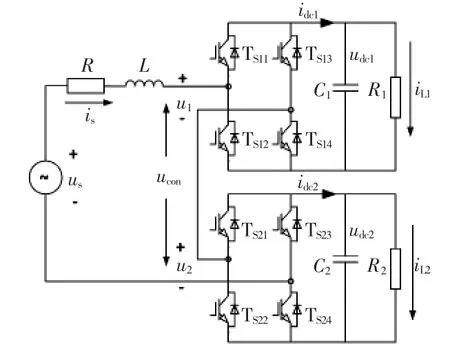
图1 单相两级级联整流器电路拓扑结构Fig.1 Topology of single-phase two-level cascaded rectifier circuit
该拓扑基于占空比的数学模型[4-5]为

式中:di为第i个功率单元的占空比,其取值范围为[-1,1]。
文献[5]为实现单相旋转坐标变换,对交流侧输入电流is构造超前正交虚拟变量im。为实现输入交流侧单位功率因数运行,假设交流侧合成电压ucon与输入电流is同相位。文献[5]采用相关变量的时域表达式为

式中:Im、Um分别为输入电流和输入电压的幅值;ω为交流电源的角频率;φ为电流滞后电压的相位角;ucond和uconq为交流侧合成电压ucon在单相旋转坐标系下的正交分量。
由式(1)和式(2)可得单相两级级联整流器在单相旋转坐标系下的数学模型为

从式(3)可见,id和iq相互耦合。对单相两级级联H桥整流器系统在单相旋转坐标系下的数学模型进行前馈解耦控制,可得解耦控制框图[5],如图2所示。

图2 传统解耦控制框图Fig.2 Block diagram of the conventional decoupling control
1.2 改进系统数学模型
传统数学模型并未给出d-q坐标系下 ucond和uconq与各功率单元占空比的直接关系,未考虑到各功率单位占空比波动对系统的影响,为此对系统电路拓扑结构进行改进。单相两级级联H桥整流器带虚拟H桥电路拓扑结构如图3所示。其中,单相两级级联H桥整流器拓扑结构如图3左侧实线所示;为了实现单相系统d-q变换,假设有2个与原H桥对称的虚拟H桥[6],如图3右侧虚线所示。
在幅值上,虚拟H桥参数变量与真实H桥变量相等;在相位上,虚拟H桥参数变量超前真实H桥变量90°。虚拟和真实H桥参数变量下标分别用m和s表示,则虚拟H桥变量与真实H桥变量在两相静止坐标系下的关系如图4所示。
现定义开关函数如下:


图3 单相两级级联整流器带虚拟H桥电路拓扑结构Fig.3 Topology of single-phase two-level cascaded rectifier with virtual H-bridge circuit

图4 虚拟变量与真实变量在两相静止坐标系下关系Fig.4 Relationship between virtual and real variables in a two-phase static coordinate system
对图3应用基尔霍夫电压定律和电流定律,可得系统在静止坐标系下的状态空间方程[6]为
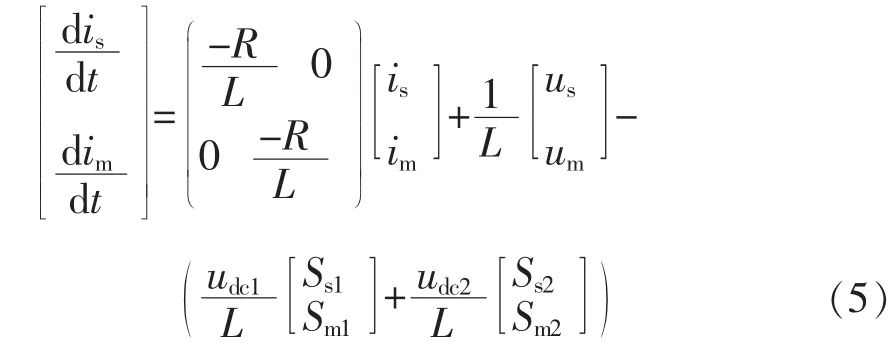
开关函数可以精确地描述整流器的性质,但是高频分量给控制器的设计带来许多困难。当开关频率远大于基波频率时,可以只考虑开关函数的低频分量,从而获得基于占空比描述的低频数学模型。利用傅里叶分解可以分离开关函数中的高频分量和低频分量。当开关频率远高于电网基波频率时,采用规则采样法,利用傅里叶分解得到开关函数低频分量的等效形式为

将式(6)代入式(5),得到系统在静止坐标系下基于占空比的数学模型为

为简化控制系统设计,现在只考虑开关函数的低频分量。本文取相关参数变量的时域表达形式为

由式(8)可得系统从静止坐标系到旋转坐标系的坐标变换公式及其反变换矩阵,即

根据式(8)~式(10),则式(7)在单相旋转坐标系下的数学模型为

式中,ddi、dqi分别为级联H桥各桥的有功功率占空比和无功功率占空比。
为实现输入侧单位功率因数运行,当ucon与is同相位时,级联整流器在单相旋转坐标系下的数学模型可用式(3)表示。对比式(11)和式(3)可得
当输入侧单位功率因数运行时,两级级联H桥整流器在d-q坐标系下的小信号模型如图5所示。

图5 两级级联整流器在d-q坐标系下的小信号模型Fig.5 Small-signal model of two-level cascaded rectifier in a d-q coordinate system
2 前馈解耦控制
由式(12)可以看出,ucond和 uconq与直流母线和各功率单元的占空比有直接关系,利用此关系可控制输出侧直流母线电压。同时,由级联整流器在d-q坐标系下的小信号模型可以发现,当级联H桥直流母线电压udci或各功率单元占空比发生波动时,ucond和uconq都将会受影响,从而影响系统性能。因此,文献[5]利用传统解耦方式,并未考虑到系统自身非线性和变量之间的耦合作用。式(12)变为


此时,ucond和uconq与各桥占空比呈比例线性关系。由式(13)和式(14)可知,直流侧电压不平衡时产生的附加电压为。考虑到级联H桥自身非线性特性,应减小参数之间耦合效应,此时需要对ucond和uconq进行解耦控制。因此新的电压平衡控制的关键是尽量减小附加电压的幅值。定义如下。

式中:Δddi为各桥有功占空比的调节修正值;Δudci为各桥输出侧直流母线电压与参考值之间的误差,其值由参考电压与反馈电压之间的差值经PI调节器得到。由于系统达到平衡时,q轴分量很小,因此将认为dqi=dq。减小系统变量之间的耦合效应,应使K1幅值尽量小。当K1幅值为0时,有功占空比[6]应满足

在单相旋转坐标系下,对级联H桥交流侧合成电压ucon进行解耦。系统达到平衡时,其数学模型为

将三相PWM整流器常用的前馈解耦控制方式引入到单相级联整流器控制中,系统解耦后可得

式中:kp和ki分别为电流内环PI调节器的比例和积分系数;i*d和i*q分别为由电压外环得到的id和iq的指令值。结合式(17)和式(18)可以得到单相两级级联整流器解耦控制框图,如图6所示。
3 二维调制平衡控制策略
从式(12)可知,在单相旋转坐标系下,输入交流侧合成电压ucon与直流侧输出电压udci和有功占空比ddi密切相关。因此,根据检测到的各桥udci与整流器交流侧在一个开关周期内合成的ucon,可计算出使两桥直流侧输出电压趋于平衡时的各桥占空比[13-15]。在脉宽调制技术方面,利用载波移相正弦脉宽调制技术调节各桥臂开关管的占空比,易于实现各个功率单元的能量均衡分布,减小系统谐波含量。
文献[4-5]均采用α1max和α'max调制曲线轨迹来实现直流侧电压平衡。本文在负载R1小于R2时,增加α2max调制曲线。在各种调制曲线下,各桥占空比如表1~表3所示。在负载R1小于R2时,采用α2max调制曲线和α'max调制曲线。在负载R1大于等于R2时,采用α1max调制曲线和α'max调制曲线。

图6 改进解耦系统控制框图Fig.6 Control block diagram of improved decoupling system

表1 采用α1max调制曲线的两桥占空比Tab.1 Duty ratio of H-bridges when α1maxmodulation curve is adopted
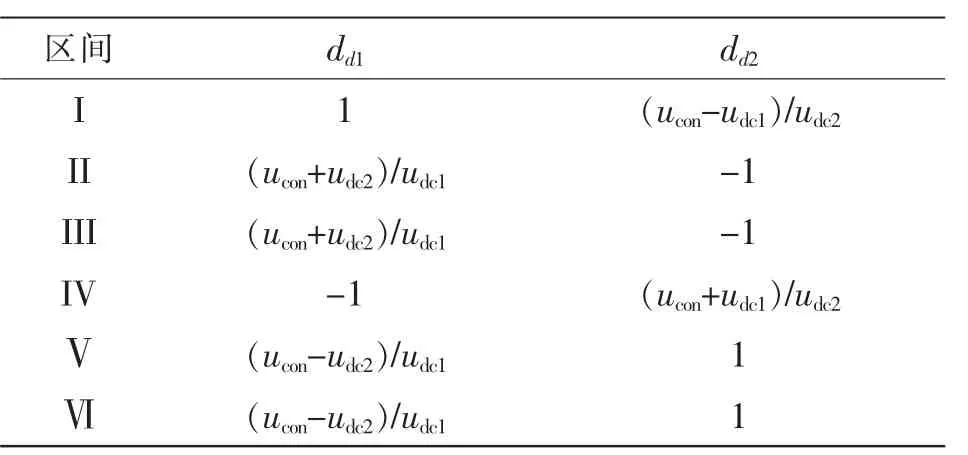
表2 采用α2max调制曲线的两桥占空比Tab.2 Duty ratio of H-bridges when α2maxmodulation curve is adopted

表3 采用α'max调制曲线的两桥占空比Tab.3 Duty ratio of H-bridges when α'maxmodulation curve is adopted
4 仿真与实验分析
4.1 仿真分析
为验证所搭建模型和使用控制策略对系统具有较好的动静态性能,将改进控制策略与传统控制策略进行对比。搭建了基于MATLAB/Simulink的仿真模型,仿真参数如表4所示。改进控制策略和传统控制策略下电压外环PI仿真参数相同,分别为kp=0.35,ki=23。

表4 仿真参数Tab.4 Simulation parameters
在等效负载 R1=200 Ω、R2=150 Ω 情况下,验证系统在负载不平衡情况下系统的动态性能和平衡能力。图7为改进控制策略下输入侧电压us与输入侧电流is波形。从图7可以看出,改进控制策略能够实现系统输入侧单位功率因数运行,提高系统效率。图8和图9分别为系统在改进控制策略下和传统控制策略下直流侧电压波形。从图8可得,直流侧电压进入稳定时调整时间为0.08 s,最大超调量18%;从图9可看出,直流侧电压进入稳定时调整时间为0.10 s,最大超调量42%。仿真结果表明,改进控制策略有效降低了系统超调量。
验证系统在负载不平衡情况下系统的抗干扰能力和稳定性。等效负载R2=150 Ω不变,R1在0.2 s时从130 Ω突变到30 Ω,在此情况下对比系统性能。图10是改进控制策略下的输出电压波形,在0.2 s时负载发生突变,直流母线电压依然稳定。图11是传统解耦控制策略下的输出电压波形,负载0.2 s突变后,电压udc1与udc2已经发生分离,此时传统电压控制策略已不能有效稳定直流侧母线电压。因此,改进的控制策略对系统具有较好的稳定性。

图7 负载不平衡时改进控制策略下单位功率因数运行Fig.7 Unity power factor operation under the improved control strategy when load is unbalanced

图8 负载不平衡时改进控制策略下启动电压Fig.8 Starting voltage under the improved control strategy when load is unbalanced

图9 负载不平衡时传统控制策略下启动电压Fig.9 Starting voltage under the conventional control strategy when load is unbalanced
4.2 实验分析
为进一步验证本文所提出控制策略的有效性,搭建基于RT-lab的实验平台,图12为实验系统描述框图。控制模型通过RT-lab产生功率单元的PWM脉冲信号,然后经过驱动电路来驱动IGBT工作。主电路采用的IGBT型号为F4-50R12KS4;驱动模块选为QP12W05S-37;电流检测回路采用型号为SN1T50C50V6的霍尔传感器。交流信号电源电压有效值为220 V,频率为50 Hz,开关频率5 kHz;交流输入侧电感10 mH;电容C1=C2=2.2 mF;输出直流参考电压为200 V。实验中输出直流侧电压udc1与udc2衰减20倍,交流侧合成电压ucon衰减800倍,电压us衰减310倍,电流is衰减20倍。

图10 改进控制策略下负载突变时直流侧电压Fig.10 DC-side voltage under the improved control strategy when load changes suddenly

图11 传统控制策略下负载突变时直流侧电压Fig.11 DC-side voltage under the conventional control strategy when load changes suddenly
等效负载 R1=200 Ω,R2=150 Ω,改进控制策略下的实验波形如下所示。图13为系统启动过程中输出侧电压udc1与udc2波形,系统启动中峰值电压为12 V,稳定后有效运行在10 V。图14为系统稳定运行时交流侧合成电压ucon,为5电平阶梯波。图15为系统输入侧电压us与输入侧电流is波形,表明系统能够实现输入侧单位功率因数运行。
同时,验证系统的抗扰动能力和稳定性。保持负载R2=150 Ω不变,在R1=130 Ω情况下启动,系统稳定运行后R1从130 Ω突变到30 Ω。两种控制策略在此情况下的实验波形如图16、图17所示。图16为改进控制策略下实验波形。由图可见,负载突变前输出侧电压udc1与udc2稳定运行在10 V;负载突变后,输出侧电压依然能够稳定输出。图17为传统控制策略下实验波形。由图可见,负载突变前输出侧电压udc1与udc2稳定运行在10 V;负载突变后,输出电压udc1与udc2逐渐分离。实验结果与仿真结果一致,改进控制策略对系统具有较好的稳定性。

图12 半实物实验系统Fig.12 Hardware-in-the-loop system

图13 启动时输出直流侧电压udc1、udc2波形Fig.13 Waveforms of DC-side voltages udc1and udc2 at startup

图14 交流侧电压ucon波形Fig.14 Waveforms of AC-side voltage ucon

图15 负载不平衡时us、is波形Fig.15 Waveforms of usand isunder unbalanced load

图16 改进控制策略下负载突变时udc1、udc2电压Fig.16 Voltages udc1and udc2under the improved control strategy when load changes suddenly

图17 传统控制策略下负载突变时udc1、udc2电压Fig.17 Voltages udc1and udc2under the conventional control strategy when load changes suddenly
5 结语
通过分析研究级联H桥整流器拓扑结构,建立了两级级联H桥在单相旋转坐标系下的小信号数学模型。在实现系统输入侧单位功率因数运行的基础上,对输入交流侧合成电压进行解耦控制,减小系统参数之间的耦合作用,提高直流侧电压响应速度。同时,结合二维调制平衡控制策略,增强系统的稳定性。仿真和实验都验证了所提出控制策略能够加快系统的调节速度和有效抑制输出直流侧电压超调量,提高了系统的静动态性能和系统稳定性。
