高中数学课堂中文化史的渗透

张溪珊

(福建省莆田市第十五中学 351131)

在讲授《数系的扩充与复数》这节内容时，我考虑到本节内容比较枯燥，如果直接平白地讲授，学生可能兴趣乏乏，假如在授课过程中能进行数系扩充小史的渗透，那学生的学习兴趣会不会被调动呢？“还是试试看吧，或许会有惊喜呢!”我告诉自己.

在课堂上，我首先给学生展示了这几个句子：平方得负岂荒唐？左转两番朝后方.加减乘除依旧算，方程有解没商量.立马引起了学生的兴趣，对这几句文字稍作解释后，我告诉学生人类认识数的范围是一步一步扩充的.到底是如何扩充的呢?

在PPT上给学生展示了这些内容：

1.自然数的原始概念在人类的文字尚未出现时即已形成.例如前人清点猎物的数目，拿过一只猎物(例如山鸡)就扳一个指头，或在一个小土坑里放上一颗石子，或在绳子上打一个结.这些事物的多寡都自然形成的，所以后人称其为自然数.据考古学家估计大约在5万年以前，有的甚至说30万年以前，人类已有自然数的概念.

2．公元元年左右，中国《九章算术》中由除法与减法引入了分数和负数.

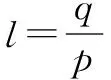
于是出现了第一次数学危机.

所以从那之后人们发现了一种不是自然数与分数的数，名曰“无理数”.数学家们把有理数与无理数统称为实数.到这里，数系已经扩充到了实数，学生的学习兴趣也被充分调动起来了.那么接下来引入问题.

问题1：如果把10看成某两个数的和，让这两个数的积等于40.

按照我们的思维习惯，设一个数为x，则另一个数为10-x，可列出方程为x(10-x)=40，得到一元二次方程x2-10x+40=0，这个方程有解吗？

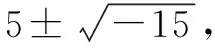
问题2：根据原有的知识体系，有没有这两个数？如果没有，怎么解决这个问题？

提示：方程x+1=0在正数范围内有解吗？如果没有，怎样让其有解？方程x2-1=0在有理数里有解吗？怎样让其有解的？

设计意图：让学生重新回顾数系的扩充，从(x-5)2=-15出发，思考-15开平方问题，即“负数开方”的问题怎么行得通.

问题3：要解决上面这个问题，就是要找到一个数，使得它的平方等于-15，那我们应该找一个怎样的数呢？我们找的这个数需要满足什么？

设计意图：引导学生再现卡丹问题，启发学生“引进一个新数，使其平方等于-1”.

问题4：大部分同学都已经预习了课本，知道引进了一个新的数i，它满足条件i2=-1，并且规定这个新的数i可以按照我们熟悉的运算法则以及一个新的法则i2=-1与实数进行运算，那你们知道为什么用i吗？

提示：i是英语单词“imaginary”(虚幻的)的第一个字母.

设计意图：向学生介绍虚数单位i的数学史，一方面加深学生对i的理解，另一方面让学生体会到数学发展的伟大与艰辛.让学生自己发现并“创造”出3i、-4i、5+6i、5-6i等.

问题5：(1)这些找到的新数可不可以用某个统一的数学符号或格式来表示呢？

(2)这些找到的新数构成的集合与我们学过的实数集又有怎样的包含关系呢？

设计意图：我们通过前面若干问题的铺垫，慢慢引导学生得出复数的代数形式，目的是为了培养学生上一章节学过的合情推理中的归纳数学思维能力.第二问是为了启发学生对复数进行分类，引入虚数、纯虚数的概念，可以让学生更深刻地理解本节的概念.

到这里，我们完成了复数概念的引入.

本节课我主要采用问题引入、启发的模式，几个问题层层相扣，逐步引导帮助学生在原有知识体系的基础上构建新的知识体系，这样新的知识的引入也就顺理成章，不再显得突兀了.

在整节课中，从介绍人类认识的数的范围的逐步扩充史到卡丹问题，再到欧拉引进虚数单位，让学生觉得数学发现并不神秘，数学课堂也并不枯燥，原来我们也有可能“创造新知”.这个过程极大地激发了高中生的创造热情，从而产生主动学习数学的热情，课堂效果自然显著.

数学文化是科学文化的重要内容，它不仅包含着数学知识，更教会我们用数学思想、眼光来观察问题、思考问题，而且还能提高我们的数学素养.

在接下来的实践教学中，我将把“以数学文化来育人、化人”作为教育目标，最后谨以屈原的名句“路漫漫其修远兮，吾将上下而求索”勉励自己.