关于高中数学中的数列问题的常用方法的总结

李 壮

(辽宁省铁岭县高级中学 112000)

一、数列通项公式的求法

1.累加法

适用于an+1=an+f(n)

例1 数列{an}对任意n∈N+，都有an+1=an+2n+1，a1=1，求数列{an}的通项公式.

解由题意，知

当n≥2时，a2-a1=2×1+1，

a3-a2=2×2+1，

…

an-an-1=2×(n-1)+1.

∴an-a1=2×[1+2+…+(n-1)]+n-1，

∴an=n2(n≥2).

又a1=1,∴an=n2，n∈N+

2.累乘法

适用于an+1=an·f(n)

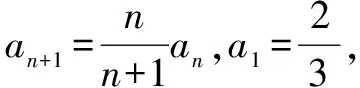
解由题意，知

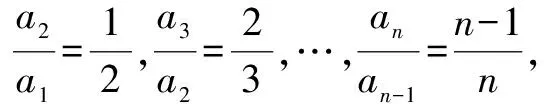
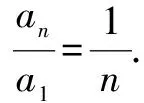
3.公式法

已知Sn，求an.

n=1时，a1=S1;n≥2时,an=Sn-Sn-1.

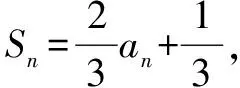
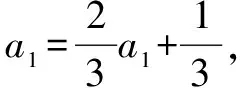
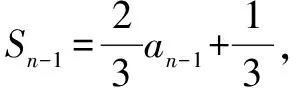
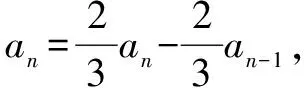
∴数列{an}是首项a1=1，公比q=-2的等比数列,

∴an=(-2)n-1.

4.待定系数法

适用于an+1=qan+f(n)

(1)形如an+1=can+d(c≠0,a1=a)

①若c=1,则数列{an}为等差数列；

②若d=0, 则数列{an}为等比数列；

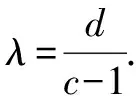
(2)形如an+1=pan+qn(pq≠0)

①若p=1,用累加法；

②若p≠1,用以下三种方法：

ⅰ.两边同时除以pn+1，再用累加法；

ⅱ.两边同时除以qn+1;

ⅲ.用待定系数法.

例4 数列{an}对任意n∈N+，an+1=2an+4×3n-1，a1=1，求数列{an}的通项公式.

(3)形如an+1=pan+kn+b(k,b是常数，且k≠0)

解题步骤：①确定f(n)=kn+b；

②设等比数列{bn}中bn=an+xn+y，公比为p;

③列出关系式an+xn+y=p[an-1+x(n-1)+y]，即bn=pbn-1；

④比较系数求出x,y;

⑤解出数列{bn}的通项公式；

⑥解出{an}的通项公式.

5.逐项相减法

例5 数列{an}对任意n∈N+，an+1=3an+2n，a1=1，求数列{an}的通项公式.

解∵an+1=3an+2n,∴an=3an-1+2(n-1),n≥2.

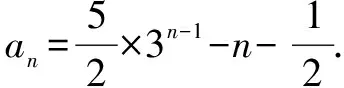
小结通过以上方法的总结和例题的解法可以看出它们是有内在联系的，既要注意一题多解，又要把握每个题型的特点.

6.对数变换法

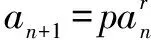
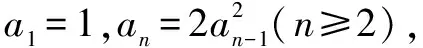
解两边取以2为底的对数，得log2an=1+2log2an+1=2(log2an-1+1).

令bn=log2an+1，则bn=2bn-1,数列{bn}为首项b1=1，公比q=2的等比数列，

可求得bn=2n-1，所以an=22n-1-1.

7.倒数变换法

适用于分式关系的递推公式,分子只有一项

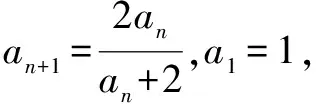
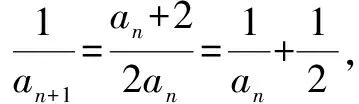
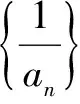
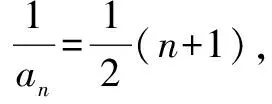
8.周期法

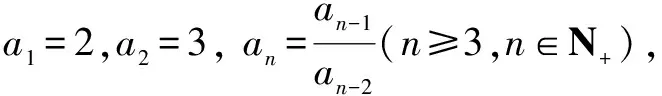
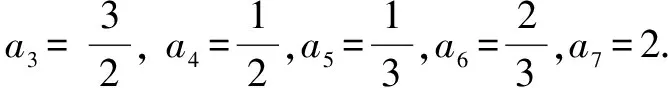
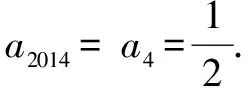
9.删项法

例9 数列{an}中，a1=1，对所有n≥2，n∈N+都有a1·a2·a3·…·an=n2，则a3+a5=( ).

解由题意，知a1·a2·a3·…·an-1=(n-1)2,n≥2.

二、数列求和

1.公式法

适用于等差数列和等比数列

例1 在等差数列{an}中，a16+a17+a18+a19=-36，其前n项和为Sn.

(1)求数列{an}的通项公式；

(2)求数列{an}的前n项和Sn.

2.分组求和法

例2 若数列{an}的通项公式为an=2n+2n-1,则数列{an}的前n项和为(C).

A.2n+n2-1 B. 2n+1+n2-1 C. 2n+1+n2-2 D. 2n+n2-2

3.裂项相消法

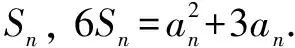
(1)求数列{an}的通项公式；

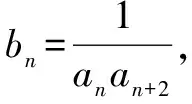
解(1)易求得an=3n.

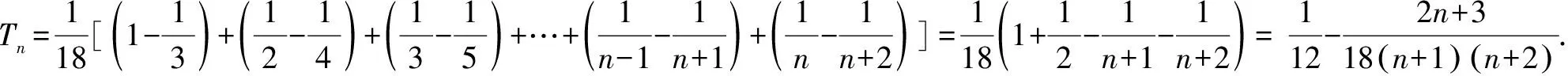
4.错位相减法

已知等比数列{an}满足a1a3=2a2，a5=16，单调递增的等差数列{bn}满足b2+b6=b3+5，b7=7.

(1)求{an}和{bn}的通项公式；

(2)设cn=anbn，求{cn}的前n项和Tn.

解(1)用公式易求得an=2n-1，bn=n.

(2)cn=anbn=n·2n-1，

∴Tn=1×20+2×21+…+n×2n-1,

∴2Tn=1×21+2×22+…+(n-1)×2n-1+n×2n.

两式相减，得-Tn=1+21+22+…+2n-1-n×2n=2n-1-n×2n,

∴Tn=(n-1)×2n+1.