基于连续介质假设原理的膨化机螺杆摩擦阻力分析及参数优化
2018-10-10卢进南
毛 君 鲁 楠 谢 苗 卢进南 贾 凯
(辽宁工程技术大学机械工程学院,辽宁 阜新 123000)
挤压膨化机因其独特的加工方式和输出结果,目前越来越受到饲料加工业和食品制造业的重视。通过挤压膨化技术处理的原料利用率通常能够达到80%甚至更多,因此大大地提高了产品的生产率和质量[1-2]。挤压加工技术最早出现在19世纪70年代的英国,并逐渐被应用到橡胶工业中[3],直到1936年第一台单螺杆挤压膨化机首次被意大利人应用于方便谷物食品生产中[4]。现如今挤压膨化加工技术己经非常普遍地应用于膨化玉米、大豆等谷物食品和饲料产品。但是如何不断提高膨化机的生产效率、降低能耗一直是国内外学者探讨的重点课题,现已成为膨化机研究的热点和关键问题。
近年来相关学者对如何优化挤压膨化机的设计进而提高设备的生产效率降低能耗进行了大量研究,但目前对挤压膨化机的优化研究仍略有局限性。张魁学等[5]通过正交多项式回归设计法研究分析了螺杆转速、物料温度以及工作压力等因素对机器生产率、耗电量、膨化率等的影响。邹凤等[6]利用动量定理推导出模孔径长比、物料与模孔壁间摩擦因数和模孔两端压强差三者间理论关系式。李少华等[7]以油菜籽为原料采用响应面分析法研究模孔直径、膨化温度、喂料速度和物料含水率对膨化预榨饼残油质量分数的影响规律,并对参数进行工艺优化。杨凯等[8]建立了同向啮合双螺杆挤压膨化机共轭型螺杆的力学模型及有限元模型,并运用有限元分析方法对不同螺距和内外径比(SAR)的螺杆进行了应力分析。这些研究多是通过试验分析方法从挤压膨化设备的模孔几何参数、物料含水率、螺杆转速、膨化温度、喂料速度等工艺参数对膨化机进行完善优化,进而提高挤压膨化机的生产效率降低能耗,而没有通过建立螺杆的摩擦力学模型然后运用数值分析法直观地分析螺杆多项结构参数对摩擦阻力的影响。鉴于目前对螺杆结构参数与螺杆摩擦磨损之间关系的研究缺陷,本研究将结合辽宁祥和农牧实业有限公司生产的9P-150B型秸秆膨化机,创新性地运用连续介质假设原理建立螺杆旋转挤压物料的摩擦阻力模型,进而对单螺杆秸秆膨化机的关键部件螺杆进行系统的摩擦受力分析,以降低有害摩擦进而提高螺杆的应力强度与膨化机的实用性能。
1 螺杆的构形要求及结构参数
1.1 螺杆的构形要求
针对挤压物料任务的螺杆主要功能:① 具备合理的结构参数以减小物料在挤压过程中与螺杆产生的磨损;② 具备良好的结构形态使物料在螺杆槽内能够得到充分的加工;③ 具备足够的刚度和强度以满足挤压物料过程中冲击振动等工况要求。本文主要针对物料与螺杆间产生的有害摩擦进行研究[9]。
1.2 螺杆的结构参数
对螺杆的摩擦阻力进行研究需要对其结构参数进行定义,以便建立其摩擦阻力的数学模型,螺杆结构参数见图1。
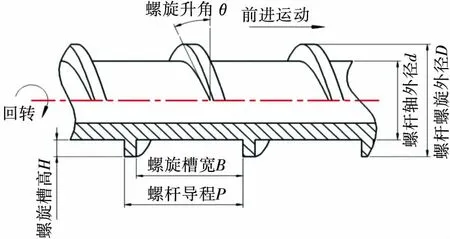
图1 螺杆结构参数示意图Figure 1 Schematic diagram of screw structure parameters
2 螺杆摩擦阻力分析及其力学模型的建立
秸秆在膨化机内的输送及挤压是一个相当复杂的过程,若运用连续介质假设原理进行理论分析,需要做出以下几点基本假设:
(1) 假定螺槽中运动的物料为可压缩的连续运动体,密度仅沿螺槽方向有变化。
(2) 螺杆中的物料与螺槽底面、两个侧面和机筒内表面同时紧密地接触,物料和螺槽各表面之间的摩擦力只取决于法向应力而与物料的位置和运动无关。
(3) 假设料筒在圆周方向上作匀速旋转运动,机筒相对于物料微元的运动方向角为φ,且忽略该夹角沿着物料运动方向的变化。
(4) 轴向应力(压力)和法向应力只沿物料运动方向变化。
基于上述的基本假设和分析,螺杆在旋转过程中受到物料产生的复杂摩擦力便可简化分成简单的两部分:① 物料在螺旋槽底面上产生的摩擦阻力;② 螺旋槽前后侧面与物料间产生的摩擦阻力[10]。
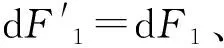

图2 物料在螺杆槽内的受力Figure 2 The force of material in the groove
2.1 物料在螺旋槽底面上产生的摩擦阻力
螺旋槽底面上物料微元产生的摩擦阻力:
dF1=fsdN1,
(1)
式中:
fs——物料与螺杆间的摩擦系数;
dF1——螺旋槽底面对物料微元的摩擦力,N;
dN1——螺旋槽底面对物料微元的支持力,N。
2.1.1 外机筒内表面对物料微元的压力 物料微元受到外机筒内表面的压力:
dN4=pBcosθdL,
(2)
式中:
p——外机筒作用于物料上的压力,Pa;
B——螺槽轴向宽度,m;
θ——螺杆螺旋升角,(°)。
查阅文献[12]可得,外机筒作用于物料上的压力与物料在加料斗处的初压力有关:
p=p0eτL,
(3)
式中:
L——计算段的螺槽长度,m;
p0——物料在加料斗处的初压力,Pa;
τ——比例系数。
由文献[12]得:
(4)
(5)
式中:
D——螺杆螺旋外径,m;
H——螺旋径向高度,m;
fb——物料与机筒间的摩擦系数;
φ——物料微元相对于机筒运动的方向角,(°)。
2.1.2 物料微元旋转运动时受到的离心力 物料在高速旋转时产生的离心力:
(6)
式中:
ρ(z)——物料密度,kg/m3;
ω——物料在螺杆螺旋槽内的转速,r/min。
式(7)中螺旋微元长度dL与轴向微元距离dz的关系:
(7)
2.1.3 螺旋槽底面对物料微元的支持力 由圆周运动受力平衡得:
dp+dN1=dN4。
(8)
所以
dN1=dN4-dp。
由式(1)~(8)得到:
(9)
2.2 物料在螺旋槽侧面上产生的摩擦阻力
物料微元在螺旋槽侧面上产生的摩擦阻力可分为前后两部分,分别为dF2与dF3。
dF2=fsdN2,
(10)
dF3=fsdN3,
(11)
dN3=dN2+dN0。
(12)
其中dN0为螺旋推力,螺旋前侧面法向作用力:
dN2=pHdL。
(13)
2.2.1 螺旋槽前侧面对物料微元的摩擦力 由式(3)、(7)、(10)、(13)得:
(14)
2.2.2 螺旋推力的计算 求F3需要知道dN0。将物料微元受到的所有力分解成沿轴向方向与沿螺纹螺旋方向,由于物料微元在螺旋槽中的运动是稳定的,因此沿轴向方向的所有分力的总和等于零,即
(15)
将式(12)带入式(15)得
dN0=dF4sin(φ+θ)。
(16)
又物料微元外表面上机筒产生的摩擦力:
dF4=fbdN4。
(17)
将式(17)带入式(16)得
dN0=fbdN4sin(φ+θ)。
(18)
2.2.3 螺旋槽后侧面对物料微元的摩擦力 由式(3)、(4)、(8)、(11)、(12)、(13)、(18)得:
(19)
由前述分析可知螺杆挤压物料受到的摩擦阻力为式(9)、(14)、(19)之和,即
(20)
3 螺杆结构参数与摩擦阻力关系影响分析
根据文献[13]可知,决定膨化机螺杆结构的参数主要有螺旋外径D、轴向槽宽B、径向齿高H以及螺旋升角θ。由式(20)可以很容易看出,螺杆受到的摩擦阻力随着螺杆螺旋外径D的增加而减少。螺旋外径增大说明螺杆在高速旋转下物料受到的离心力变大,导致螺杆底面对物料的挤压力变小,二者之间的摩擦力变小。而螺杆的其他参数(轴向槽宽B、径向齿高H、螺旋升角θ)对螺杆所受摩擦阻力的影响不能够轻易看出。因此采用Matlab分析其他参数对螺杆所受摩擦力造成的影响。
3.1 螺槽轴向宽度与摩擦阻力的关系
通过试验可以获得螺杆和机筒与物料间的摩擦系数fs=fb=0.3。则由式(20)可以得出,螺杆受到物料的摩擦阻力与螺杆轴向槽宽的数学关系如式(21)。
Ff=f(B)=F1(B)+F2(B)+F3(B)。
(21)
如图3所示,当螺槽轴向宽度增大时,螺杆受到的摩擦阻力呈增大趋势。螺槽轴向宽度增加说明螺旋槽容纳的物料更多,物料与螺杆的接触面积变大,摩擦阻力自然变大。但从图3中可看出,螺槽轴向宽度对螺杆受到的摩擦阻力的影响较小。
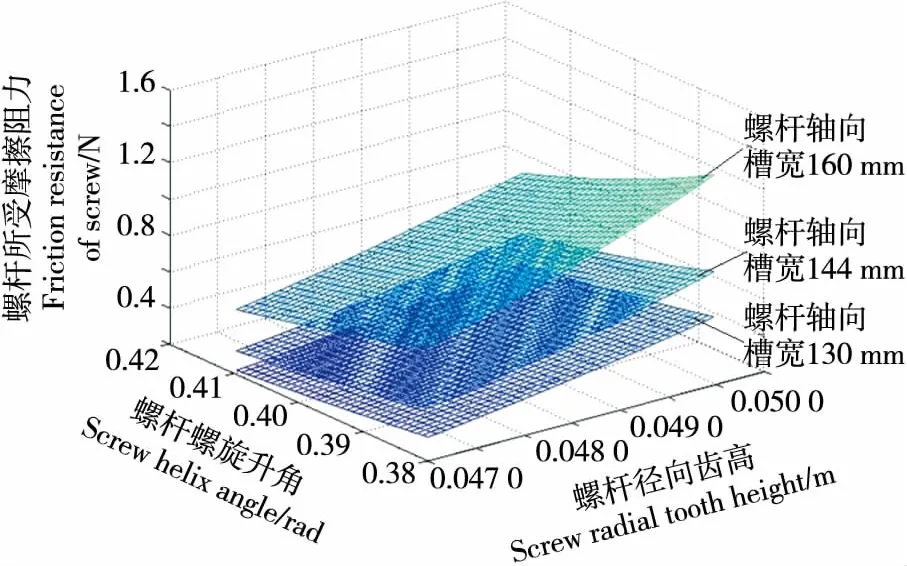
图3 螺杆摩擦阻力随螺旋升角和径向齿高变化关系
图3 Relationship between screw friction resistance and screw rise angle and radial tooth height
3.2 螺杆径向齿高与摩擦阻力的关系
由式(20)可以得出,螺杆受到物料的摩擦阻力与螺杆径向齿高的数学关系见式(22)。
Ff=f(H)=F1(H)+F2(H)+F3(H)。
(22)
由图4可知,螺杆所受摩擦力的绝对值随径向齿高的增加而增加。螺杆径向齿高增加,说明螺槽内的物料与螺槽侧壁的接触面积增大,因此螺杆所受摩擦力增大。相比于螺槽轴向宽度,螺杆径向齿对螺杆受到摩擦力的影响相对较明显。

图4 螺杆摩擦阻力随螺旋升角和螺旋外径变化关系
图4 Relationship between screw friction resistance and screw rise angle and screw outer diameter
3.3 螺杆螺旋升角与摩擦阻力的关系
由式(20)可以得出,螺杆受到物料的摩擦阻力与螺杆螺旋升角的数学关系见式(23)。
Ff=f(θ)=F1(θ)+F2(θ)+F3(θ)。
(23)
螺杆螺旋升角的大小影响机构工作时螺杆对物料的加工情况,螺旋升角过小时对物料的挤压比较充分,但需要消耗很大功率才将物料排出;螺旋升角过大时物料填充率不高,且物料受到的挤压不够充分。由图5可知,螺杆所受摩擦力随螺旋升角的减小而增大,且升角越小变化率越大,因为螺旋升角减小导致螺旋槽对物料的轴向分力变大,而径向分力减小,进而由轴向挤压力而产生的摩擦力随之变大。相比于轴向槽宽与径向齿高,螺旋升角的变化是对螺杆受到的摩擦力影响最为明显的一个因素。

图5 螺杆摩擦阻力随径向齿高和螺旋外径变化关系
图5 Relationship between screw friction resistance and radial tooth height and screw outer diameter
4 膨化机螺杆结构参数优化
4.1 目标函数
通过前文的分析可知,螺杆受到物料产生的摩擦力与螺杆的多项结构参数均有不同程度的关系,因此运用Matlab的optimization工具箱将螺杆的所有结构参数均考虑在内,以式(20)中各个结构参数乘以相应的权重系数所得的式(24)为目标函数,对螺杆进行结构优化使物料对螺杆产生的摩擦阻力有所降低。
Ff(X)=F(η1D,η2θ,η3B,η4H),
(24)
式中:
η1——螺杆螺旋外径权重系数;
η2——螺杆螺旋升角权重系数;
η3——螺杆轴向槽宽权重系数;
η4——螺杆径向齿高权重系数。
4.2 约束条件
建立螺杆结构优化的设计变量见式(25)。
X=(x1x2x3x4)T=(DθBH)T,
(25)
式中:
D——螺杆螺旋外径,m;
θ——螺杆螺旋升角,(°);
B——螺杆轴向槽宽,m;
H——螺杆径向齿高,m。
(1) 在实际生产中,弯曲力和扭矩力同时作用在螺杆上,但扭矩力要大于弯曲力,由材料力学可得:
(26)
式中:
[τ]——许用剪切应力,取340 MPa;
Nmax——电机最大额定功率,取110 kW;
μ——机械效率,取0.923;
nmax——螺杆最高转速,取157.1 r/min。
(2) 根据实际生产中对生产效率的要求可给出螺杆螺旋外径大致范围:
0.1≤D≤0.2。
(27)
(3) 螺旋升角范围:
10°≤θ≤30°。
(28)
(4) 由螺旋槽轴向宽度小于螺杆导程可得槽宽范围:
0.1≤B≤P=πtanθ(D-H)。
(29)
(5) 螺杆径向齿高小于螺旋外半径,则齿高范围:
(30)
4.3 螺杆结构参数优化数学模型
根据目标函数及参数约束条件的分析,可以将膨化机螺杆的尺寸参数优化问题确定为非线性约束的多目标最优化问题,选用Matlab中optimization 工具箱里的 fminimax函数求解最优值,经整理后螺杆结构参数优化数学模型为:
minFf(X)=F(η1D,η2θ,η3B,η4H),
(31)
X=(x1x2x3x4)T=(DθBH)T。
(32)
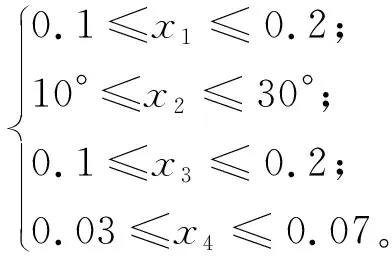
线性不等式约束:2x4-x1≤0。
非线性不等式约束:
x3-πtanθ(x1-x4)≤0;
综合分析螺旋外径、螺旋升角、轴向槽宽与径向齿高在优化目标中的变化趋势及范围,在统一数值量级的条件下运用层次分析法[14]在Matlab中经多次仿真计算,选定权重系数η1=0.75、η2=0.05、η3=1.00、η4=1.23。
4.4 优化计算及结果
利用Matlab对优化过程计算,经优化取整后得到螺杆的结构参数D、θ、B、H分别为153 mm,24.29°,141 mm,48 mm。优化后螺杆受到物料产生的摩擦力为0.975 2 N,比之前降低了51.38%。表1为优化前后结果对比。
5 螺杆受到物料摩擦力的ANSYS分析验证
根据优化后的参数对之前的螺杆三维有限元模型进行修改,然后分别将修改前后的有限元模型导入到Ansys Workbench中进行静力学分析,根据前述的螺杆受力分析模拟物料在螺杆槽内运动产生的摩擦力对螺杆造成的影响,对上述优化结果进行仿真验证。

表1 优化结果对比Table 1 The comparison results of optimization
图6为螺杆优化前后的等效应力云图。从图6中可看出,螺杆的表面应力由机头向固定端逐渐变大,螺纹上的应力是沿着螺旋线分布的,螺纹加载面上的应力值从螺纹根部向螺纹外缘逐渐增大,螺纹根部的应力值最大是由于弯矩及螺杆结构突变引起的应力集中。优化前后物料与螺杆之间由于摩擦产生的最大应力分别为6 368.7,2 039.6 MPa,优化后螺杆的应力有明显的下降,说明前述优化结果具有一定的可靠性。
图7为螺杆优化前后的变形云图。从图7中可看出,最大位移变形出现在受力端面,且从机头向固定端方向变形量逐渐减小。优化前后由于摩擦力对螺杆产生的最大变形值分别为21.928 0,8.197 6 mm,可看出优化后因摩擦产生的变形量对螺杆的影响有明显的改善,并不会因变形过大而导致与套筒内壁之间发生剧烈的摩擦和碰撞作用,致使螺杆与套筒的间隙过大不能正常挤出物料而报废,因此优化后的螺杆在机构运行过程中的使用性能更加趋于平稳。

图6 螺杆优化前后等效应力分析云图Figure 6 The equivalent stress analysis cloud chart before and after optimization of screw
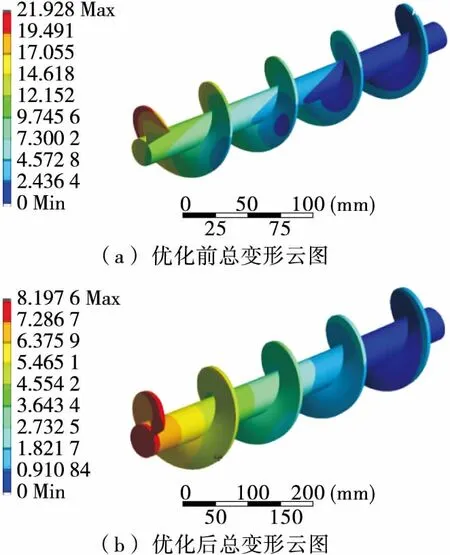
图7 螺杆优化前后总变形分析云图
图7 The total deformation analysis cloud chart before and after optimization of screw
综上,通过对优化前后的螺杆模型进行有限元仿真,得出该螺杆的模拟仿真结果基本能说明Matlab的数值优化结果的正确性,进一步表明所建立的螺杆受到物料摩擦阻力的力学模型的准确性。
6 结论
(1) 本研究基于连续介质假设原理,从螺杆结构参数角度建立单螺杆膨化机螺杆旋转挤压物料的摩擦阻力模型,得到摩擦阻力随螺杆的螺旋外径与螺旋升角的增大而减小,随着螺杆的轴向槽宽与径向齿高的减小而减小,且螺旋升角的变化对摩擦力的影响最为明显。
(2) 以螺杆受摩擦阻力为目标函数优化螺杆的各项结构参数,结果表明在满足膨化机生产效率的要求下优化后的摩擦阻力降低了51.38%。
(3) 对优化前后的螺杆进行有限元分析验证,结果表明优化后螺杆的应力与变形均有所改善,进一步表明所建力学模型的准确性。
通过优化分析计算出了单螺杆膨化机在物料加工过程中使螺杆受到物料的摩擦磨损最小时的最优结构参数,基于该方法可以在保证膨化机中主要零部件——螺杆的可靠性及寿命的前提下,提高膨化机的生产效率,改善产品的使用性能,为产品的优化、性能评价提供了一种全新的手段。
