山碴石填料路基沉降数值模拟研究

韩治勇， 方金苗， 李伟强

(1.皖西学院 建筑与土木工程学院， 安徽 六安 237012； 2.安吉城市投资集团有限公司， 浙江 安吉 313300)

0 引 言

山碴石作为山皮石中含石量较高的土石混合料，具有含石量高、石料强度大，并含有部分土质、砂粒等细集料，广泛存在于各类山体开采区[1].如能将储存量如此之大的山碴石填料运用于需求巨大的公路建设工程中，既能显著消耗山碴石储存量，缓解环境破坏的压力，又能替代常规的土质填料，从再生利用等绿色理念考虑，无疑会给公路建设带来极大的经济效益和社会效益.目前，国内外学者对山碴石类似土石混合料做了大量的研究，并取得了丰硕的成果[2-7].基于此，本研究拟在土石混合料的相关研究基础上，针对皖北地区山碴石填料的路用性能，从数值模拟角度对山碴石填料路基沉降进行分析，拟为类似公路工程建设提供参考.

1 山碴石路用性能数值模型

1.1 基本假定与模型建立

根据岩土体性质及其组成，利用Mohr-Coulomb破坏准则，本研究采用FLAC3D建立山碴石路基计算模型如图1所示.Mohr-Coulomb模型参数如表1所示.为了减少计算时间，取地基模型深度方向的厚度为6 m，模型的长×宽×高为12 m×5 m×6 m，地基模型共产生23 040个单元，29 350个节点；山碴石填筑路基模型按照松铺厚度为0.4 m，宽度5 m作为基础模型，共产生2 880个单元，3 675个节点.模型上部为自由面，侧面和底面均采用固定约束，其中侧面只约束水平方向的位移.由于路基的压实工艺采用动荷载振冲压实，对于土体的加固主要为动应力，而在土体中动应力的传播是以波的形式.为了精确地研究应力波在土体中的传播规律，网格的尺寸要求小于最小波长的1/10～1/8，计算模型的单元尺寸边长取为0.25 m以满足精度要求.

图1 地基计算模型示意图

1.2 边界条件

通常，初始地应力场的存在和影响不容忽略，它既是影响岩体力学性质的重要控制因素，也是岩体所处环境条件发生改变时引起变形和破坏的重要原因之一.同时，仿真模型的尺寸不可能无限大.因此，要想比较真实地进行工程模拟仿真，除了保证初始地应力场的可靠性外，还要选取合适的边界条件.初始地应力场生成的主要目的是为了模拟土体已存在的应力状态，而边界条件则是更好地实现仿真所必须.

本研究假定岩土体为均质、连续的各项同性体，则岩土体的自重应力场为，

σz=γ·H

(1)

(2)

式中，μ为泊松比；H为岩体至地表的距离，m；γ为上覆岩层容重，N/m3；σx、σy、σz分别为X、Y、Z方向的自重应力场，MPa.

因本计算模型考虑了足够的边界效应，故模型底面和四周均受链杆约束，顶面受荷载约束，即X轴边界限制X方向移动，Y轴边界限制Y方向的移动，Z轴(铅垂方向即深度方向)下边界限制Z方向移动，上边界地表为自由面.

2 数值模拟分析

2.1 振动碾压下路基应力场和位移场变化规律

鉴于试验段路基是在施工过程中一次填筑完成，且填筑高度为40 cm.故，本文后续数据分析时出现的h=0.4 m含义是，填筑路基的底面到山碴石路基表面的高度.同时，在仿真模拟强振碾压下路基应力场和位移场的变化规律时，只考虑在路基表面施加1次强振荷载(强振其冲击力取150 kN，其碾压速率为2，振动频率取30 Hz)来模拟路基振动碾压的过程，由于振动冲击的时间很短，不考虑冲击碾压后土体的固结，故只计算1次冲击作用下动力响应和位移的变化.在振动荷载作用下，山碴石填土路基在不同深度处的土体受1次冲击碾压时动应力的时程曲线如图2所示.

图2不同深度动应力时程曲线

由图2可以看出，土体单元动应力均出现2个应力波峰，第1波峰持续时间较长，为0.025 s，第二波峰持续时间较短.第二波峰主要是由在不同土层接触面之间波的反射造成， 当冲击波到达山碴石填土路基和地基的接触面时，会产生反射波.路基表面(h=0.4 m)在冲击碾压荷载作用下的最大峰值动应力为318 kPa，出现在0.014 s，而山碴石路基表面以下0.4 m(h=0 m)处的峰值动应力为56 kPa，出现在0.017 s，说明沿深度方向峰值动应力急剧减小.同时可见，通过冲击碾压的方式来加固山碴石路基，其冲击能量大部分作用于填土路基(填土高度为0.4 m).对于现场施工而言，由于填土地基经过静压处理，较为密实，而路基土体较为疏松，此时大部分冲击能被路基土体吸收，用来压缩固结.所以对于山碴石地基，后期碾压所导致的沉降主要为路基土体的压缩沉降量.

为研究冲击碾压的加固范围，根据土力学中对有效加固深度的规定，对于软土和一般土来说，附加应力分别取自重应力的10%和20%.由于粉黏土属于一般土，有效加固深度的临界值取为后者较大值(即取动应力和自重应力的比值为20%).动应力沿深度方向的变化曲线如图3所示.通常，动应力曲线与0.2倍自重应力线的交点即为加固范围的临界点，即冲击加固的有效深度约为3.8 m.

图3动应力沿深度变化曲线

从图3可以看出，动应力沿深度方向衰减很快且大致呈直线衰减，当冲击加载时间为0.01 s和0.02 s时，应力等值线有交叉点且都比0.015 s的应力值小，此和图2的变化规律一致.

不同深度处的土体经1次冲击碾压后的竖向位移时程曲线如图4所示.

图4不同深度下竖向位移时程曲线

从图4可以看出，山碴石路基在其表面处的沉降值最大，同时竖向位移随着时间的增加近似呈线性增加，竖向位移达到最大值后有较小的回弹，主要是因为山碴石填土路基一开始时呈较为松散的状态，此时的山碴石路基可以在极短的时间内被冲击压密.由于作用时间很短，土颗粒之间的力的传递滞后于冲击波的传递，所以当外部碾压结束之后，在数值模型中土体会继续有一定的沉降值.填土路基表面在1次冲击碾压荷载作用下的最终位移为3.2 cm，且在0.035 s时出现.由此可知，位移沿深度方向的传递规律和动应力相似，且随着深度的增加，土体位移出现峰值的时间相对滞后.

在振动碾压作用下，不同深度处的竖向位移沿径向变化的曲线如图5所示.

图5竖向位移沿径向分布曲线

从图5可以看出，不同深度处路基的竖向位移沿径向变化的规律基本相同.在振动碾压作用下，沉降与径向距离呈负相关，且衰减速率呈先快后缓，越靠近振动碾压的部位，沉降值越大.

2.2 山碴石填土路基沉降云图

本研究根据试验段的施工参数进行相应的碾压施工以及路基分层填筑，每层填筑的高度为40 cm.首先，采用自重25T的重型振动压路机稳压1遍，后弱振2遍、强振4遍，最后用18～21 T三轮压路机静压，直至压实合格后停止静压.碾压时由外侧向中间做进退式碾压，横向接头重叠宽度为1～2 m.本模型的动力荷载采用简化的正弦函数荷载，由于动荷载的作用时间很短，在模拟压实的过程中不考虑动力压实后的土体固结，只计算动力响应和位移变化.碾压时，压路机碾压速度控制在2～4 km/h之间，频率为20～30 Hz左右.

山碴石填土自重作用下的路基沉降云图如图6所示.

从图6中可以看出，其最大沉降值为1 mm，所以对于山碴石填土路基而言，其自重引起的路基沉降可以不计.

3 沉降影响因素分析

山碴石路基碾压完成的标准为路基表面外观无明显轮迹.故本研究填筑时结合水准仪沉降量检测压实效果，用振动压路机强振2遍碾压沉降量不大于2 mm.现场碾压中往往会出现个别路段最终的碾压沉降差大于2 mm，从而产生沉降不均匀的现象.

图6自重作用下路基沉降云图

3.1 填料分层厚度

为研究填料分层松铺碾压对路基压实效果的影响，在试验中，对于山碴石路基松铺选取3种分层方案：方案1，一次松铺60 cm；方案2，2层松铺，每次30 cm；方案3，3层松铺，每次20 cm.为保证每种方案总的碾压荷载相同，选取6遍静压，其中，方案2每松铺一层碾压3遍；方案3每松铺一层碾压2遍.

碾(静)压和6遍碾压之后路基的沉降云图如图7所示，不同填料分层厚度路基碾压累计沉降值如图8所示.

图7不同分层厚度路基压实沉降云图

结合图7与图8可以看出，方案1的山碴石路基采用一次松铺完成，在第3遍静压荷载压实之后，路基沉降增长值较小，其最终沉降量为7.5 cm.方案2采取2次松铺完成，每次松铺完成后，静压荷载进行3遍压实，共6遍碾压，其最终沉降量较方案1增加1.2 cm.方案3采用3次松铺完成，每次松铺完成后，静压荷载进行3遍压实，其最终沉降量较方案1增加1.9 cm.数据表明，山碴石路基分层碾压效果随分层数的增加越来越明显.

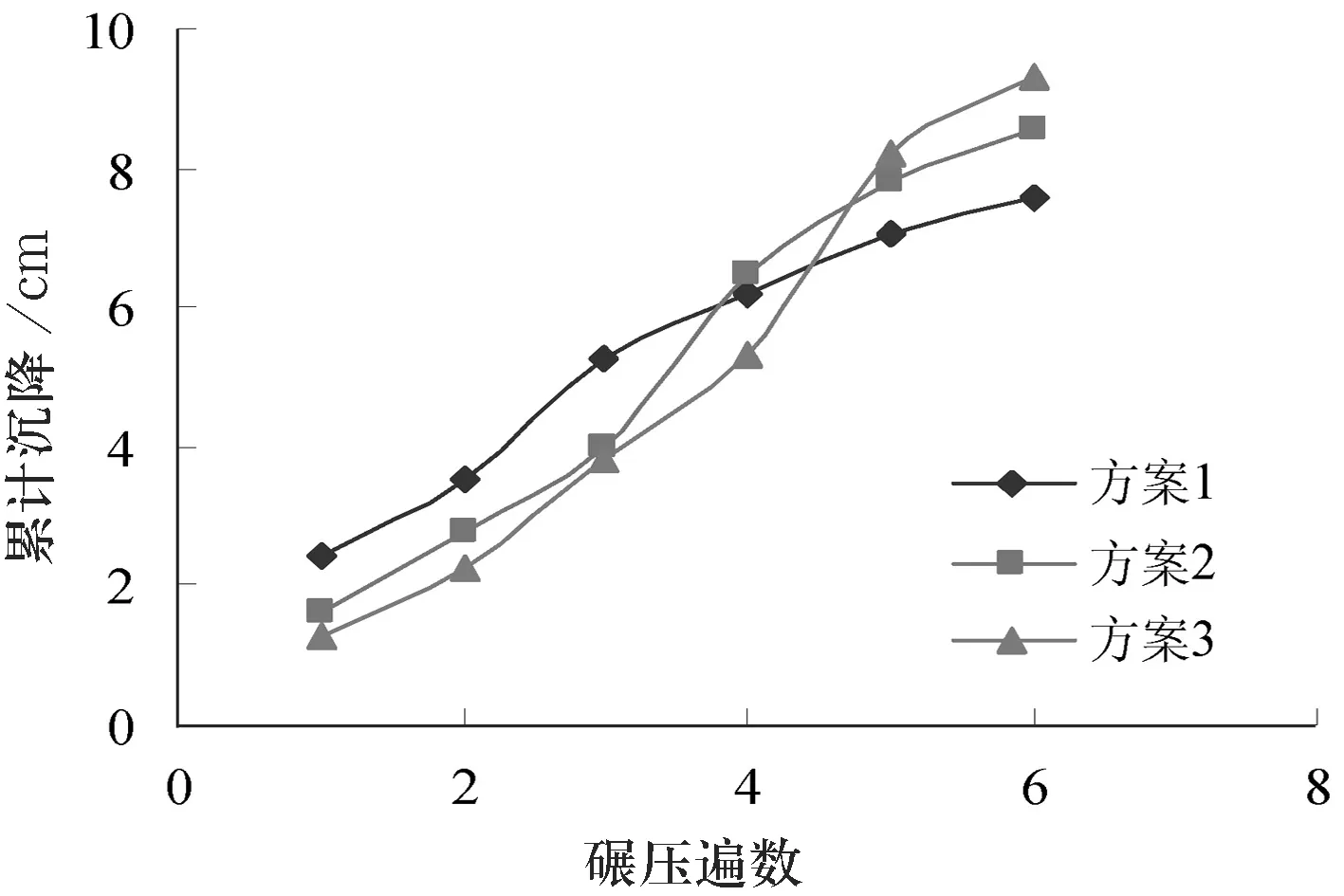
图8不同填料分层厚度路基碾压累计沉降值

3.2 山碴石填料参数

对于山碴石路基填筑工程来说，实际工程地质条件或者施工环节的影响会导致填筑时山碴石颗粒的不均匀，不同路段的山碴石路基填土的特性通常存在一定差异，在土体物理参数上则表现为路基土的粘聚力和弹性模量存在一定程度的差别，由于山碴石路基主要为颗粒状，粘聚力本身较小，这里就不做考虑.为研究其对山碴石路基不同路段的压实效果，有必要在仿真模型中改变土体的物理参数，对不同材料特性的山碴石碾压总沉降进行分析计算.不同弹性模量下，经过8次碾压作用下的位移沉降如图9所示.

图9不同弹性模量对路基竖向位移影响

由图9可知，弹性模量分别为30 MPa、40 MPa、50 MPa时，对应的最终沉降分别为8.2 cm、7.8 cm、7.4 cm.数据表明，随着土体弹性模量的增加，山碴石填土路基沉降量的下降幅度较大.弹性模量由30 MPa变化至50 MPa时，最大沉降量变化范围达到9.8%，可见，路基弹性模量对于山碴石填土路基沉降影响较大.因此，在实际路基施工过程中，应严格按照规范对路基填料的弹性模量等物理参数进行试验测定，以保证路基填筑压实的稳定.

4 结 论

在试验中，填土路基表面在一次冲击碾压荷载作用下的最终位移为3.2 cm，且在0.035 s时出现.位移沿深度方向的传递规律和动应力相似，且随着深度的增加，土体位移出现峰值的时间相对滞后.同时，试验中，山碴石路基采用一次松铺完成，在第3遍静压荷载压实之后，路基沉降增长值较小，其最终沉降量为7.5 cm；采取2次松铺完成，每次松铺完成后，静压荷载进行3遍压实，共6遍碾压，其最终沉降量为8.7 cm；采用3次松铺完成，每次松铺完成后，静压荷载进行3遍压实，其最终沉降量较方案1增加9.4 cm.说明山碴石路基分层碾压效果随分层数的增加越来越明显.当弹性模量分别为30 MPa、40 MPa、50 MPa时，对应的最终沉降分别为8.2 cm、7.8 cm、7.4 cm.说明随着土体弹性模量的增加，山碴石填土路基沉降量的下降幅度较大.弹性模量由30 MPa变化至50 MPa时，最大沉降量变化范围达到9.8%，可见路基弹性模量对于山碴石填土路基沉降影响较大.本研究表明，合理进行施工压实操作，对提高山碴石类似路基施工沉降具有重要的指导意义.