弧面分度凸轮机构压力角的通用表达式研究

李 俭， 饶 雄， 唐 茂， 邓女原媛， 熊美玲

(成都大学 机械工程学院， 四川 成都 610106)

0 引 言

目前，弧面分度凸轮被广泛应用于各种间歇运动机构中，其特点为刚度大、传动扭矩大、定位准确等.相关研究显示，间歇运动机构压力角是影响该类机构性能和受力情况的重要参数之一，其对机构的结构尺寸也有较大的影响.对此，国内外学者对弧面分度凸轮的廓面方程、机构压力角与主曲率等方面进行了研究，并取得了较多的成果[1-8].但在上述研究中，其推导过程比较复杂，且几何直观性不强.同时，由于滚子形状的不同以及凸轮轴与从动盘转动轴线之间角度的不同，从而造成最终数学表达式的不统一，这在一定程度上增加了公式推导的难度和工作量，致使在开发弧面凸轮相关软件时，相关工作变得极为繁琐与复杂[9-10].此外，目前尚未有相关文献报道过运用单参数曲面族包络面理论对弧面分度凸轮机构压力角通用表达式的研究.对此，本研究基于单参数曲面族包络面理论，将弧面分度凸轮滚子的不同形状(圆柱滚子、圆锥滚子及双曲线滚子)和凸轮轴与从动盘转动轴线之间形成不同角度时的情况进行统一性处理，推导出了弧面分度凸轮廓面方程的统一数学表达式，在此基础上建立了弧面分度凸轮机构压力角的通用表达式，并通过实际应用模型验证了本方法的正确性.

1 弧面分度凸轮廓面方程的建立

弧面分度凸轮机构示意图如图1所示，其相应的坐标系统及参数含义如图2、3所示.

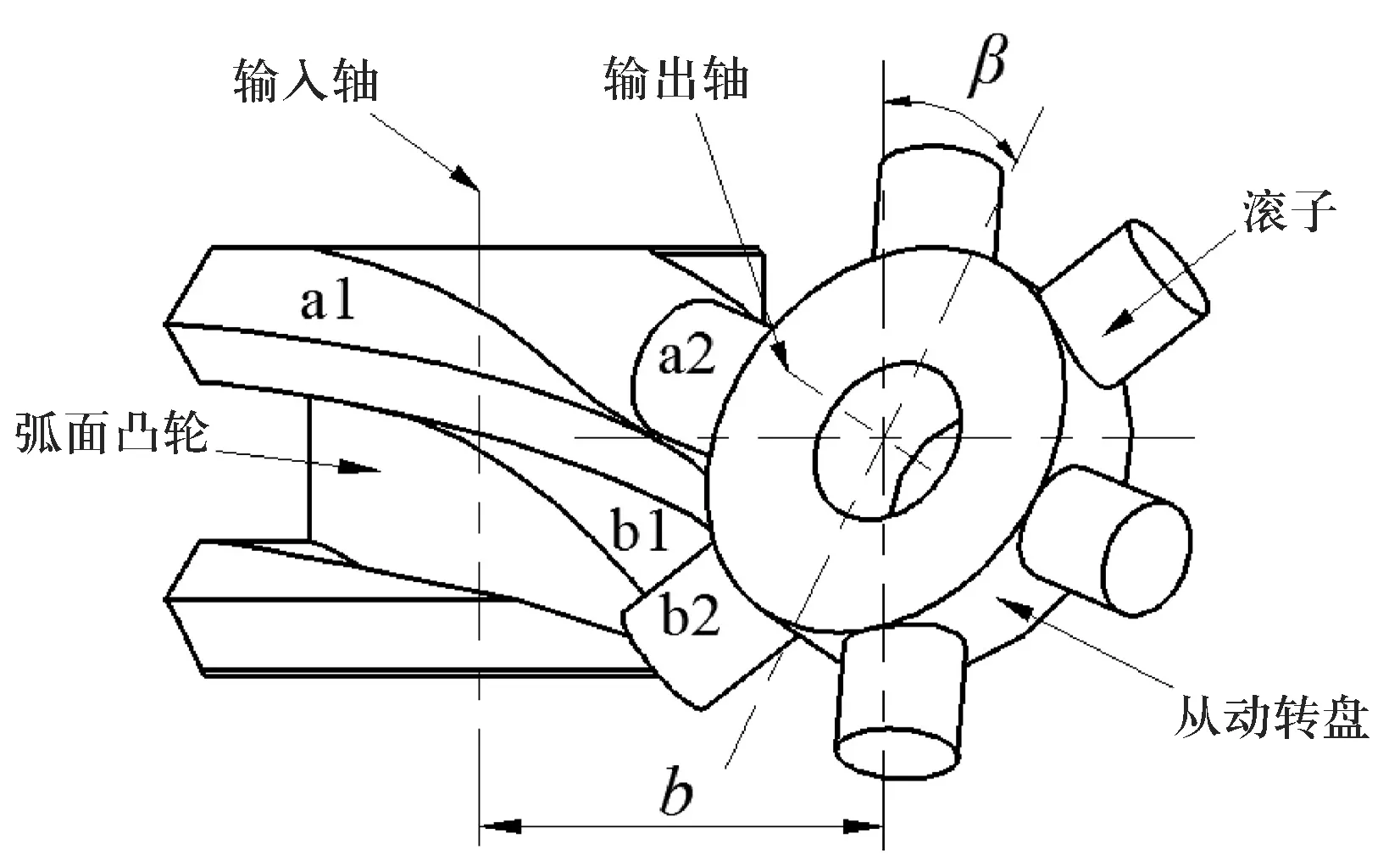
图1弧面分度凸轮机构简图

图2滚子示意图

图3滚子坐标系统

本研究基于单参数曲面族包络面理论[11-12]，将弧面分度凸轮的转动角位移φc视为该曲面族的参变量，同时也作为输入运动参数，从动转盘的转角位移φt作为输出运动参数.用滚子转角θ和沿滚子轴线的高度坐标h来描述滚子与弧面凸轮轮廓曲面相啮合的外表面曲面方程，再应用包络面理论建立弧面分度凸轮廓面方程的统一数学模型.预先给定运动规律，φt=φt(φc)，从而推导出弧面凸轮的轮廓曲面方程为，

rc=rc(θ，h,φc)={A1[cos(θ+β)sin(φt-α)cosφc-

cos(θ+β)sinβcos(φt-α)sinφc+sin(θ+β)×cosβsinφc]-A2[sin(θ+β)sin(φt-α)cosφc-sin(θ+β)sinβcos(φt-α)sinφc-cos(θ+β)×cosβsinφc]-(δ+L-h)[cos(φt-α)cosφc+sinβsin(φt-α)sinφc]+bcosφc}i-{A1[cos(θ+β)sin(φt-α)sinφc+cos(θ+β)sinβcos(φt-α)cosφc-sin(θ+β)cosβcosφc]-A2[sin(θ+β)sin(φt-α)sinφc+sin(θ+β)sinβcos(φt-α)cosφc+cos(θ+β)cosβcosφc]-(δ+L-h)×[cos(φt-α)sinφc-sinβsin(φt-α)cosφc]+bcosφc}j-{A1[cos(θ+β)cosβcos(φt-α)+sin(θ+β)sinβ]-A2[sin(θ+β)cosβcos(φt-α)-cos(θ+β)sinβ]+(δ+L-h)cosβsin(φt-α)k

(1)

式中，

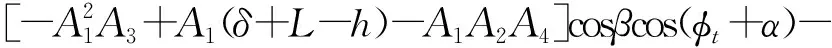
L-h)](φt′-sinβ)

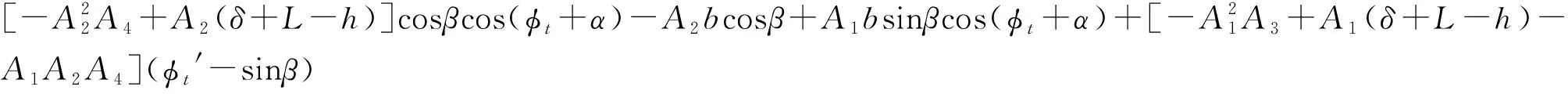
J=(A1A3+A2A4)sinβsin(φt+α)

A1=r+W1htanγ；A2=W2htanγ；

A3=W1tanγ；A4=W2tanγ.

其中：当W1=0，W2=0时，弧面凸轮的轮廓为圆柱滚子；当W1=1，W2=0时，弧面凸轮的轮廓为圆锥滚子；当W1=0，W2=1时，弧面凸轮的轮廓为双曲线滚子.

2 机构压力角的通用表达式

弧面凸轮机构压力角，是指弧面凸轮与滚子外表面共轭接触点处从动件运动方向与凸轮廓面法线之间的夹角，具体如图4所示.

图4弧面凸轮机构压力角示意图

设弧面凸轮与滚子在接触点处的单位公法矢量为n，该点处的压力角为Ψ，从动件的单位方向矢量为p，其中n由下式定义，

(2)

式中，

B1=[-sinβsinφccos(θ+β)A1+sinβsinφcsin(θ+β)A2-cosφc(A1A3+A2A4)]cos(-φt+α)+[-cosφcA1cos(θ+β)+cosφcA2sin(θ+β)+sinβsinφc(A1A3+A2A4)]sin(-φt+α)+cosβsinφc[cos(θ+β)A2+sin(θ+β)A1]

B2=[-sinβcosφccos(θ+β)A1+sinβcosφcsin(θ+β)A2+sinφc(A1A3+A2A4)]cos(-φt+α)+[-sinφcA1cos(θ+β)-sinφcA2sin(θ+β)+sinβcosφc(A1A3+A2A4)]sin(-φt+α)+cosβcosφc[cos(θ+β)A2+sin(θ+β)A1]

B3=-cosβ[cos(θ+β)A1-sin(θ+β)A2]cos(-φt+α)+cosβ(A1A3+A2A4)sin(-φt+α)-sinβ[cos(θ+β)A2+sin(θ+β)A1]

从动件运动的单位方向矢量p可由下式确定，

(3)

式中，Wt为从动件的速度矢量，在Ot—XtYtZt坐标系中，Wt在齐次坐标中用矩阵形式表示为，

Wt1=[0，0，ωt，1]T

(4)

经过坐标变换，可以推导出，

=ωt(-sinφccosβi-cosφccosβj+sinβk)

(5)

式中，ωt为从动件的转动角速度.

对于rM，如图4所示.

=bcosφci-bsinφcj+0k

(6)

故：

(7)

式中，

C1=-ωt{[-cosφcA1cos(θ+β)+cosφcA2sin(θ+β)+sinβsinφc(δ+L-h)]cos(-φt+α)+[sinβsinφccos(θ+β)A1-sinβsinφcsin(θ+β)A2+cosφc(δ+L-h)]sin(-φt+α)}

C2=-ωt{[-sinφcA1cos(θ+β)-sinφcA2sin(θ+β)+sinβcosφc(δ+L-h)]cos(-φt+α)-[-sinβcosφccos(θ+β)A1+sinβsinφcsin(θ+β)A2+sinφc(δ+L-h)]sin(-φt+α)}

C3=-ωtcosβ{cos(-φt+α)(δ+L-h)+sin(-φt+α)[cos(θ+β)A1-sin(θ+β)A2]}

至此，弧面凸轮机构压力角的通用表达式为，

(8)

由(8)式可见，弧面分度凸轮压力角是从动件运动规律与弧面凸轮机构几何尺寸的复杂函数，故在机构设计时可通过改进从动件运动规律或弧面凸轮几何尺寸等方式来调整压力角的大小.

3 模型验证

为验证弧面凸轮机构压力角数学模型的正确性，本研究通过数值模拟工具Mathematica对该模型进行了验证.所取弧面分度凸轮机构的机构参数如下：r=12.05 mm，L=15 mm，b=70 mm，α=30 °，δ=31 mm，β=0 °，γ=0 °.滚子数z=6；在整个运动周期中，分度期τ=270 °，休止期φd=90 °；从动转盘的运动规律为改进型正弦曲线运动关系，具体如公式(9)、(10)、(11)所示.

(9)

(10)

(11)

将上述参数代入计算模型后获得的弧面凸轮机构压力角沿接触线的分布情况如图5所示(仅列出了受力面).数值计算结果验证了本研究提出的弧面凸轮机构压力角数学模型的正确性.

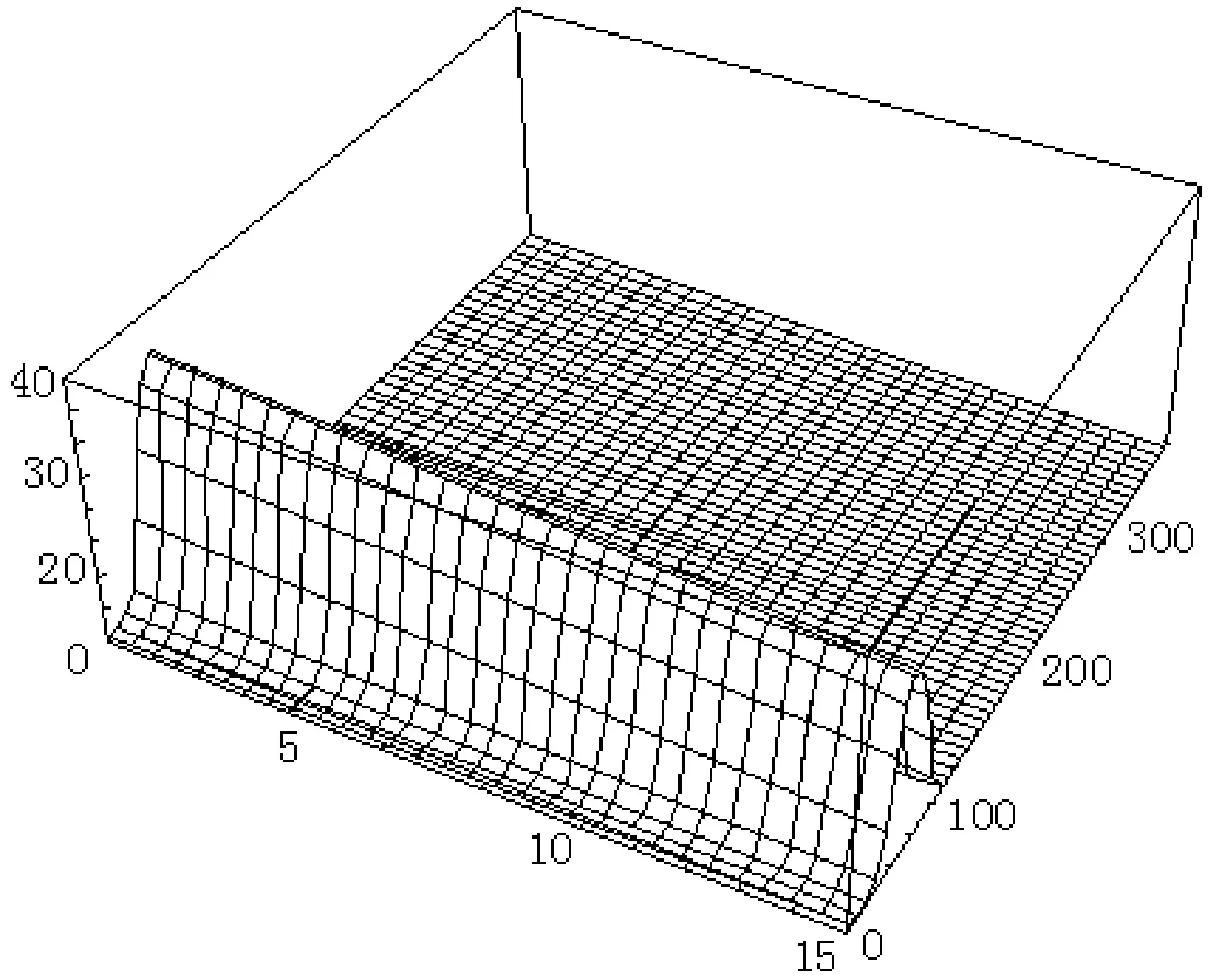
图5弧面分度凸轮受力面机构压力角沿接触线的分布情况

4 结 论

本研究以包络面理论为依据，运用齐次坐标的矩阵变换，建立了统一数学模型的弧面分度凸轮轮廓曲面方程，并推导出了该机构压力角的通用表达式.推导过程所使用的方法几何直观性强，整个过程简单明了，表达形式统一且便于理解，并且不需进行复杂的运动分析.弧面凸轮机构压力角的数学模型的统一表达，有助于验证弧面凸轮设计参数与运动规律的正确性.同时，也对弧面分度凸轮机构的数字化设计与制造具有一定的实用价值，为开发相应软件提供了理论依据.