初中物理“人眼视物”问题的讨论*
2018-10-10汪小玲林钦
汪小玲 林钦
(福建师范大学物理与能源学院 福建 福州 350117)
初中物理在凸透镜成像规律学习时往往都会涉及人眼视物问题,包括眼睛的成像规律、视力参数“远点”等.现行的各版本教材因篇幅等条件的限制,往往没有把内容介绍清楚,物理教师受课时等条件的制约,一般不会做过多的扩展.例如, 教材将“远点”定义为“依靠眼睛调节能看清的最远的极限点”,并指明正常人眼的远点在无穷远[1].这导致不少学生存在困惑:既然人眼能看清的最远点在无穷远,为什么人不能看到无穷远的物体呢?
溯本求源方知其精髓.因此,有必要针对“人眼视物”问题进行详细讨论,为物理教师的教学提供参考.
在“人眼视物”这个问题上,关键在于怎么“看到”.人类之所以能够看到客观世界,是因为眼睛接收到了来自客观物体发射、反射或散射的光[2].因此,我们对“人眼视物”的分析应该从人眼的工作原理出发,主要讨论两个问题:(1)人眼的成像系统;(2)人眼的分辨率.
1 人眼的成像系统
从光学角度来说,眼睛属于一种光学成像仪器,其成像特点可以简化为球面折射进行讨论.对于中学生来说,眼睛成像更加类似于凸透镜成像.如图1所示,眼睛的晶状体和角膜的共同作用犹如一个凸透镜,光线经晶状体的作用会聚在视网膜上形成像,经视神经作用输入大脑.需要注意的是,人眼睫状肌的伸缩可以改变晶状体的曲率半径,因而可以使不同距离的物体清晰地在视网膜上成像,此时晶状体与视网膜之间的距离就是像距.也就是说,人眼结构可以简化为一个凸透镜和光屏,且这个凸透镜在一定范围内可以根据需要而自动调节焦距[1].
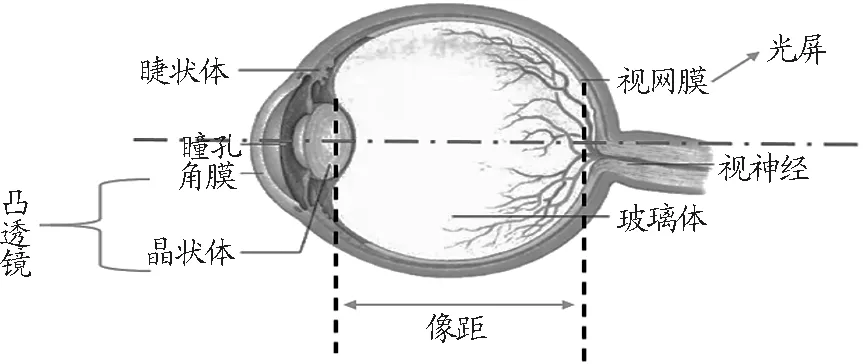
图1 眼睛结构
在人眼的光学系统中,正常的调节可以改变晶状体的焦距,所以眼睛可以看清距离不同的物体.事实上,晶状体的曲率半径达到最大值时,焦距最长,此时在视网膜上可以清晰成像的物体到人眼的距离就是远点[2].超出远点的物体,经晶状体后所成的像距小,在未到达视网膜的位置聚合,则视网膜只能接收到模糊的像,故对于远点外的物体无法辨别细节.
初中教材中所指“正常人眼的远点在无穷远”指的是医学上的“正视眼”,在睫状肌完全放松情况下,远处物体在视网膜清晰成像.眼睛的调节能力由睫状肌的收缩功能决定,随着年龄的增长,肌肉收缩功能衰退,加上眼睛结构上可能出现其他缺陷,如晶状体位置不正等,所以在现实人群中出现“正视眼”的概率很小[3].事实上,人眼除了“正视眼”之外,大多数人的眼睛属于“近视眼”或者“远视眼”的范围.晶状体的形状发生变化,对于光线的作用发生改变,此时就不再是理想成像,视网膜上就接收不到清晰的像.如图2所示,晶状体正常情况下,光线在视网膜上会聚,成像清晰,即正视眼;当晶状体形状变厚,经晶状体作用的光线在视网膜前会聚,导致视网膜上的像模糊,这就是近视眼;当晶状体形状变薄,经晶状体作用的光线在视网膜后才会聚,视网膜上也无法接收到清晰的像,这就是远视眼.所以当眼睛出现近视或者远视时,需要配戴一定透镜制作的眼镜加以矫正.
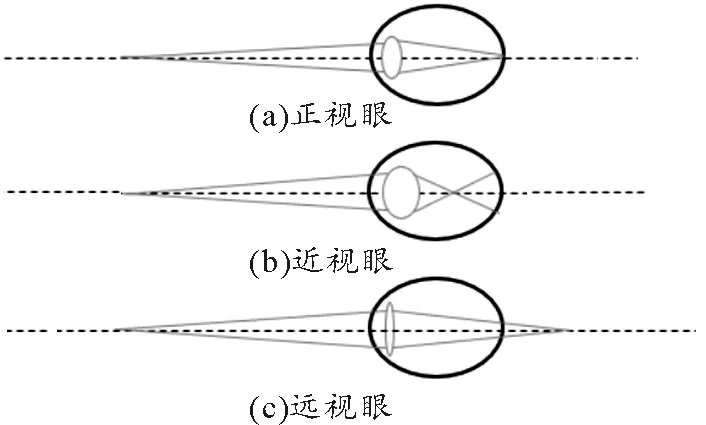
图2 正视、近视和远视
2 人眼的分辨率
在上面的讨论中,我们其实忽视了一个问题:光线是从哪里进入到晶状体的.其实人眼视物的光线是从瞳孔进来的,瞳孔在人眼系统中起到一个非常关键的作用.物理光学中,任何一个物体经一定大小的光学孔径成像后,都会发生衍射,在几何像点的位置上,就会产生一个艾里斑[2].如图3所示,空间位置不同的物体沿不同角度投射的光线进入孔径(瞳孔),会形成不同的艾里斑,当两个艾里斑的空间距离很近时,就会发生重叠,导致无法分辨.对于既定的光学成像系统,在一定大小的孔径发生衍射现象后,分辨本领满足瑞利公式
式中λ为可见光的波长,d为小孔直径,Δθ0为艾里斑的半角宽度.由瑞利公式可知,光学元件的孔径d越大时,最小张角越小,即可分辨的间隔越小,分辨率越大.
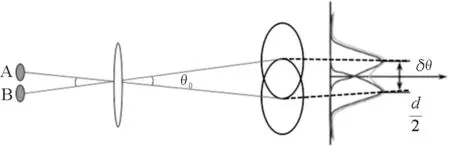
图3 瑞利判据:最小分辨角
在人眼结构中,人眼的瞳孔相当于一个直径大小在一定范围内可变的孔径光阑,光线进入瞳孔后将发生衍射.人的瞳孔大小有限,约2.5~4 mm[4],这样人眼的光学系统就存在一个分辨极限.若某人瞳孔为极限直径4 mm,对于550 nm的色光而言,此时的极限分辨角为0.6′,但瞳孔直径过大时,眼睛像差产生影响,分辨角反而增大.所以一般认为人眼的极限分辨角为1′,即θmin=1′=2.908×10-4rad[5].
基于人眼的成像系统,曾有一个有意思的争论——在太空上人眼能否看到长城.这个问题的产生要追溯到人类对于宇宙的探索,前苏联宇航员根纳季·斯特列卡洛和美国宇航员尤金·塞尔南在公开场合表示在太空上人眼可以看到长城,2000年凤凰卫视采访宇航员奥尔德林,他表示在太空无法看到长城.2004年5月11日欧洲空间局在首页网站发布一张高分辨率卫星图像,并配文指出从太空看到了长城,神州五号的宇航员杨利伟返回地球时明确表示在太空无法看到长城[6].在这种矛盾的冲击下,不管是学术界还是民间都有很多论证,讨论分析的结果也不尽相同.
从物理学角度来说,这是一个属于人眼光学成像范畴的问题,通常情况下,我们可以根据上面的分析进行简单计算.取人眼瞳孔的最大直径4 mm,可见光的波长范围为400~760 nm(取人眼敏感的绿光波长550 nm),长城宽度最大的城台处大约有6 m[7].在天气条件理想的情况下,我们可以用瑞利判据进行计算
λ=550 nm=5.5×10-7m
d=4 mm=4.0×10-3m
最小分辨角
想看到6 m宽的长城,极限距离如图4所示,应该为
3.576 8×104m=35.768 km
若采用公认的人眼的极限分辨角1′,则此时的极限距离仅有20.633 km.
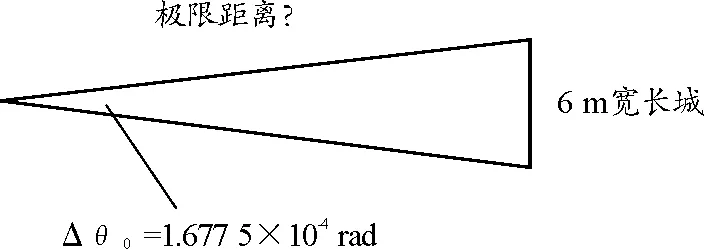
图4 眼睛视物的极限距离
显然,这样的极限距离远低于公认的太空高度,也就是说在遥远的太空,人眼是无法分辨出长城的.事实上,就“太空上能否看到长城?”的争议,从事遥感应用研究的戴昌达教授在早些年做了十分严谨的探索,戴老师在理论分析的基础上进行了空间遥感实验,对争议中出现的各种反对意见一一做出反驳,最后得出在太空人眼不能看到长城的结论[7].
