匀速圆周运动的相对运动演示软件设计*
2018-10-10王超陈攀杰周艳丽
王超 陈攀杰 周艳丽
(台州学院物理系 浙江 台州 318000)
1 引言
圆周运动是中学物理以及大学物理力学部分中一种重要的曲线运动,其在现实生活中非常常见,如轮子绕轴的转动、圆锥摆的运动、卫星绕地球的转动等.通常我们只讨论一个物体的圆周运动[1~5],但有时会遇到两个都做圆周运动的物体的相对运动问题,如:地球表面的人观察地球卫星的运动(人和卫星都绕地心做圆周运动),或者太阳系中其他行星相对地球的运动(地球和其他行星都近似绕太阳做圆周运动),地球卫星间的相对运动等[6].相对运动问题是力学部分的难点,其往往与坐标系的选取有关.以xOy平面内做圆周运动的A,B两质点为例,当我们讨论B相对于A的运动时,需要以A为原点建立二维直角坐标系(x′Ay′)并在该坐标系中讨论B的运动.坐标系x′Ay′随A点一起运动,若x′轴和y′轴始终分别与基坐标系的x轴和y轴平行,则称x′Ay′系为平动坐标系;若x′轴和y′轴绕A点转动,则称x′Ay′系为转动坐标系[7].在不同的坐标系中,B相对于A的运动轨迹往往不同.例如:我们在地球表面观察赤道上空地球同步卫星的运动,在转动坐标系中,卫星相对于我们静止,而在平动坐标系中卫星则相对于我们不停地运动.
本文基于Visual Basic语言开发出用于演示二维平面内两个做匀速圆周运动的质点的相对运动轨迹的仿真软件,利用该软件可以直观演示任意参数条件下做匀速圆周运动两质点在平动坐标系和转动坐标系中的相对运动轨迹.
2 理论模型
假定两个质点1和2在基坐标系xOy平面内各自沿逆时针做匀速圆周运动,圆心坐标分别为(x01,y01)和(x02,y02),半径分别为R1和R2,角速度分别为ω1和ω2,t= 0时刻两质点到圆心的连线与Ox轴的夹角分别为α1和α2,则任意t时刻两个质点在xOy平面内的坐标可表示为
(1)
(2)
若以质点1为坐标原点建立平动坐标系x1O1y1,如图1(a)所示,则质点2相对于质点1的坐标可表示为
(3)
同理,以质点2为坐标原点建立平动坐标系x2O2y2,如图1(a)所示,则质点1相对于质点2的坐标可表示为
(4)
对比式(3)和式(4)不难得到
(5)

(6)

(7)

图1 平动坐标系和转动坐标系示意图
当ω1=ω2时,即ω1∶ω2= 1∶1,根据上述公式可以证明:无论是在平动坐标系或是在转动坐标系,两个质点的相对运动轨迹都为圆(圆周半径R的大小与x01,y01,x02,y02,R1,R2,α1和α2有关,而且在某些特殊条件下R= 0,即质点相对静止).考虑到推导过程和最终表达式非常繁琐,这里不再列出.当ω1≠ω2时,两个质点的相对运动轨迹很难通过直接推导进行表达.本文基于VB语言根据式(1)~(7)求出任意t时刻两个质点在基坐标系中的坐标以及在平动坐标系和转动坐标系中的相对坐标,继而绘制并得到两个质点的相对运动轨迹.
3 基于VB语言的演示软件设计
软件程序分窗体和模块两部分.软件将各种操作集中在一个窗体内,其中包含参数设置、命令按钮和图形输出3个部分,如图2所示.参数设置部分包含两个质点在基坐标系中的圆心位置、圆周半径、角速度、初始角度、计算时间间隔dt和计算次数Num等参数;命令按钮部分包含系统生成、开始运动和结束程序3个按钮;图形输出部分包含基坐标系中两个质点的运动轨迹、平动坐标系和转动坐标系中两个质点的相对运动轨迹等5个区域.软件程序的执行按照一定的流程进行设计,即首先进行参数设置并点击系统生成按钮,程序在“基坐标系中两个质点的运动轨迹”区域绘制两个质点的圆轨迹及初始位置;然后点击开始运动按钮,程序将从t= 0时刻开始每间隔dt根据式(1)~(7)计算两个质点的位置,连续计算Num次,且每次计算都在图形区域同步绘制质点位置代表点,从而获得基坐标系中两个质点的运动图像以及两个质点间的相对运动的动态轨迹;最后点击结束程序,终止程序并关闭软件,具体流程图如图3所示(程序代码详见附录).
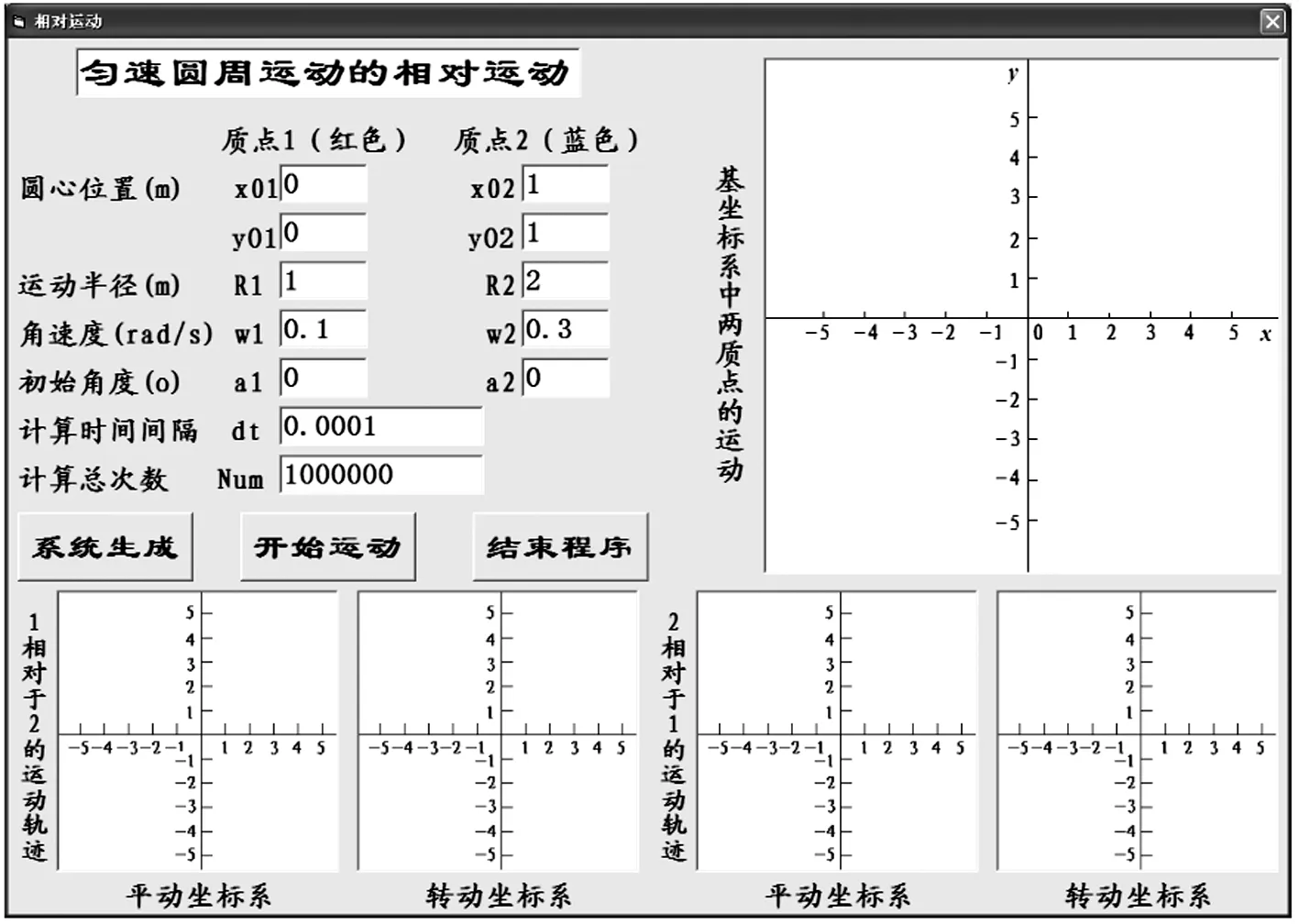
图2 窗体界面
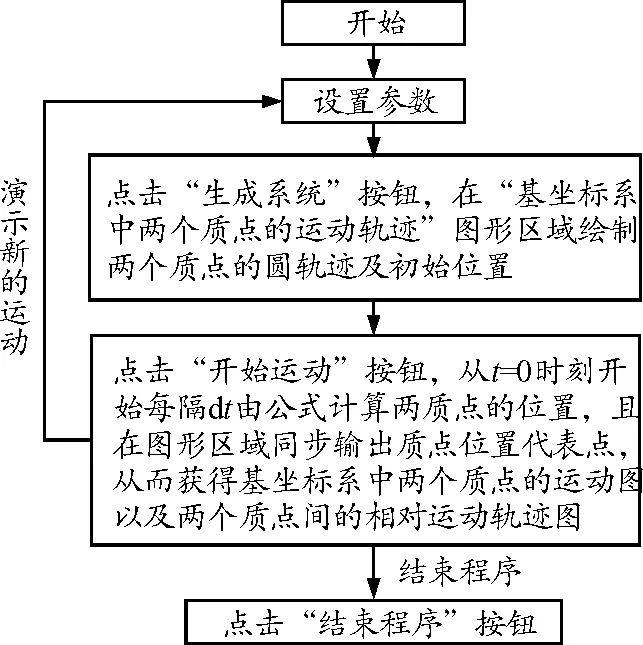
图3 程序流程图
4 演示结果举例
作为例子,我们设定:质点1的圆心位置(0, 0),半径为1.0,初始角度为0;质点2的圆心位置(0, 0),半径为2,初始角度为0,即两个质点做同心转动.我们发现质点的相对运动轨迹形状仅与两个质点圆周运动角速度比值有关而与角速度具体值无关.表1给出了角速度比值ω1∶ω2分别为1∶1,1∶2和1∶3时两质点在平动坐标系和转动坐标系中的相对运动轨迹图及其对应的轨迹方程.由图可以看出,当ω1∶ω2= 1∶1时,相对运动轨迹图形和方程都比较简单,而当ω1∶ω2≠ 1∶1时,相对运动轨迹图形和方程都会随ω1∶ω2的减小(或增大)变得越来越复杂.通常情况下,转动坐标系中两个质点的相对运动轨迹形状或大小不相同,而平动坐标系中两个质点的相对运动轨迹大小相同且形状相似,这一特点可由式(5)直接得出.
表1质点相对运动轨迹演示结果图例

5 结论
圆周运动是物理力学部分常见的曲线运动.本文基于VB语言开发出用于演示二维平面内做匀速圆周运动两质点的相对运动轨迹的仿真软件.在任意给定参数条件下,利用该软件可分别绘出平动坐标系和转动坐标系中质点的相对运动轨迹,从而形象直观展现做匀速圆周运动两质点的相对运动规律.该软件可用于教师课堂演示或学生课外自主演示,拓展圆周运动和相对运动知识,使物理知识化抽象为形象生动,提高学生学习兴趣和参与性.
附录:VB程序代码
Const unitlen1 = 500, unitlen2 = 300, boxxmax = 200, boxymax = 200, ntimemax = 1000000
Dim ntimereal As Long, ntime As Long, pdeltt As Long
Dim deltt As Double, pai As Double, i As Double, x01 As Double, y01 As Double, x02 As Double, y02 As Double, r1 As Double, r2 As Double, w1 As Double, w2 As Double, a1 As Double, a2 As Double, x1 As Double, x2 As Double, x12 As Double, x21 As Double, y1 As Double, y2 As Double, y12 As Double, y21 As Double, sx1 As Double, sx2 As Double, sx12 As Double, sx21 As Double, sy1 As Double, sy2 As Double, sy12 As Double, sy21 As Double, rx12 As Double, rx21 As Double, ry12 As Double, ry21 As Double, srx12 As Double, srx21 As Double, sry12 As Double, sry21 As Double, centerx1 As Double, centery1 As Double, centerx2 As Double, centery2 As Double, centerx3 As Double, centery3 As Double, centerx4 As Double, centery4 As Double, centerx5 As Double, centery5 As Double, deltt2 As Double, rtime As Double
'生成系统
Private Sub Command1_Click()
pai = 3.1415926
x01 = Val(Text1.Text)
y01 = Val(Text2.Text)
x02 = Val(Text3.Text)
y02 = Val(Text4.Text)
r1 = Val(Text5.Text)
r2 = Val(Text6.Text)
w1 = Val(Text7.Text)
w2 = Val(Text8.Text)
deltt = Val(Text9.Text)
ntimereal = Val(Text10.Text)
pdeltt = 100
a1 = Val(Text12.Text) * pai / 180
a2 = Val(Text13.Text) * pai / 180
deltt2 = deltt * deltt
centerx1 = Val(Picture1.Width) / 2
centery1 = Val(Picture1.Height) / 2
centerx2 = Val(Picture2.Width) / 2
centery2 = Val(Picture2.Height) / 2
centerx3 = Val(Picture3.Width) / 2
centery3 = Val(Picture3.Height) / 2
>centerx4 = Val(Picture4.Width) / 2
centery4 = Val(Picture4.Height) / 2
centerx5 = Val(Picture5.Width) / 2
centery5 = Val(Picture5.Height) / 2
x1 = x01 + r1 * Cos(a1)
y1 = y01 + r1 * Sin(a1)
x2 = x02 + r2 * Cos(a2)
y2 = y02 + r2 * Sin(a2)
x12 = x1 - x2
y12 = y1 - y2
x21 = -x12
y21 = -y12
rx12 = x12
ry12 = y12
rx21 = x21
ry21 = y21
sx01 = centerx1 + x01 * unitlen1
sy01 = centery1 - y01 * unitlen1
sx1 = centerx1 + x1 * unitlen1
sy1 = centery1 - y1 * unitlen1
sx02 = centerx1 + x02 * unitlen1
sy02 = centery1 - y02 * unitlen1
sx2 = centerx1 + x2 * unitlen1
sy2 = centery1 - y2 * unitlen1
sx12 = centerx2 + x12 * unitlen2
sy12 = centery2 - y12 * unitlen2
sx21 = centerx3 + x21 * unitlen2
sy21 = centery3 - y21 * unitlen2
srx12 = centerx4 + rx12 * unitlen2
sry12 = centery4 - ry12 * unitlen2
srx21 = centerx5 + rx21 * unitlen2
sry21 = centery5 - ry21 * unitlen2
Picture1.Cls
Picture2.Cls
Picture3.Cls
Picture4.Cls
Picture5.Cls
Picture1.FillColor = vbBlack
Picture1.FillStyle = 0
Picture1.Circle (sx01, sy01), 25, vbBlack
Picture1.FillColor = vbRed
Picture1.FillStyle = 1
Picture1.Circle (sx01, sy01), r1 * unitlen1, vbRed
Picture1.FillStyle = 0
Picture1.Circle (sx1, sy1), 100, vbRed
Picture1.FillColor = vbBlack
Picture1.FillStyle = 0
Picture1.Circle (sx02, sy02), 25, vbBlack
Picture1.FillColor = vbBlue
Picture1.FillStyle = 1
Picture1.Circle (sx02, sy02), r2 * unitlen1, vbBlue
Picture1.FillStyle = 0
Picture1.Circle (sx2, sy2), 100, vbBlue
Picture2.FillColor = vbRed
Picture2.FillStyle = 0
Picture2.Circle (sx12, sy12), 25, vbRed
Picture3.FillColor = vbBlue
Picture3.FillStyle = 0
Picture3.Circle (sx21, sy21), 25, vbBlue
Picture4.FillColor = vbRed
Picture4.FillStyle = 0
Picture4.Circle (srx12, sry12), 25, vbRed
Picture5.FillColor = vbBlue
Picture5.FillStyle = 0
Picture5.Circle (srx21, sry21), 25, vbBlue
End Sub
'开始运动
Private Sub Command2_Click()
rtime = 0#
For ntime = 1 To ntimereal
rtime = rtime + deltt
x1 = x01 + r1 * Cos(w1 * rtime + a1)
y1 = y01 + r1 * Sin(w1 * rtime + a1)
x2 = x02 + r2 * Cos(w2 * rtime + a2)
y2 = y02 + r2 * Sin(w2 * rtime + a2)
x12 = x1 - x2
y12 = y1 - y2
rx12 = x12 * Cos(w2 * rtime) + y12 * Sin(w2 * rtime)
ry12 = -x12 * Sin(w2 * rtime) + y12 * Cos(w2 * rtime)
x21 = -x12
y21 = -y12
rx21 = x21 * Cos(w1 * rtime) + y21 * Sin(w1 * rtime)
ry21 = -x21 * Sin(w1 * rtime) + y21 * Cos(w1 * rtime)
If ntime Mod pdeltt = 0 Then
sx01 = centerx1 + x01 * unitlen1
sy01 = centery1 - y01 * unitlen1
sx1 = centerx1 + x1 * unitlen1
sy1 = centery1 - y1 * unitlen1
sx02 = centerx1 + x02 * unitlen1
sy02 = centery1 - y02 * unitlen1
sx2 = centerx1 + x2 * unitlen1
sy2 = centery1 - y2 * unitlen1
sx12 = centerx2 + x12 * unitlen2
sy12 = centery2 - y12 * unitlen2
sx21 = centerx3 + x21 * unitlen2
sy21 = centery3 - y21 * unitlen2
srx12 = centerx4 + rx12 * unitlen2
sry12 = centery4 - ry12 * unitlen2
srx21 = centerx5 + rx21 * unitlen2
sry21 = centery5 - ry21 * unitlen2
If ntime Mod 10000 = 0 Then
Picture1.Cls
Picture1.FillColor = vbBlack
Picture1.FillStyle = 0
Picture1.Circle (sx01, sy01), 25, vbBlack
Picture1.FillColor = vbRed
Picture1.FillStyle = 1
Picture1.Circle (sx01, sy01), r1 * unitlen1, vbRed
Picture1.FillStyle = 0
Picture1.Circle (sx1, sy1), 100, vbRed
Picture1.FillColor = vbBlack
Picture1.FillStyle = 0
Picture1.Circle (sx02, sy02), 25, vbBlack
Picture1.FillColor = vbBlue
Picture1.FillStyle = 1
Picture1.Circle (sx02, sy02), r2 * unitlen1, vbBlue
Picture1.FillStyle = 0
Picture1.Circle (sx2, sy2), 100, vbBlue
End If
Picture2.FillColor = vbRed
Picture2.FillStyle = 0
Picture2.Circle (sx12, sy12), 25, vbRed
Picture3.FillColor = vbBlue
Picture3.FillStyle = 0
Picture3.Circle (sx21, sy21), 25, vbBlue
Picture4.FillColor = vbRed
Picture4.FillStyle = 0
Picture4.Circle (srx12, sry12), 25, vbRed
Picture5.FillColor = vbBlue
Picture5.FillStyle = 0
Picture5.Circle (srx21, sry21), 25, vbBlue
End If
Next ntime
End Sub
'结束程序
Private Sub Command3_Click()
End
End Sub
