轨迹圆与磁场圆等大时带电粒子运动模型分析
2018-10-10陈玺君
陈玺君
(丹阳市吕叔湘中学 江苏 镇江 212300; 广西师范大学物理科学与技术学院 广西 桂林 541004)
1 引言
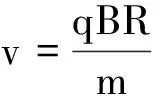
2 问题场景
在磁场教学中教师经常让学生解决这样一个问题:
【典例】如图1(a)所示,x轴正方向水平向右,y轴正方向竖直向上.在xOy平面内有与y轴平行的匀强电场,在半径为R的圆形区域内加有与xOy平面垂直的匀强磁场.在坐标原点O处放置一带电微粒发射装置,它可以连续不断地发射具有相同质量m,电荷量q(q>0)和初速度为v0的带电粒子.已知重力加速度大小为g.
(1)当带电微粒发射装置连续不断地沿y轴正方向发射这种带电微粒时,这些带电微粒将沿圆形磁场区域的水平直径方向离开磁场,并继续沿x轴正方向运动.求电场强度和磁感应强度的大小和方向.
(2)调节坐标原点O处的带电微粒发射装置,使其在xOy平面内不断地以相同速率v0沿不同方向将这种带电微粒射入第Ⅰ象限,如图1(b)所示.现要求这些带电微粒最终都能平行于x轴正方向运动,则在保证匀强电场、匀强磁场的强度及方向不变的条件下,应如何改变匀强磁场的分布区域?并求出符合条件的磁场区域的最小面积.
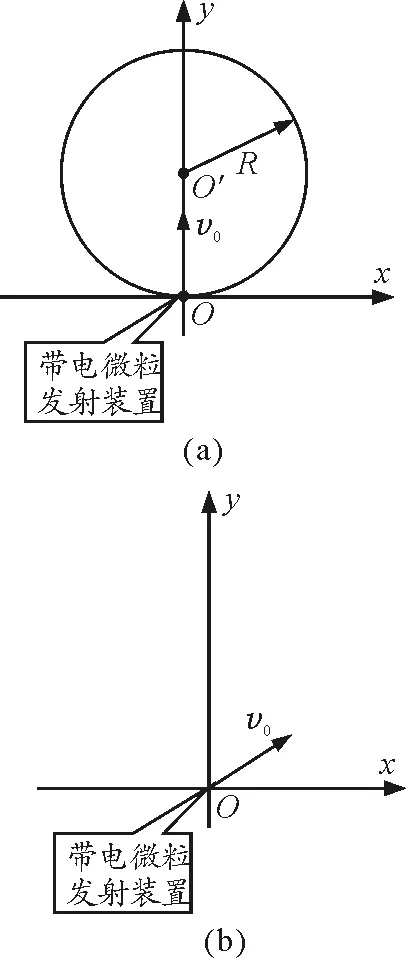
图1 题图
笔者发现,在教学过程中,对于典例中第(2)问的求解过程,学生感觉难度很大,如果在解决该问题之前,能够先熟悉掌握以下运动模型,可以使教学变得从容,从而让学生求解以上问题变得更加轻松.
3 模型概述
设圆形磁场方向垂直纸面向外,磁感应强度大小为B,一带正电的微粒从圆形磁场圆形边界A点入射.为方便讨论,本文中带电粒子的速率v不做特别说明均认为
其中q为带电粒子的电荷量,B为圆形匀强磁场的磁感应强度,R为带电粒子在匀强磁场中的圆轨迹半径,亦为磁场圆的半径,m为带电粒子的质量,粒子的重力不计.
4 模型结论
结论1:带电粒子以速率v从圆形匀强磁场边界任意位置沿半径射入磁场,必沿半径方向射出磁场.
证明:如图2所示,AO=BO=AO′=BO′,且AO⊥AO′,BO′⊥BO,故四边形AOBO′为正方形,BO⊥BO′,因此vB与BO在一条直线上,沿半径方向射出磁场.
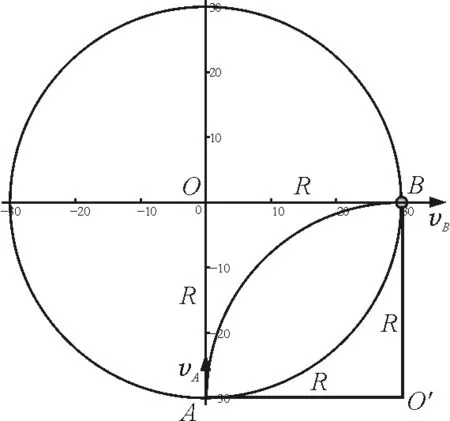
图2 结论1分析图
结论2:带电粒子以速率v从圆形匀强磁场边界任意位置以任意方向进入磁场,则粒子出磁场时的速度方向必垂直于粒子进磁场位置所在的圆直径且平行于入射点磁场圆的切线.
证明:如图3所示,过A点作直线AC与磁场圆相切,过B点作vB的反向延长线BD,O和O′为磁场圆与轨迹圆的圆心,AO=BO=BO′=AO′=R,故四边形AOBO′为菱形,BD⊥AO,vB⊥AO,即vB⊥AE(直径),而AC⊥AO,vB∥AC.
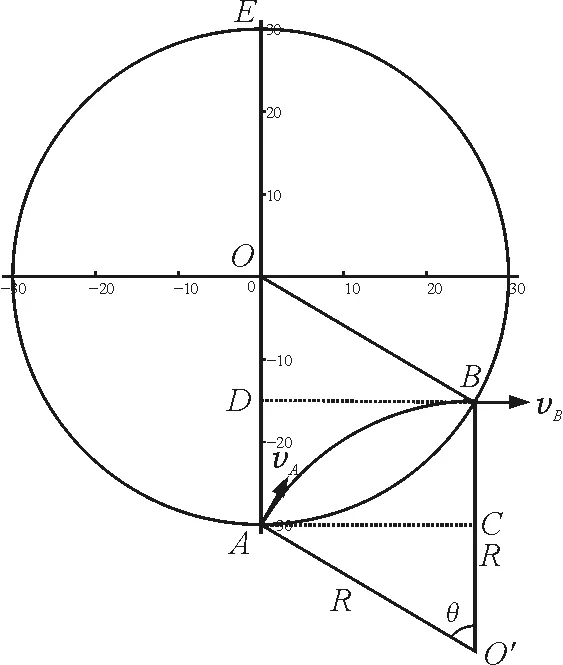
图3 结论2情形1分析图
证明:如图4所示,过B点作vB的反向延长线BC,O和O′为磁场圆与轨迹圆的圆心,AO=BO=BO′=AO′=R,四边形AOBO′为菱形,BO′∥AO,即BO′∥AD,而vB⊥BO′,故vB⊥AD(直径),另AE⊥AD(直径),vB∥AE.
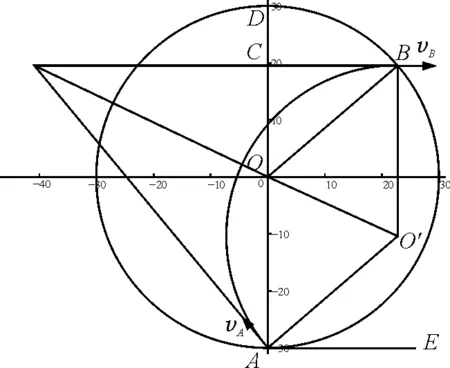
图4 结论2情形2分析图
结论3:大量相同的带电粒子以速率v从圆形匀强磁场边界任意位置以任意方向进入磁场,则所有带电粒子离开磁场时速度方向必相同(平行).
证明:如图5所示,由结论2的证明可知,从相同点入射的速率相同方向不同的带电粒子出射方向均与同一直径垂直或与入射点的同一切线平行,故带电粒子出磁场的出射速度方向必互相平行.
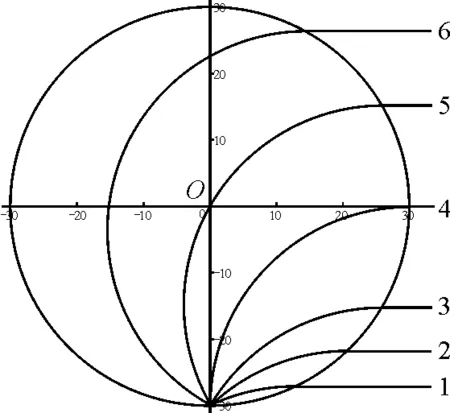
图5 结论3分析图
结论4:带电粒子以速率v从圆形匀强磁场边界任意位置以任意方向进入磁场,离开磁场时的速度方向与进入磁场时位置的垂直高度距离y最大值不超过2R,且满足下列关系.
y=R(1-cosθ)
或
y=R[1+cos (π-θ)]
或
证明:以入射点A作为坐标原点,A点磁场圆切线为x轴,直径为y轴,建立平面直角坐标系,设入射速度vA与x轴的夹角为θ.
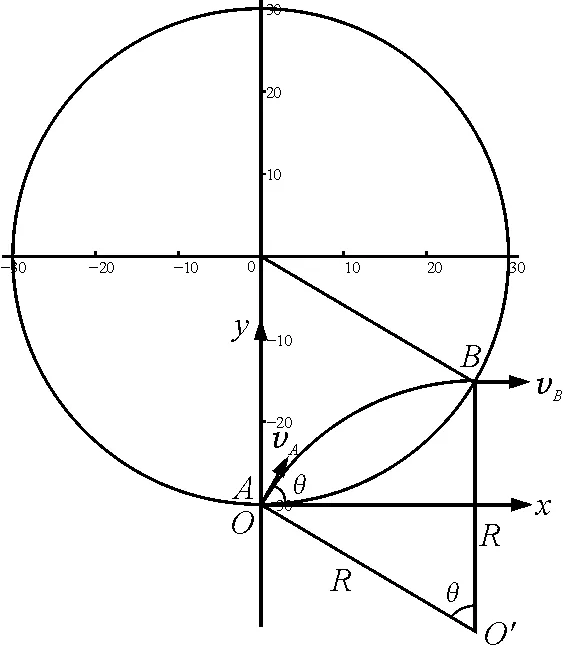
图6 结论4当时的分析图
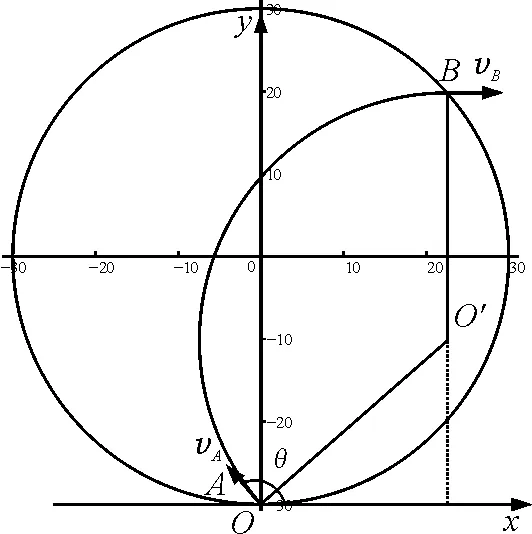
图7 结论4当时的分析图
从图7易知:就算入射角θ=π,即假如粒子能沿着磁场边界做圆周运动,则y=2R,因此,带电粒子离开磁场时的速度方向与进入磁场时位置的垂直高度距离y最大值不超过2R.
结论5:从圆形匀强磁场边界任意位置以任意方向速度v进入磁场的带电粒子1运动轨迹与以该粒子出磁场时的速度v反方向且速度等大进入圆形匀强磁场区域中带电粒子2轨迹之和为定值s1+s2=πR,且带电粒子1的入射点和带电粒子2的出射点分别在磁场圆直径的两端点.
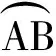
图8 结论5证明分析图
仿真实验检验如图9,图10,图11所示.
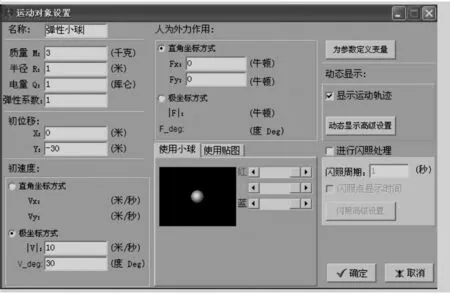
图9 运动对象设置
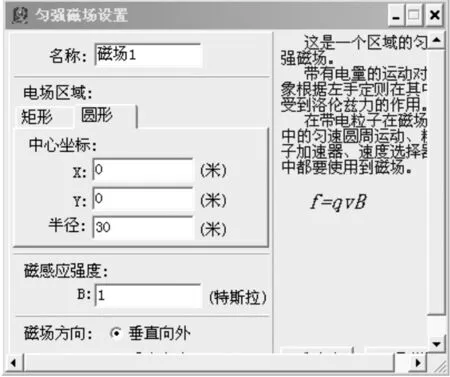
图10 匀强磁场设置
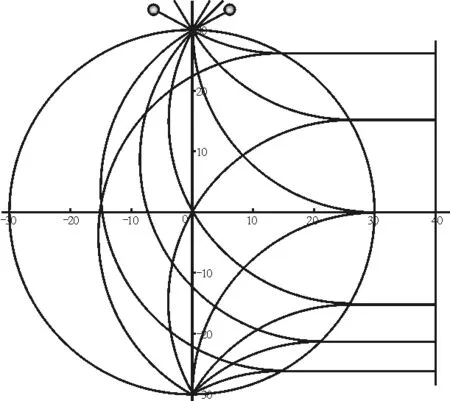
图11 模拟结果
取磁场磁感应强度大小B=1 T,磁场半径R=30 m,带电小球质量M=3 kg,Q=1 C,弹性系数为1,在磁场右边设置一块竖直的弹性挡板,分别让多个相同属性的带电小球(不设重力场)以相同大小的速率v=10 m/s,从A点以不同的入射角θ同时进入磁场,实验发现所有的小球经过与入射点所在的直径平行的弹性挡板反弹之后在直径的另一端同时相遇,与理论预期一致.
5 问题解答
有了以上模型分析得出的结论,下面来解决文中一开始出现的典例.
5.1 分析
第(1)问由题目中“带电粒子从坐标原点O处沿y轴正方向进入磁场后,最终沿圆形磁场区域的水平直径离开磁场并继续沿x轴正方向运动”可知:
其一,带电微粒所受重力必与电场力平衡,洛伦兹力作向心力使得带电微粒做匀速圆周运动.
其二,带电微粒在磁场中做匀速圆周运动的轨迹圆半径与磁场圆半径必相等.
5.2 详细解答
解:(1)由题目中“带电粒子从坐标原点O处沿y轴正方向进入磁场后,最终沿圆形磁场区域的水平直径离开磁场并继续沿x轴正方向运动”可知,带电微粒所受重力与电场力平衡.设电场强度大小为E,由平衡条件得
mg=qE
故
电场方向沿y轴正方向,带电微粒进入磁场后,做匀速圆周运动,且圆运动半径r=R.设匀强磁场的磁感应强度大小为B.由牛顿第二定律得
故
磁场方向垂直于纸面向外.
这样磁场边界上P点的坐标P(x,y)应满足方程:
x=Rsinθy=R(1-cosθ)
所以磁场边界的方程为
x2+(y-R)2=R2
(x-R)2+y2=R2
即为所求磁场的另一侧的边,因此,符合题目要求的最小磁场的范围应是圆x2+(y-R)2=R2与圆(x-R)2+y2=R2的交集部分(图12中阴影部分).由几何关系,可以求得符合条件的磁场的最小面积为
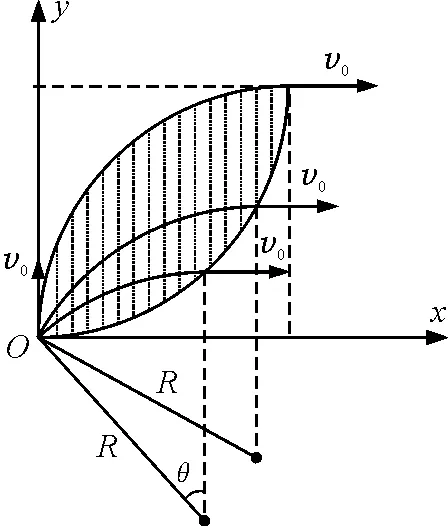
图12 最小磁场范围
