高层建筑施工模拟竖向压缩变形基本原理分析

白 洁 雷 克 葛 杰 孙学锋 鲍 旺

中国建筑第八工程局有限公司 上海 200122

高层建筑是逐层施工完成的，其竖向刚度和竖向荷载（如自重和施工荷载）也是逐层形成的。这种情况与结构刚度一次形成、竖向荷载一次施加的计算方法存在较大差异[1-2]。因此，JGJ 3—2010《高层建筑混凝土结构技术规程》中第5.1.9条明确规定：高层建筑结构在进行重力荷载作用效应分析时，柱、墙、斜撑等构件的轴向变形宜采用适当的计算模型考虑施工状态的影响；复杂高层建筑及房屋高度大于150 m的其他高层建筑结构，应考虑施工状态的影响[3]。

考虑施工状态与一次性加载计算得到的结构内力、位移均不同。以竖向压缩变形为例，即使不考虑混凝土的收缩徐变等与时间相关的因素，一次性加载及考虑施工状态得到的各楼层的竖向位移曲线的典型形状也有明显不同（图1）[4]。由图1可知，一次性加载的竖向压缩变形从结构底部到顶部逐渐增大，最大值在结构顶部；而考虑施工状态的竖向压缩变形从结构底部到顶部先增大再减小，最大值在结构中部，二者存在显著差异。上述2种计算方法得到的结构竖向压缩变形的不同导致了以下2项分析结果的差异：核心筒与外框架竖向压缩变形差、竖向构件压缩变形预调值。

核心筒与外框架竖向压缩变形差直接影响楼面水平度及伸臂桁架的内力；竖向构件压缩变形预调值直接决定了竣工后结构的标高是否符合设计要求。因此，对高层建筑进行施工过程模拟分析很有必要。

图1 竖向压缩变形曲线

目前针对考虑施工状态与一次性建模2种计算方法的对比研究主要有2类。第1类研究直接利用有限元分析软件，对2种计算方法得到的分析结果进行对比，然而并未分析产生上述差异的根本原因[5-6]；第2类研究基于非线性有限元基本原理，通过对有限元方程中刚度矩阵、荷载列阵、位移列阵及边界条件的非线性变换推导出考虑施工状态与一次性建模2种计算方法的差异[7-9]。然而基于非线性有限元的推导过程对力学功底要求较高，一般的技术人员较难理解，在工程实际应用中接受度不高，难以推广。

本文从高层建筑竖向压缩变形的角度入手，研究考虑施工状态与一次性建模2种计算方法产生差异的基本原理。将高层建筑简化为一单杆，采用材料力学基本原理推导其在自重作用下考虑施工状态与否的竖向压缩变形函数，从而得到一次性加载及考虑施工状态的竖向压缩变形曲线。简单而直观地反映了一次性加载及考虑施工状态的竖向压缩变形的基本原理。

1 考虑施工状态的压缩变形函数

本节以图2所示的单杆为例，对考虑施工状态的压缩变形函数进行推导。该单杆长度为l，截面积为A，重度为r，弹性模量为E，第i个微段的自重为Gi。

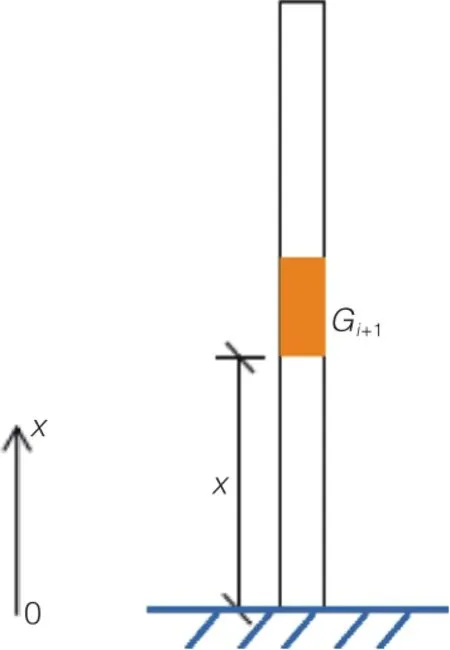
图2 考虑施工状态单杆计算简图

假设结构在第n施工步的完工面标高为x，由于施工时各楼层标高均会找平，故第n施工步的完工面标高x与设计标高一致。设在第n＋1施工步，x标高以上新完工结构自重为Gi＋1，则第n＋1施工步，x标高处新产生竖向位移为：

因此，结构施工到顶后，x标高处合计产生的竖向位移为：

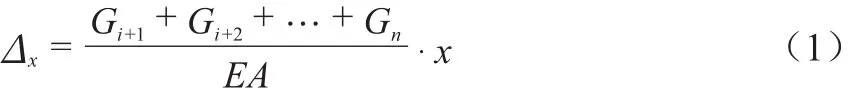
由公式（1）可知，考虑施工状态时，结构完工后高度x处产生的竖向压缩变形值等于高度x以上结构自重对高度为x的部分产生的压缩变形，即：

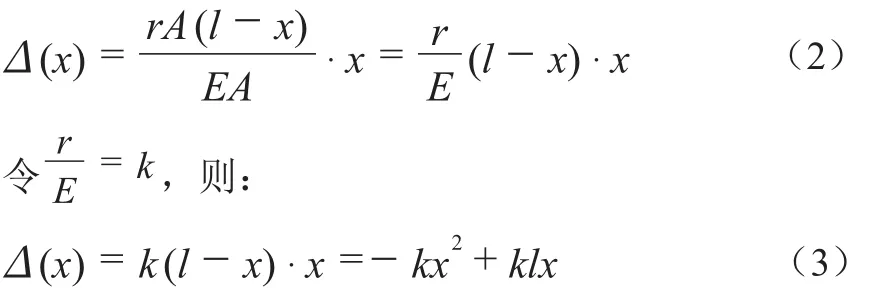
由公式（3）可知，仅计入自重时，考虑施工状态的压缩变形函数为二次函数（图3），压缩变形最大值位于杆件高度l/2处，杆件底部及杆件顶部的压缩变形值为0。

图3 考虑施工状态的单杆压缩变形曲线

2 一次性加载的压缩变形函数

本节以图4所示的单杆为例，对一次性加载的压缩变形函数进行推导。该单杆长度为l，截面积为A，重度为r。

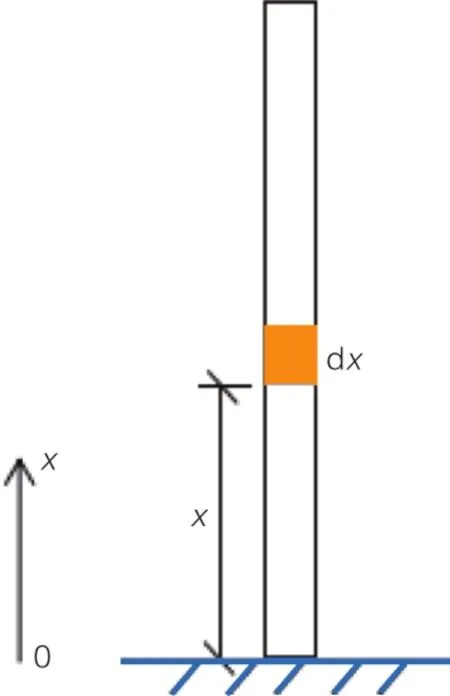
图4 一次性加载单杆计算简图

在距离杆底x高处取出长度为dx的微段，略去该微段自重对变形的影响，则该微段的变形为：

对0到x高度范围的微段变形进行积分，得到一次性加载后高度x处产生的竖向压缩变形[10]，即：

由公式（6）可知，仅计入自重时，一次性加载的压缩变形函数为二次函数（图5），压缩变形最大值位于杆件高度l处，杆件底部压缩变形值为0。

图5 一次性加载的单杆压缩变形曲线

3 算例

一高度为202 m的框架核心筒结构，共55层，利用有限元分析软件MIDAS GEN建立结构模型（图6）。

该塔楼采用核心筒与外框架同步上升的施工方法。在MIDAS模型中，将每3层定义为一个施工步，不考虑混凝土的收缩徐变特性，经施工模拟分析与一次性加载分析，得到核心筒与外框架柱的压缩变形曲线，位移提取点的平面位置分别位于核心筒与框架柱的4个角点处（图7）。

核心筒竖向变形取其4个角点竖向变形的平均值，将一次性加载、施工过程模拟的计算结果进行统计（图8）。

框架柱竖向变形取其4个角点竖向变形的平均值，将一次性加载、施工过程模拟的计算结果进行统计（图9）。

图6 结构模型

图7 位移提取点示意

图8 核心筒竖向变形计算结果

图9 框架柱竖向变形计算结果

由上述分析结果可知，考虑施工状态时，核心筒与外框架的竖向压缩变形曲线大致呈二次函数曲线的形状，最大值在结构中上部；在一次性加载的情况下，核心筒与外框架的竖向压缩变形曲线最大值位于结构顶部。上述竖向压缩变形曲线的整体趋势与本文推导的公式（3）、公式（6）相符。由于实际结构竖向刚度分布不均，以及受混凝土收缩、徐变等时间相关因素的影响，故实际结构的竖向压缩变形曲线不严格遵循二次函数，在考虑施工状态的情况下，竖向压缩变形最大值不位于结构中部，而是位于结构中上部。

4 结语

本文利用材料力学的基本原理，通过将高层建筑简化为一单杆，推导了高层建筑一次性加载及考虑施工状态的竖向压缩变形函数，得到如下结论：

1）考虑施工状态的高层建筑竖向压缩变形函数为公式（3）。由公式（3）可知，考虑施工状态时，结构竖向压缩变形曲线为二次函数曲线，结构底部与顶部压缩变形最小，中部压缩变形最大。

2）一次性加载的高层建筑竖向压缩变形函数为公式（6）。由公式（6）可知，一次性加载时，结构竖向压缩变形曲线也为二次函数曲线，结构底部压缩变形最小，结构顶部压缩变形最大。

3）利用通用有限元软件MIDAS GEN，对一实际工程项目进行考虑施工状态及一次性加载下的竖向压缩变形分析。分析结果表明，实际工程项目的竖向压缩变形曲线与本文推导得到的简化函数曲线基本一致。但由于实际结构存在竖向刚度分布不均，以及受混凝土收缩、徐变等时间相关因素的影响，故其竖向压缩变形曲线不严格遵循二次函数。

本文从根本上揭示了高层建筑一次性加载及考虑施工状态的竖向压缩变形的力学原理，简化了以往采用非线性有限元方法的推导过程，更加便于普通工程技术人员理解、掌握，有利于高层建筑施工过程模拟的推广应用。

此外，本文推导得到的简化计算公式可作为高层建筑竖向压缩变形的手算工具，用来检验软件计算结果的合理性。