新型多用户MIMO-OFDM跨层资源分配算法
2018-10-10周秀秀邓建勋杨世勇
刘 刚, 周秀秀, 邓建勋, 郭 漪, 杨世勇
(西安电子科技大学 a. 通信工程学院; b. 计算机学院, 西安 710071)
0 引 言
随着无线通信的迅速发展, 人们对无线宽带服务需求呈指数型增长, 因此, 在无线频谱资源有限的情况下, 需更先进的技术实现更高的系统频谱效率。多用户多输入多输出-正交频分复用(MIMO-OFDM: Multiple Input Multiple Output-Orthogonal Frequency Division Multiplexing)系统, 将MIMO技术与OFDM技术相结合, 即能有效对抗频率选择性衰落, 又能提高系统容量和频谱效率, 为未来移动通信系统实现提供了技术保证。然而这一结合导致了系统资源调度和分配的难度增加, 因此, 多用户MIMO-OFDM系统中资源分配和调度技术的研究对未来无线通信的发展意义重大, 是近几年的研究热点问题之一。
文献[1,2]通过设计最优能源效率函数进行比特和功率分配, 增大了系统容量、 降低了发射功率。文献[3-7]基于多用户MIMO-OFDM系统下行链路, 在用户速率满足比例公平约束的条件下, 动态地进行功率和载波的分配。在上述资源分配算法中, 都只着重考虑了用户的信道状态信息, 却忽略了对用户媒体接入控制(MAC: Media Access Control)层队列状态信息的考虑, 如果用户MAC层待传送的数据不足, 会造成系统资源的浪费。文献[8]针对多用户OFDM系统, 实现了对MAC层和物理层的跨层设计。文献[9]将跨层设计运用到多用户 MIMO-OFDM系统中, 综合考虑物理层和MAC层的信息, 在满足不同用户不同业务服务质量(QoS: Quality of Service)要求前提下, 进行跨层的资源分配, 整个资源分配过程是载波和功率分开分配, 虽然算法实现复杂度降低, 但同时也损失了一部分的吞吐量。文献[10,11]针对多用户OFDM系统, 提出了载波和功率的联合分配算法, 虽实现复杂度较高, 但系统吞吐量得到大幅度提高。
笔者针对多用户MIMO-OFDM系统, 提出一种基于最低速率约束的跨层资源分配算法, 该算法首先对用户MAC层的缓存队列建模成有限状态马尔科夫链, 并利用其稳态分布将用户QoS要求即最大分组损耗要求转换为物理层最低速率约束, 在满足最低速率约束和总功率一定的前提下, 以系统吞吐量最大化为目标, 进行物理层子载波和功率的联合分配。与其他方案相比, 笔者的方案既能满足用户的QoS要求, 又兼顾了系统公平性, 同时达到了较高的系统吞吐量。
1 系统模型
图1给出了多用户MIMO-OFDM系统模型, 假设系统有一个基站, 基站端有Nt根发射天线, 有K个用户均匀分布在小区中, 每个用户终端有Nr根接收天线, OFDM子载波总数为N个。这里假设一个子载波只能分配给一个用户。假设发射端可完全获得所有用户的信道状态信息(CSI: Channel State Information), 发射端通过利用综合了物理层信道情况、 系统中所有用户MAC层队列情况、 系统中所有用户QoS要求3方面信息的调度与资源分配算法, 对各用户进行调度及给用户合理有效地分配资源。资源分配完成后,K个用户的数据信息加载到其已分配到的载波上并进行自适应调制, 然后将每个子信道上的信号乘以波束成形矢量再送到Nt根发射天线上发射。信号发送完成后, 接收端先将Nr根接收天线接收到的信号乘以相应的接收权重矢量, 然后基于一定的准则对信号进行叠加合并成每个载波上的接收数据, 然后进行相应的自适应解调, 最后提取恢复出第K个用户的数据流。

图1 多用户MIMO-OFDM系统模型Fig.1 Multiuser MIMO-OFDM system model
2 最低速率约束下的跨层资源分配算法
2.1 用户MAC层队列状态和QoS分析
假设系统中所有用户的队列按照先进先出(FIFO: First Input First Output)的方式传输数据, 并且在一帧的持续时间内队列状态保持不变。以某一特定的用户k为例, 假设它的最大队长为Bk, 第t帧的到达分组数为Ak(t), 且服从泊松分布, 队列状态为Qk(t), 接收服务的速率为Rk(t)。文献[7]通过对MAC层的队列进行马尔可夫状态分析, 得到当t→∞时丢包率
(1)

2.2 载波和功率联合分配算法
给出物理层载波和载波上功率联合分配问题的数学模型
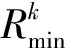
hk,n=(β1/(β1+β2+…+βM))ρk,n,1+…+(βM/(β1+β2+…+βM))ρk,n,M(3)

(4)
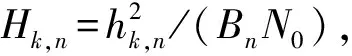
(5)
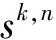
(6)
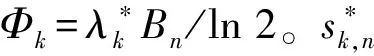
(7)
综上所述, 算法具体步骤如下。
第1步
初始化。令A={1,2,…,N}表示子载波编号集,B={1,2,…K}表示用户集,Ωk表示用户k获得的子载波集合,k=1,2,…,K, 初始化Ωk=Ø,B*=B。
第2步
分配首子载波。当B*≠φ时, 循环执行:

第3步
剩余子载波分配。


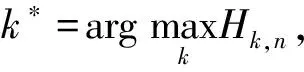
上述步骤完成后, 可知用户获得的子载波及为实现最低速率约束各载波上分配的功率。总发射功率去掉实现最低速率约束所消耗总功率后剩余的功率要用来最大化吞吐量, 基于此, 对载波上的功率进行再分配, 2)转化为一个连续优化问题
(8)
上述问题满足凸优化条件, 拉格朗日函数为

(9)

物理层各载波和各载波上功率分配完毕后, 给出各载波的等效子信道上的功率分配问题的数学模型
(10)
其中λ,μ分别是对应C1,C2两个约束条件的拉格朗日因子。由KKT条件可得用户k在载波n的第m个等效子信道上分配到的功率
pk,n,m=max(Bn,m/μ*ln 2-1/Hk,n,m,0)(11)
3 仿真与分析
系统仿真参数的设置如表1所示。系统基站端有Nt根发射天线, 接收端有K个用户, 每个用户有Nr根接收天线, 可用传输总功率为PT。系统总带宽1 MHz, 分为64个子载波, 采用6径独立的瑞利衰落信道。

表1 系统仿真参数

图2 分组损耗与传输速率关系图Fig.2 Relationship between packet loss and transmission rate
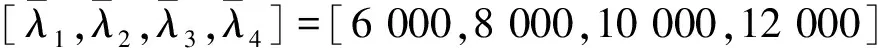
图3为Nt=4,Nr=4,K=4,PT=1 W时, 3种方案所得到的各用户最终速率的比较图。从图3中可知: 文献[5]、 文献[6]的算法与笔者算法得到的每个用户的速率都达到了各自所要求的最低速率约束, 依据2.1节的分析, 已知用户的最低速率约束是由用户的QoS要求(最大分组损耗)转化而来的, 因此也就是满足了各用户的QoS要求。且相比文献[5]和文献[6]中的算法, 笔者算法还使系统中每个用户的最终速率有了很大程度的提升。
图4为用户数K=4时, 在发射、 接收天线的数目不同的情况下, 系统的总传输速率与总传输功率的关系图, 得到如下结论。
1) 文献[5]、 文献[6]以及笔者算法在Nt=4,Nr=4情况下得到的系统总传输速率都比Nt=2,Nr=2的情况下得到的系统总传输速率要高, 即随天线数的增加系统的吞吐量也随之增加。
2) 不论Nt=2,Nr=2的情况, 还是Nt=4,Nr=4的情况, 文献[5]、 文献[6]以及笔者算法得到的系统总传输速率都是随总传输功率的增大而增大, 但文献[5]的总传输速率增大的幅度不大, 文献[6]和笔者算法的总传输速率增大的幅度比较大; 并且笔者算法得到的系统的总传输速率比文献[6]有很大程度的提升。通过上面的分析, 可知笔者算法明显优于文献[5]和文献[6]。

图3 PT=1 W时, 各用户最终速率的比较图 图4 不同天线数下系统总传输速率与总 传输功率的关系图 Fig.3 Comparison of final rate ofeach user when PT=1 W Fig.4 The relationship between the total transmission rate and the total transmission power of the system under different antenna numbers
4 结 语
在多用户MIMO-OFDM系统中, 笔者以最大化系统的吞吐量为目标, 在系统发射总功率一定的条件下, 提出了一种基于最低速率约束的跨层资源分配算法。既兼顾了用户的QoS要求和公平性, 又避免了由于分层设计信息不完整造成的资源分配不合理, 同时还提高系统吞吐量。仿真结果及理论分析表明, 相比传统方案, 笔者提出跨层资源分配算法可以明显提高系统的吞吐量。
