模糊综合评判的系统聚类算法研究

邹晨红, 袁 满

(东北石油大学 计算机与信息技术学院, 黑龙江 大庆 163318)

0 引 言

聚类分析又称群分析, 是一种无监督学习技术, 它能从看似无规律的数据中挖掘出隐藏的数据分布规律。聚类是在对数据进行分组时, 不需要预先给定分组规则, 它能根据数据的特征, 自动地判断每个数据应当归属的群组[1]。目前, 在模式识别[2]、 心理学[3]、 社会科学[4]、 生物学[5]、 数据挖掘[6]、 信息检索[7]和机器学习等领域扮演着越来越重要的角色。随着信息技术的发展, 大数据时代对人类的数据驾驭能力提出了新的挑战, 也为人们获得更为深刻、 全面的洞察能力提供前所未有的空间与潜力。大数据环境下, 数据呈现海量性、 多样性、 高速性和易变性等特点, 对数据聚类也提出了新的挑战。

模糊综合评判是一种基于模糊数学对受到多种因素制约的事物或对象做出总体评价的方法, 自Zadeh[8]建立了模糊数学以来, 模糊综合评判就成为解决各种问题强有力的工具, 并被广泛运用于气象、 教育、 管理科学、 经济学、 社会学和工学等多个领域[9]。在面向大数据时代今天, 事物或对象受多种因素制约, 不同时间或空间, 对象的属性可能会发生变化, 事物或对象制约因素的多样性给数据分析带来了巨大的挑战, 因此模糊综合评判的数据处理方法被广泛应用于大数据分析中, 模糊综合评判可以对多维性的事物或对象进行全面分析, 并人工赋予权重, 具有整体性、 可操作性、 简略性[10]等特点。但在使用模糊综合评判方法进行聚类分析时, 发现基于模糊综合评判的聚类结果不准确, 聚类个数难以控制等。针对上述问题, 笔者提出一种基于模糊综合评判的系统聚类算法, 该方法在对受多种因素制约的事物或对象进行聚类前, 运用模糊综合评判进行数据处理, 对制约因素进行模糊矩阵的构建, 并根据实际情况人为设置权重, 使该算法具有可操控性； 然后选择合适的矩阵合成算子进行隶属度计算； 最后进行系统聚类。系统聚类是聚类中常用的一种聚类方法, 聚类中能详细地看出聚类的过程以及类与类间距, 但针对数据量较大、 维度较多的事物或对象聚类较复杂问题, 经过模糊综合评判的处理, 使该算法变得简单, 易于实施。

知识经济时代, 教育对国家的发展和社会的进步起到了至关重要的作用, 许多国家把教育质量视为提升国际竞争力, 实现国家长期战略目标的关键； 加强管理、 保障教学质量、 促进教学改革, 是不断提升人才培养质量的重要手段[11], 因此重视和加强教学评价已成为教育发展的普遍趋势。学生成绩是教育与教学管理工作中的重要环节, 不仅是衡量学生对知识的掌握程度的重要数据来源, 也是评估教学质量的重要参考信息来源[12]。但是班级成绩具有数据量较大、 维度较多等特点, 进行聚类分析时具有一定的复杂性, 因此笔者以班级考试成绩为例进行实验分析, 验证了该算法的准确性、 整体性、 可操控性、 简略性等特点。

1 模糊综合评判优化系统聚类算法的相关研究

1.1 模糊综合评判

模糊综合评判是汪培庄教授[13]提出的一种模糊数学的应用方法, 是一种应用模糊数据实现关系合成的原理, 即从多个角度对事物进行综合判断, 并能人为设定各个因素的影响权重。

1) 模糊集合的概念。模糊集合是由Zadeh[8]于1965年提出的, 采用隶属程度的思想描述差异的中间过度, 其模糊子集的定义为给定论域U, 如果给定一个映射

就确定一个模糊集A, 其映射μA称为模糊集A的隶属函数,μ(x)称为x对模糊集A的隶属度。使μA(x)=0.5的点x0称为模糊集A的过渡点, 即是模糊性最大的点。

对一个确定的论域U可以有多个不同的模糊集, 记U上的模糊集的全体为F(U), 即

F(U)={A|μA:U→[0,1]}

即F(U)就是论域U上的模糊幂集, 且U⊆F(U)。

2) 模糊集合的运算法则。模糊集合之间的运算, 实际上是每个元素对隶属度做运算, 根据实际的应用背景, 选择运算算子。常用的矩阵合成算子有以下4种。

M(∧,∨)算子

(1)

式(1)是Zadeh算子, 又称“取大取小算子”, 在模糊综合评判中, 由于取大取小有很好的代数性质, 而且算法思路清晰、 运算简单、 易于掌握。该方法权数作用较弱, 综合程度较弱, 主因素突出。

M(·,∨)算子

(2)

式(2)是最大乘积算子, 评判问题应满足： 因素集中的各因子是相互独立的, 且各因素间不能相互补偿, 权数作用比较明显, 也是主因素突出型。

M(∧,⊕)算子

(3)

式(3)权数不明显, 综合程度较强, 属于加权平均型。

M(·,⊕)算子

(4)

式(4)权数较明显, 综合程度较强, 为加权平均型。

3) 模糊综合评判实现过程。模糊综合评判在实施过程中考虑到了多种影响因素, 解决了很多传统计算方法中难以处理的实际问题, 根据因素的多少及复杂性将模型综合评判分为单级模糊综合评判和多级模糊综合评判。其中单级模糊综合评判流程如图1所示。

图1 单级模糊综合评判流程图Fig.1 Single-stage fuzzy comprehensive evaluation flow chart

由图1可看出, 模糊综合评判算法流程：

1) 数据标准化。为消除数据量纲的影响, 对原始数据进行标准化处理；

2) 取因数集。U={u1,u2,…,un}, 选取被评价对象的评价指标；

3) 取评语集。V={v1,v2,…,vm}, 确定评价结果的等级；

4) 确定各因素的权重。A={a1,a2,…,an}, 赋予各个因数权重；

5) 确定模糊综合评判矩阵： 对每个因素ui作出评价；

6) 利用式(1)～式(4)中的任意算子进行矩阵合成, 计算隶属度并判断结果, 由此判断评价的最终结果。

多级模型综合评判需要结合具体问题进行不同层次的单级模糊综合评判, 然后根据需要逐级进行评判, 最终综合成总的评判结果。

模糊综合评判突出权数的作用, 评价者可根据实际需求对评价因数赋予权值, 综合程度较强； 通过计算对被评价对象呈现的模糊性做出了比较合理、 科学的量化评价, 是目前在各个领域常用的一种综合的评价方法。由于模糊综合评判在实施前, 对评价结果进行了等级设定, 因此大多人很容易将评价结果作为分类的结果, 此方法虽然能对评价对象作出综合的评价, 但是在分类、 聚类中还具有一定局限性。

1.2 系统聚类

系统聚类是聚类方法中的一种比较常用的聚类方法, 其基本思想是假设每个样品各自成一类, 然后进行类间距离进行计算, 将距离最近的两个类合并为一个新类； 再计算新类与其他类之间的距离, 将距离最近的类合并为新类, 以此类推, 直至所有的类都合并为一类； 最后根据需要确定最终的聚类结果[14]。

1) 数据标准化。当指标变量的量纲不同或数量级相差很大时, 常须对数据进行标准化, 常用的标准化方法有标准化变换、 极差标准化变换、 均值标准化变换和标准差标准变换。

2) 对象之间的距离。主要有以下距离计算方法。

绝对距离

(5)

欧氏距离

(6)

明考斯基距离

(7)

兰氏距离

(8)

切比雪夫距离

(9)

3) 类间距离。对象与类以及类与类之间的距离, 通常情况, 对于任意两个类之间的度量, 有以下4种方法。

① 最小距离。是指用两个聚类所有数据点的最近距离代表两个类的距离, 表示为

(10)

② 最大距离。是指用两个聚类所有数据点的最远距离代表两个类的距离, 表示为

(11)

③ 平均值距离。是指用两个聚类各自中心点之间的距离代表两个聚类之间的距离, 表示为

dmean(Ci,Cj)=|mi-mj|

(12)

其中mi是类Ci的平均值,mj是类Cj的平均值。

④ 平均距离。是指用两个聚类所有数据点之间的距离的平均距离代表两个聚类的距离, 表示为

(13)

4) 系统聚类流程。系统聚类算法流程：

① 对原始数据进行标准化处理, 消除量纲的影响, 并构建数据矩阵；

② 将每个对象看成一个类, 由式(5)～式(9)中任意一个距离公式计算每两个对象之间的距离, 构建相异度矩阵；

③ 把两个距离最近的类聚集为一个新类, 并更新类的个数； 用式(10)～式(13)中的任意一个距离计算方法计算类之间的距离, 更新相异度矩阵；

④ 重复执行步骤(3), 直至全部类合并到一个类中或达到要求的聚类个数；

⑤ 结束, 输出聚类结果。

系统聚类法将研究对象作为一个系统, 按照分解、 比较、 综合的思维进行决策, 尤其是对无结构、 多目标、 多准则等进行综合评价, 一方面简单实用, 没有片面的注重行为、 逻辑、 推理, 而是将定性方法与定量方法有机地结合, 使复杂的系统分解, 便于实现； 另一方面系统聚类比一般的定量方法更讲求定性的分析和判断。但系统聚类方法在实际的应用中不能为决策者直接提供较好的决策方案； 当定量数据较少、 定性成分较多时, 不易令人信服, 当指标过多时, 数据统计量较大, 权重难以确定。

2 模糊综合评判优化的系统聚类

笔者针对上述问题, 提出一种模糊系统聚类方法, 该方法前期阶段运用模糊综合评判计算评价对象的隶属度, 并对隶属度结果进行聚类, 从而实现复杂对象的精准聚类。假定评语集有m个, 因素集有n个, 聚类对象的个数有s个, 基于模糊综合评判的系统聚类实现步骤如下。

Step1 取因素集U={u1,u2,…un}、 评语集V={v1,v2,…vm}, 并确定每个因数的权重A={a1,a2,…,an}, 构建模糊矩阵, 即

(14)

Step2 运用式(1)～式(4)中任意矩阵合成算子进行矩阵合成运算, 计算得隶属度

(15)

其中∘表示算子。

Step3 构建数据矩阵, 将计算结果式(15)作为输入, 构建数据矩阵, 即

(16)

Step4 运用式(5)～式(9)中任意公式计算矩阵(12)中的每个对象之间的距离, 构建相异度矩阵

(17)

Step5 选择并更新矩阵(17), 通过相异度矩阵查找相近的两个类, 将其合并为一个新类, 运用式(10)～式(13)中的任意公式计算类与类之间的距离, 更新相异度矩阵。

Step6 重复执行步骤Step5, 直至当前全部的对象都聚为一个类或满足给定个数为止。

Step7 输出聚类结果。

3 实例分析

在面向教育大数据的今天, 客观、 公正、 合理的对学生成绩进行评价, 挖掘出隐藏在成绩中更多的信息, 对学校教育和管理的提升具有良好的意义[15]。下面以某中学5个班级的4次考试成绩为研究对象, 对班级进行聚类分析, 由于班级人数较多, 学校进行考试也比较频繁, 影响考试的因素较多, 其权重可能会不一样, 因此根据班级成绩对班级进行聚类分析具有一定的复杂性, 所以以此为例验证模糊综合评判优化系统聚类的有效性。

3.1 数据准备

选取4次考试成绩, 其因素集为U={u1,u2,u3,u4}； 取评价因素集的权重为A={0.2,0.3,0.2,0.3}； 确定评价对象的评语集, 将评价对象分为4个等级, 即优秀、 良好、 一般、 差这4个等级, 即V={优秀v1,良好v2,一般v3,差v4}。根据成绩得到每个班级的模糊矩阵为

3.2 矩阵合成

根据算子的特点, 选择算子M(·,⊕)进行矩阵合成计算, 计算结果为

3.3 系统聚类

由以上结果可知, 如果直接根据模糊综合评判进行聚类则具有一定的局限性, 为提高聚类的准确性, 在模糊综合评判的基础上, 根据笔者提出基于模糊综合评判的系统聚类方法, 即对计算结果进行系统聚类。对上述结果构建数据集, 即

本实验运用SPSS工具实现聚类, 将上述数据矩阵写入SPSS, 如图2所示。对以上数据进行系统聚类分析, 聚类系谱图如图3所示。

图2 SPSS数据集Fig.2 SPSS data set

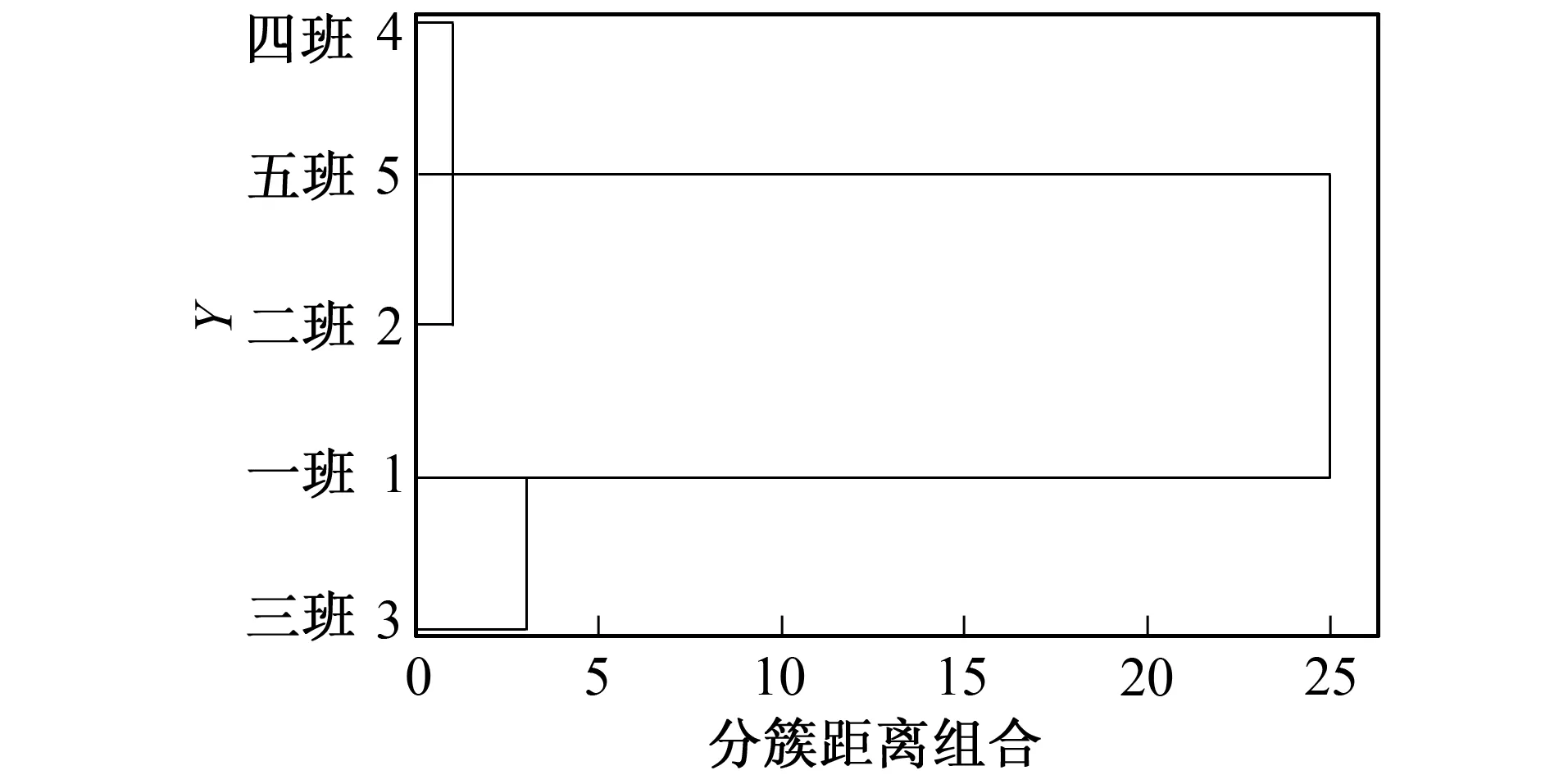
图3 系统聚类谱系图 Fig.3 System clustering of hierarchical diagram

3.4 实验结果分析

由矩阵合成算子计算结果可知, 若利用模糊综合评判对5个班级进行分类, 则他们都属于良好的一类, 即从整体对各个班级进行评价, 各个班级的成绩良好, 教学效果比较好, 但不能从根本上对其进行聚类； 而在隶属度判断的基础上进行系统聚类, 由聚类谱系图可知该系统聚类的详细过程, 以及聚类过程中样品间的距离, 并且可以人为选择聚类结果的个数, 如果将其分为两类, 用C表示类, 则为

C1={一班, 三班},C2={二班, 四班, 五班}

根据班级的实际情况, 上述5个班级中的一班与三班的成绩中, 优秀、 良好、 一般与差各个等级的占比相近, 二班、 四班、 五班这3个班级的各个等级占比比较相近。因此此种方法的聚类结果比较准确, 所以模糊系统聚类的方法是切实可行的。

通过以上实验验证, 运用基于模糊综合评判的系统聚类算法对复杂的综合性的评价对象进行评价与分析是可行的, 由实验可得知, 该算法具有以下特性。

1) 准确性。是评价评价模型的一个重要的指标, 评价模型的准确性直接影响评价结果及分析结果, 分析模型越准确, 结果越具有意义。由观察可知, 若将上述5个班级分为两类, 根据5个班级在各个等级的占比可知, 一班与三班为一类, 其余3个班级为另一类, 与实验结果相符。若直接根据模糊综合评判结果进行聚类, 则不能达到此效果。因此基于模糊综合评判的系统聚类算法具有准确性。

2) 整体性。实验选择班级的4次考试成绩, 并涵盖班级全部成员, 即对班级的全部成员进行了综合考虑, 具有整体性。

3) 可操控性。在指标的选取过程中, 可人为选取评价指标, 并能对多次考试成绩的权重进行赋值, 实验最后还能任意选取聚类个数, 即在整个实验中, 都可以人为控制； 模型的参数具有可操控性、 灵活性, 其适应性较强。

4) 简略性。在评价过程中, 由于指标因素较多、 学生人数较多导致评价过程中涉及的数据较多, 计算量比较大、 比较复杂, 容易导致数据错误以至于评价结果的不准确性, 而本实验中采用的均为经典算法, 在系统聚类之前融合了模糊综合评判算法, 算法相对来说比较简单, 易于理解。

4 结 语

笔者针对传统经典算法模糊综合评判以及系统聚类在进行聚类中存在的片面性、 复杂性提出了一种基于模糊综合评判的系统聚类算法, 该方法首先采用模糊综合评判对复杂数据进行综合处理, 然后运用系统聚类对处理结果进行系统聚类, 提高了聚类的准确性。最后笔者通过对5个班级的4次考试成绩验证了该方法的有效性, 并对分析结果进行了总结, 得出基于模糊综合评判的系统聚类算法具有准确性、 整体性、 可操控性以及简略性等特点。