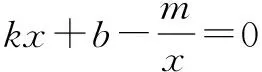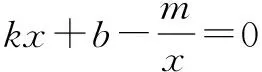利用数形结合分析一次函数和反比例函数的关系

陈礼弦

(贵州省贵安新区中八二小 550003)

在实施基础教育课程改革的今天，上初中数学的各位同仁都知道，一次函数和反比例函数的关系是初中数学教学的一个重点，在每年的中考试卷之中，至少有10分相关的题目出现，许多学生对这一问题，难以下笔.根据我多年的教学研究，利用数形结合来分析这一问题，使问题从复杂变简单，从抽象变形象，教学会有事半功倍之效.

一、什么是数形结合

数形结合是代数与图形相结合的数学思想，利用代数解决图形问题或利用图形解决代数问题，灵活运用能解决很多问题.

二、利用数形结合分析一次函数和反比例函数的关系

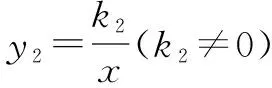
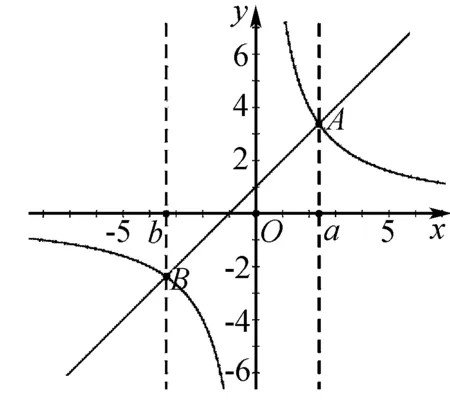
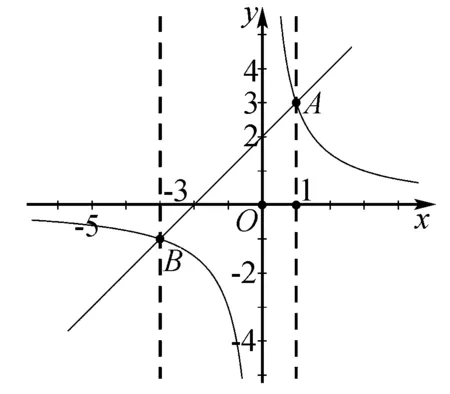
1.根据图象，可以把图象分成四个区间

第一区间：位置：左边虚线之左；反比例函数的图象在一次函数的图象的上边；xy1(反比例函数的值大于一次函数的值或一次函数的值小于反比例函数的值).

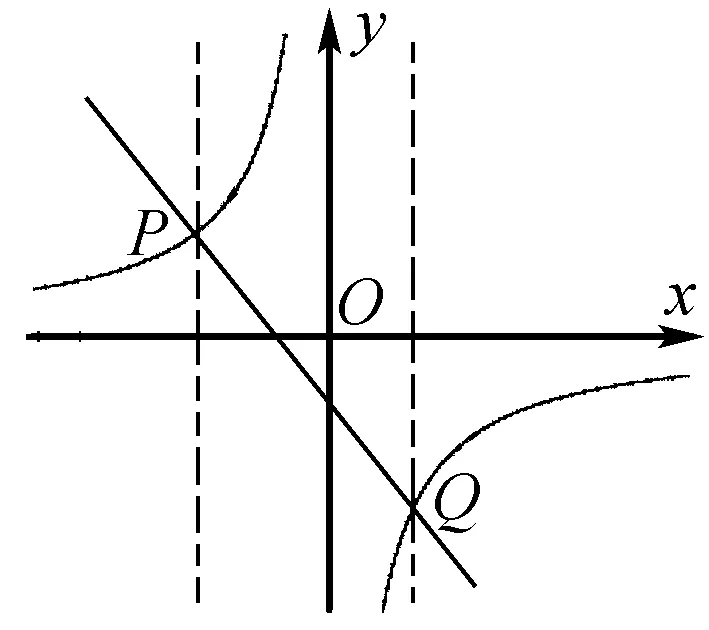
第二区间：位置：左边虚线和y轴之间；反比例函数的图象在一次函数的图象的下边；b

第三区间：位置：y轴和右边虚线之间；反比例函数的图象在一次函数的图象的上边；0y1(反比例函数的值大于一次函数的值或一次函数的值小于反比例函数的值).

第四区间：位置：右边虚线之右；反比例函数的图象在一次函数的图象的下边；x>a，y2

2、根据图象，一次函数的图象和反比例函数的图象交于A点和B点，此时，x=a或x=b；y2=y1(一次函数的值等于反比例函数的值).

三、举例说明

(2)不等式kx+b-mx<0的解集是____.

(1)求反比例函数和一次函数的解析式；

(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围．

(2)问一次函数的值大于反比例函数的值的x的取值范围，那么一次函数的图象在反比例函数的图象的上边，根据图象可知，在

第一区间和第三区间，一次函数的图象在反比例函数的图象的上边，在第一区间时，x<-2；在第三区间时，0

总之，如果你利用数形结合的方法引导学生分析一次函数和反比例函数的关系，那么你的教学便达到授人以渔，教是为了不教的效果.