图的最大匹配个数的下界
2018-10-09翟绍辉郭利涛郑艺容
翟绍辉,郭利涛,郑艺容,庄 蔚
(厦门理工学院应用数学学院,福建厦门361024)
1 预备知识
本文中所讨论的图都是简单图,未定义的符号请参阅文献[1-2].
设G是一个具有n个顶点的图,V(G)和E(G)分别表示G中的顶点集和边集.如果G中某个顶点的度数为零,则称该顶点为孤立点.设M是E(G)的一个子集,若M中任意两条边都没有公共顶点,则称M是G的一个匹配.如果|M|=k≥1,则称M是G的一个k-匹配,这里|M|表示M中边的个数.特别地,如果G中没有匹配M′使得|M′|>|M|,则称M是G中的最大匹配.设v是G中任意一点,若v与M中的某条边相关联,则称M饱和v.如果M是G中的最大匹配且|M|=k,那么G中恰有(n-2k)个顶点未被M饱和,因此也称该k-匹配M是亏(n-2k)-匹配.特别地,若n-2k=0或n-2k=1,则分别称M是G的完美匹配或几乎完美匹配.令m(G)表示G中最大匹配个数,特别地,如果G有完美匹配,则用pm(G)表示G中完美匹配个数.
若G是一个具有完美匹配的图,则有pm(G)≥ 1.当pm(G)=1时,即G具有唯一完美匹配时,下面定理给出了这类图的刻画.
定理1[2,Corollary 5.3.12]一个图G有唯一完美匹配的充分必要条件是G可以通过以下递归方式构造出来:设G1和G2是两个点不交的图,且都具有唯一的完美匹配,设x1和x2是两个新点,连接xi和Gi中的至少一个点,并且连接x1和x2,这里i=1,2.
特别的,对于无割边三正则图,Petersen[3]证明了这类图有完美匹配.Lovsz等[2,Conjecture 8.1.8]给出了下面的猜想
猜想1[2]存在一个正整数0<ε<1,使得对任意无割边三正则图G,有
pm(G)≥2ε|V(G)|.
目前,这个猜想仍然没有被解决,现已有的相关结论可以参考文献[3-7]等.另外,关于特殊图类(例如:树)的最大匹配的计数问题,也有一些相关的研究,详见文献[8-9]等.
本文中考虑的图是具有最大匹配(不是完美匹配)的一般图,证明了任意具有n个顶点且最大匹配为k-匹配的连通图都至少有n-2k+1个互不相同的最大匹配,这里n≥2k+1.另外,还刻画了恰好具有n-2k+1个最大匹配的图.
为了证明本文中的主要结论,需要引入下面一些定义符号和已知的结论.假设S是V(G)的一个子集,NG(S)表示V(G)中所有与S中顶点相邻的顶点集合.Hall[10]给出了下面结论.
定理2[10]二部图G=(A,B)有饱和A中所有顶点的最大匹配的充分必要条件是对任意S⊆A,有|NG(S)|≥|S|.
设G=(A,B)是一个二部图,如果对任意非空集合S⊂A都有|NG(S)|>|S|成立,则称G有正盈余(对于A).根据定理2,若G=(A,B)是二部图且对A有正盈余,则G有饱和A中所有顶点的最大匹配.
设G是一个具有n个顶点的图,若任意删去G中p个顶点后余图都有完美匹配,则称G是p-因子临界图.特别地,若p=1,则称G是因子临界图.设S是V(G)的一个子集,G[S]表示由S导出的子图.令D(G)表示V(G)中所有至少被G中某个最大匹配未饱和的顶点所组成的集合,A(G)表示V(G)-D(G)中至少与D(G)中一个顶点相邻的顶点集合,C(G)=V(G)-D(G)-A(G).删去C(G)中所有顶点和由A(G)在G中导出子图的边,并且分别收缩D(G)的导出子图的每个分支为一个顶点,则所得到的新图记为B(G).
定理3[2,Theorem 3.2.1](Gallai-Edmonds结构定理)设G是一个图,D(G),A(G),C(G)和B(G)如上述所定义,则有以下结论成立:
(i)D(G)的导出子图的每一个分支都是因子临界的;
(ii)C(G)的导出子图都有完美匹配;
(iii)B(G)是二部图并且有正盈余(对于A(G));
(iv)G的最大匹配包含D(G)中每个分支的几乎完美匹配,C(G)中每个分支的完美匹配和饱和A(G)中所有顶点与D(G)中不同分支的匹配;

2 主要结论
定理4设G是一个具有n个顶点,最大匹配为k-匹配且没有孤立点的连通图,则有m(G)≥n-2k+1,这里n≥2k+1.
证明设M是G的一个最大匹配且有|M|=k,v1,…,vn-2k是没有被M饱和的顶点集合.由于M是G的最大匹配,则由v1,…,vn-2k在G中的导出子图G[v1,…,vn-2k]是空图.又因为G中没有孤立点,所以对每个vi都存在有一边ei连接vi和V(M)中的某个点,不妨设该点为ui,这里i∈{1,2,…,n-2k}.设f是M中的一边且饱和ui,则可以得到一个不同于M的最大匹配Mvi=M-{f}∪{ei}.类似地,可以得到至少n-2k个互不相同的最大匹配Mv1,…,Mvn-2k,且都不同于M.因此有m(G)≥n-2k+1成立,证毕.
根据二部图正盈余的定义,可以得到如下结论.
引理1设G=(A,B)是一个二部图并且对A有正盈余,则G的任意一边都包含在G中的某个最大匹配中.
证明设e=uv是G中任意一边,不妨进一步假设u∈A,v∈B.令A′=A-{u},B′=B-{v}和G′=(A′,B′).对任意S⊆A′有|NG′(S)|+1≥|NG(S)|成立.由于G对A有正盈余,则有|NG(S)|>|S|.综合上述两个式子可以得到|NG′(S)|≥|S|,根据定理2,则G′有最大匹配且饱和A′中的所有顶点.不妨设该最大匹配为M′,令M=M′∪{e},则M是G中的最大匹配且包含e.因此G的任意一边都包含在G中的某个最大匹配中,证毕.
引理2设G是一个具有n个顶点且最大匹配为k-匹配的连通图,这里n≥2k+1,C(G),A(G),D(G)和B(G)如引言中所定义.设D1,…,Ds是D(G)中的所有分支.若C(G)≠∅,则有m(G)≥pm(C(G))m(B(G))且等号成立的充分必要条件是D1,…,Ds都是单点集.若C(G)=∅,则有m(G)≥m(B(G))且等号成立的充分必要条件是D1,…,Ds都是单点集.
证明这里仅证明C(G)≠∅的情形,对于C(G)=∅的情形可以类似的给出证明,这里不再赘述.根据Gallai-Edmonds结构定理的(iv),容易验证m(G)≥pm(C(G))m(B(G)).下面证明m(G)=pm(C(G))m(B(G))成立的充分必要条件是D1,…,Ds都是单点集.
充分性:当D1,…,Ds都是单点集,容易得到m(G)=pm(C(G))m(B(G))成立.
必要性:反证,不妨假定|D1|≥3.假设u1v1,…,ulvl是G中连接D1和A(G)的边,这里l≥1,u1,…,ul∈A(G),v1,…,vl∈D1.设v∈B(G)是由D1收缩后得到的顶点,那么u1v,…,ulv是B(G)中连接v和A(G)的边.根据Gallai-Edmonds结构定理的(v)可以得到以下不等式
m(G)≥pm(C(G))[m(B(G)-v))m(D1)+
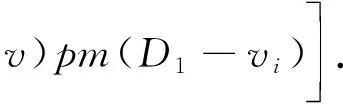
(1)
由于D1是因子临界的,则有pm(D1-vi)≥1成立;由于C(G)≠∅,则pm(C(G))≥1成立;根据定理4,可以得到m(D1)≥2成立.因此式(1)可以化简为
m(G)≥pm(C(G))[m(B(G)-v))+
pm(C(G))m(B(G)-v)).
(2)
已知G是连通图,则根据Gallai-Edmonds结构定理和B(G)的构造方法可知B(G)是没有孤立点的二部图,并且B(G)的最大匹配也是亏(n-2k)-匹配.因为B(G)对A(G)有正盈余,则在B(G)中,A(G)的任意一点的度数都不小于2.因此可以进一步得到B(G)-v也没有孤立点.另外,根据B(G)对A(G)有正盈余和引理1可得B(G)-v有饱和A(G)中所有顶点的最大匹配,并且此时的最大匹配是亏(n-2k-1)-匹配.根据定理4有下面不等式成立
m(B(G)-v))≥n-2k≥1.
根据上述得到的pm(C(G))≥1和m(B(G)-v))≥n-2k≥1,则式(2)可以变为
m(G)≥pm(C(G))[m(B(G)-v))+
1=pm(C(G))m(B(G))+1>
pm(C(G))m(B(G)).
这与m(G)=pm(C(G))m(B(G))矛盾.因此,当m(G)=pm(C(G))m(B(G))时,D1,…,Ds都是单点集,证毕.
对于一个具有n个顶点且最大匹配为k-匹配的连通图G,下面定理刻画了恰好具有n-2k+1个最大匹配的图.
定理5设G是一个具有n个顶点,最大匹配为k-匹配的连通图,且恰好有n-2k+1个互不相同的最大匹配,这里n≥2k+1且k≥1,那么根据Gallai-Edmonds结构定理,G的结构如下:
(i)C(G)具有唯一的完美匹配或C(G)=∅;
(ii)A(G)恰好只有一个点;
(iii)D(G)的每一个分支都是一个单点集.
证明设G恰好只有n-2k+1个互不相同的最大匹配(k-匹配),即m(G)=n-2k+1.根据B(G)的构造方法可知,当G有亏(n-2k)-匹配时,那么B(G)也有亏(n-2k)-匹配.根据定理4有
慕课不断发展的同时对教师的教学能力、专业知识储备量也提出了更高的要求[10]。在传统课堂上,有些教师可能总是重复以往的知识点,而忽略了最新的知识内容。在慕课这个平台上,教师如果想进行问题模式的教学,首要的就是丰富自己的知识。只有教师不断的提升理论水平、实践能力,并将两者融汇贯通,才能有效指导学生完成对知识的分析、整合、归纳、演绎,最终内化于心的过程[11]。并且与此同时,教师不仅可以将自己的专业知识分享给别人,还可以学习到最全面最新颖的知识点,而且还可以自己设计问题和学习者进行线上讨论,通过有趣的学习方法让学生更好的掌握知识,做到了提高自身专业知识的同时,改革了教学方法。
m(B(G))≥n-2k+1.
(3)
根据Gallai-Edmonds结构定理的(i),如果C(G)≠∅,那么C(G)的导出子图有完美匹配,则有
pm(C(G))≥1.
(4)
根据引理2有
m(G)≥pm(C(G))m(B(G)).
(5)
根据m(G)=n-2k+1和式(3)~(5)可以得到m(G)=m(B(G))=n-2k+1和pm(C(G))=1,即C(G)只有唯一的完美匹配.
如果C(G)=∅,那么根据引理2有
(6)
根据m(G)=n-2k+1和式(3),(6)可以得到
m(G)=m(B(G))=n-2k+1.
综上,无论C(G)是否为空集,均有m(B(G))=n-2k+1.根据引理2,可以得到D(G)中每一个分支都是单点集,这就证明了定理中的(i)和(iii).
下面证明(ii).由于k≥1,则A(G)≠∅.现在采用反证法证明A(G)恰好只有一个点.假设A(G)={u1,…,us}且s≥2.根据Gallai-Edmonds结构定理,B(G)是二部图,A(G)和V(B(G))-A(G)恰好是B(G)的一个二部划分.由于G是连通的且最大匹配是亏(n-2k)-匹配,则B(G)没有孤立点且最大匹配也是亏(n-2k)-匹配.由于|A(G)|=s≥2,则可以得到B(G)的最大匹配中边的个数为s.
设M是B(G)的最大匹配(或亏(n-2k)-匹配),则|M|=s≥2.不妨设u1v1∈M,这里v1∈V(B(G))-A(G),u1∈A(G),显然M饱和A(G)中所有点.
情形1B(G)-u1-v1没有孤立点.
此时M-{u1v1}是图B(G)-u1-v1的最大匹配,且也是B(G)-u1-v1的亏(n-2k)-匹配.根据定理4,m(B(G)-u1-v1)≥n-2k+1.设M1,…Mn-2k+1是B(G)-u1-v1中互不相同的最大匹配,则M1∪{u1v1},…,Mn-2k+1∪{u1v1}也是B(G)中互不相同的最大匹配.由于B(G)是二部图且对A(G)有正盈余,则u1在B(G)中至少是2度点.设v2是u1在B(G)中除v1以外的一个邻点,即u1v2∈E(B(G)).根据引理1,B(G)中存在一个最大匹配M′使得u1v2∈M′,且M′不同于M1∪{u1v1},…,Mn-2k+1∪{u1v1}.这样就得到B(G)中n-2k+2个互不相同的最大匹配,这与m(B(G))=n-2k+1矛盾.
情形2B(G)-u1-v1有孤立点.
不妨设w1,…,wt是B(G)-u1-v1中的孤立点,显然,w1,…,wt∈V(B(G))-A(G)-{v1}.由于M-{u1v1}是B(G)-u1-v1的最大匹配,同样也是B(G)-u1-v1的亏(n-2k)-匹配,因此可以得到1≤t≤n-2k.设S表示由点集{w1,…,wt,u1,v1}的导出子图,则S是星图,即在S中顶点u1的度数为t+1,其余顶点度数均为1.容易得到m(S)=t+1且{u1v1},{u1w1},…,{u1wt}分别是S的最大匹配.
(i) 1≤t 此时M-{u1v1}是B(G)-u1-v1的最大匹配,也是B(G)-V(S)中的最大匹配,同样也是B(G)-V(S)的亏(n-2k-t)-匹配,并且B(G)-V(S)没有孤立点.根据定理4,可以得到m(B(G)-V(S))≥n-2k-t+1.另外,容易看出S中任意一个最大匹配和B(G)-V(S)中任意一个最大匹配的并集恰好是B(G)的一个最大匹配,因此有以下不等式成立 m(B(G))≥m(S)m(B(G)-V(S))≥ (t+1)(n-2k-t+1)>n-2k+1, 这与m(B(G))=n-2k+1矛盾. (ii)t=n-2k. 此时M-{u1v1}是图B(G)-V(S)中的完美匹配.由于B(G)是二部图且对A(G)有正盈余,因此S和(B(G)-V(S))∩(A(G)-u1)至少有一边连接.不妨设e是其中一条边,根据引理1,B(G)中存在一个最大匹配包含e,不妨设为Me.则Me,(M-{u1v1})∪{u1v1},(M-{u1v1})∪{u1w1},…,(M-{u1v1})∪{u1wn-2k}均是B(G)中互不相同的最大匹配,且共有n-2k+2个最大匹配,这与m(B(G))=n-2k+1矛盾. 综上各种情形可以得到,A(G)只能有一个单点,这样就证明了(ii),证毕.
