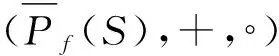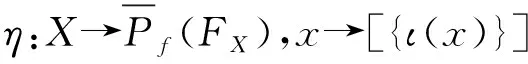Ai-半环簇自由对象模型的刻画
2018-10-09王爱法王丽丽
王爱法,王丽丽
(1. 西北大学数学学院,陕西西安710127;2. 重庆理工大学理学院,重庆400054)
1 预备知识
设(S,+,·)是一个(2,2)-型代数.若(S,+,·)满足:
(i) (S,+)和(S,·)都是半群,
(ii) (S,+,·)满足等式x(y+z)≈xy+xz和(x+y)z≈xz+yz,
则称(S,+,·)是半环.进一步,如果(S,+)是一个半格,则称(S,+,·)为ai-半环.在ai-半环(S,+,·)上,可以自然地引入偏序关系≤:
a≤b⟺a+b=b.
一个典型的ai-半环是半格的自同态半环.事实上,每一个ai-半环都可以嵌入到某一个半格的自同态半环中.众所周知,所有的ai-半环形成一个簇.近年来,关于ai-半环特别是ai-半环簇的研究已经成为半环理论的一个研究热点,取得了一系列重要的研究成果[1-8].特别地,一些学者对某些ai-半环簇的自由对象进行了刻画,给出了由某些特定等式所确定的ai-半环簇的自由对象的模型[6-7,9].特别地,在文献[7]中,该文作者引入了如下的ai-半环簇的自由对象.
令S是一个半群.用P(S)和Pf(S)分别来表示S的所有子集的集合和所有非空子集的集合.在P(S)上定义运算:A+B=A∪B,AB={ab|a∈A,b∈B},则P(S)和Pf(S)在上述运算下形成ai-半环.事实上,若X+表示非空集合X上的一个自由半群,则Pf(X+) 是ai-半环簇中相对于映射k:X→Pf(X+),x→{x}的自由对象.
设Sg(m,2,1)表示由附加恒等式(x1x2…xm)2≈x1x2…xm定义的半群簇,Sr(m,2,1)表示由附加恒等式(x1x2…xm)2≈x1x2…xm定义的ai-半环簇.近年来,一些学者对Sg(m,2,1)和Sr(m,2,1)进行了研究.例如,2002年,Ren等[6]利用半群的闭子半群给出了Sr(1,2,1) 中自由对象的模型.2005年,Pastijn等[2,5]证明了Sr(1,2,1)的所有子簇形成一个78阶的分配格,并且证明了这个簇的每一个子簇都是有限基底和有限生成的.
本文中引入半群的(m,2,1)-闭子半群的概念,并利用Sg(m,2,1)的自由对象来构造Sr(m,2,1)的自由对象.其结果将推广和丰富文献[6-7]中的结果.以下,用[n]表示集合{1,2,…,n}.其他概念和术语,读者可参考文献[10-12].
2 Sr(m,2,1)的自由对象
令S是一个半群,M⊆S,称M为S的(m,2,1)-闭子集,如果
pai11ai22…aimmq∈M(∀p,q∈S1,ai11,…,aimm∈S,i1,…,im=1,2)⟹pb11b12…b1mb21b22…b2mq∈M(∀bs∈{ai|∀∈[m]},s=1,2,∈[m]).
特别地,当m=1时,M即为文献[6]中引入的闭子集:称M是S的闭子集,如果对任意的p,q∈S1,a1,a2∈S,pa1q,pa2q∈M⟹pa1a2q∈M.显然,M是闭子集当且仅当M是(1,2,1)-闭子集.设A是半群S的一个子集.容易验证,S的所有包含A的(m,2,1)-闭子集(至少,S是一个包含A的闭子集)的交集仍然是S的一个(m,2,1)-闭子集并且是包含A的S的最小的(m,2,1)-闭子集.本文中称其为由A生成的S的(m,2,1)-闭子集,记作[A].如果A是一个有限子集,则称[A]是有限生成的.
引理1令S是一个半群且A是其子集.定义A(k)(k≥0)如下:
1)A(0)=A;
2)A(k+1)={pb11b12…b1mb21b22…b2mq|p,q∈S1,ai1,ai2,…,aim∈S,i1,…,im=1,2,pai1ai2…aimq∈A(k),bs∈{ai|∀∈[m]},s=1,2,∈[m]}∪A(k).
则对任意的A,B∈P(S),有
(i)A(0)⊆A(1)⊆…⊆A(k)⊆A(k+1)⊆…;
(ii)A⊆B⟹(∀k≥0)A(k)⊆B(k);
证明(i) 是显然的.
(ii) 令A⊆B.当k=0时,显然有A(0)⊆B(0).假设k≥0且A(k)⊆B(k),证明A(k+1)⊆B(k+1).令x∈A(k+1),需要考虑下列两种情况:
1)x∈A(k).因为A(k)⊆B(k),有x∈B(k).由B(k)⊆B(k+1)可以推出x∈B(k+1).
2)x=pb11b12…b1mb21b22…b2mq,p,q∈S1,ai1,ai2,…,aim∈S,pai1ai2…aimq∈A(k),i1,…,im=1,2,bs∈{ai|∀∈[m]},s=1,2,∈[m].因为A(k)⊆B(k),有{pai1ai2…aimq|ai1,ai2,…,aim∈S,i1,…,im=1,2}⊆B(k),因此x=pb11b12…b1mb21b22…b2mq∈B(k+1).
从而证明了A(k+1)⊆B(k+1).由归纳法可知,对任意的k,都有A(k)⊆B(k).
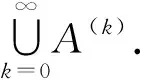
1)x∈A(k).因为A(k)⊆M,有x∈M.
2)x=pb11b12…b1mb21b22…b2mq,p,q∈S1,ai1,ai2,…,aim∈S,pai1ai2…aimq∈A(k),i1,…,im=1,2,bs∈{ai|∀∈[m]},s=1,2,∈[m].由A(k)⊆M,得到{pai1ai2…aimq|ai1,ai2,…,aim∈S,i1,…,im=1,2}⊆M.因为M是(m,2,1)-闭子集,从而可推出x=pb11b12…b1mb21b22…b2mq∈M.
引理2令S∈Sg(m,2,1),则对任意的k和A,B,C∈P(S),
A⊆B(k)⟹AC⊆(BC)(k),CA⊆(CB)(k).
证明由对偶原理,只需要证明对任意的k和A,B,C∈P(S),
A⊆B(k)⟹AC⊆(BC)(k).
当k=0时,如果A⊆B(0),则A⊆B.进一步,有AC⊆BC.从而推出AC⊆(BC)(0).假设k≥1且A⊆B(k).令a∈A,c∈C.因为a∈B(k),只需要考虑下列情况:
1)a∈B(k-1).由假设知ac∈(BC)(k-1),又由(BC)(k-1)⊆(BC)(k)可得ac∈(BC)(k).
2)a=pb11b12…b1mb21b22…b2mq,p,q∈S1,ai1,ai2,…,aim∈S,pai1ai2…aimq∈B(k-1),i1,…,im=1,2,bs∈{ai|∀∈[m]},s=1,2,∈[m].显然,{pai1ai2…aimq|ai1,ai2,…,aim∈S,i1,…,im=1,2}⊆B(k-1).由假设有{pai1ai2…aimqc|ai1,ai2,…,aim∈S,i1,…,im=1,2}⊆B(k-1),从而可以得到ac=pb11b12…b1mb21b22…b2mqc∈(BC)(k),因此有ac∈(BC)(k).从而有AC⊆(BC)(k).
由归纳法可知结论成立.
令S是一个半群.在Pf(S)定义二元关系ρ如下:
(A,B)∈ρ⟺[A]=[B].显然,ρ是Pf(S)上的一个等价关系.事实上,有
定理1令S∈Sg(m,2,1),则ρ是Pf(S)上的一个半环同余且Pf(S)/ρ∈Sr(m,2,1).
证明令A,B,C∈Pf(S)且(A,B)∈ρ.要证明ρ是一个半环同余,只需证明(A∪C,B∪C)∈ρ,(AC,BC)∈ρ和(CA,CB)∈ρ.
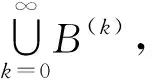
要证Pf(S)/ρ∈Sr(m,2,1),只需证A1,…,Am∈Pf(S),((A1…Am)2,A1…Am)∈ρ,即,[(A1…Am)2]=[A1…Am].令bi∈Ai,这里i∈[m],则b1…bm=(b1…bm)2∈(A1…Am)2.因此A1…Am⊆(A1…Am)2,进一步有[A1…Am]⊆[(A1…Am)2].如果x∈(A1…Am)2,则存在ai1ai2…aim∈A1…Am,ai1,ai2,…,aim∈S,i1,…,im=1,2,bs∈{ai|∀∈[m]},s=1,2,∈[m]使得x=pb11b12…b1mb21b22…b2mq.因为pb11b12…b1mb21b22…b2mq∈(A1…Am)(1)⊆[A1…Am],所以x=pb11b12…b1mb21b22…b2mq∈[A1…Am].因此(A1…Am)2⊆[A1…Am]并且[(A1…Am)2]⊆[A1…Am].因此得到[(A1…Am)2]=[A1…Am].
引理3设(S,·)∈Sg(m,2,1),(T,+,·)∈Sr(m,2,1),令φ是由半群S到半环T的乘法导出半群上的一个半群同态,则对任意的自然数k及A,B∈Pf(S),有

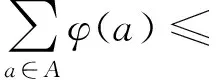
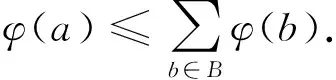
2)a=pb11b12…b1mb21b22…b2mq,p,q∈S1,ai11,ai22,…,aimm∈S,pai11ai22…aimmq∈B(k-1),i1,i2,…,im=1,2,bs∈{ai|∀∈[m]},s=1,2,∈[m].由归纳假设可得进一步,
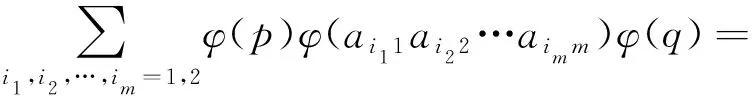
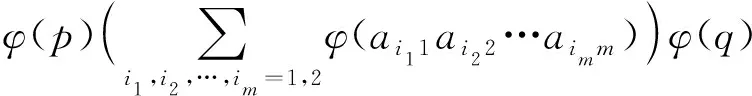
φ(p)(φ(a11)+φ(a21))(φ(a12)+
φ(a22))…(φ(a1m)+φ(a2m))φ(q)=
φ(p)((φ(a11)+φ(a21))(φ(a12)+
φ(a22))…(φ(a1m)+φ(a2m)))φ(q)≥
φ(pb11b12…b1mb21b22…b2mq)=φ(a).
上面是对于p,q∈S的情况的证明.p∉S或q∉S的情况可类似证明.
下面利用Sg(m,2,1)的自由对象来构造Sr(m,2,1)的自由对象.这一结果推广了文献[7]中的定理3.5.
定理2令X是一个非空子集,FX是X上Sg(m,2,1)相应于映射ι:X→FX的自由对象,则Pf(FX)/ρ是X上Sr(m,2,1)相应于映射κ:X→Pf(FX)/ρ,x→{ι(x)}ρ的自由对象.
证明由定理1可知Pf(FX)/ρ∈Sr(m,2,1).假设S∈Sr(m,2,1)且λ:X→S是任意一个映射.因为(S,·)∈Sg(m,2,1)且FX是Sg(m,2,1)的自由对象,则存在唯一的一个φ:FX→(S,·)使得

是一个交换图,即φ∘ι=λ.定义映射ψ:Pf(FX)/ρ→S如下:
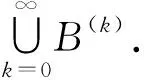

首先,对任意的A,B∈Pf(FX),
ψ((Aρ)+(Bρ))=
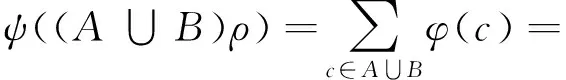
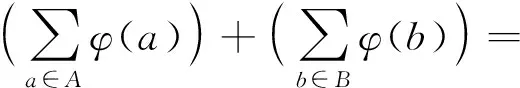
ψ(Aρ)+ψ(Bρ),
ψ((Aρ)(Bρ))=ψ((AB)ρ)=
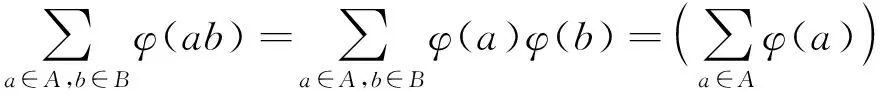
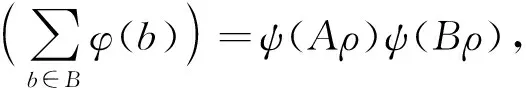
因此ψ是Pf(FX)到S上的半环同态.
其次,对任意的x∈X,(ψ∘κ)(x)=ψ(k(x))=ψ({ι(x)}ρ)=φ(ι(x))=(φ∘ι)(x)=λ(x),因而ψ∘κ=λ.
最后,令θ:Pf(FX)/ρ→S是一个半环同态且使得θ∘κ=λ,定义映射α:FX→(S,·)如下:
α(a)=θ({a}ρ)(a∈FX).
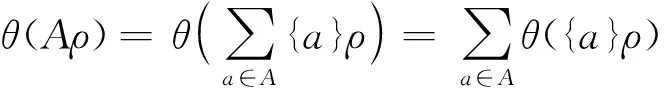
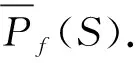
[A]+[B]=[A∪B],
[A]∘[B]=[AB](A,B∈Pf(S)).