转动Lambert圆锥激光后向散射Doppler谱的解析解
2018-10-09宫彦军王明军毕冬梅赵利军
宫彦军, 王明军, 毕冬梅, 赵利军
(1. 湖南科技学院 电子与信息工程学院, 湖南 永州 425199;2. 西安理工大学 自动化与通信工程学院, 西安 710048; 3. 长春大学 理学院, 长春 130022)
激光Doppler测速计(LDV)在测量时采用不接触的方式, 与传统测量方法相比具有较大优势[1]. LDV可提供纵向速度分量[2], 并获得振动装置的速度信息[3-5], 可利用激光Doppler效应测量一个点的振动速度[6]. 激光测速仪可测量流动液体的局部速度[7], 利用激光Doppler研究目标的Doppler成像, 可检测并识别球和圆盘[8-12]. LDV可快速直接测量血液的绝对速度[13]. 将激光扩束照射绕轴转动的目标, 整个目标可近似视为平面波照射, 对于运动的目标, 采用外差法可测量激光Doppler展宽[14], Doppler展宽能反应转动目标的形状特征及振动特征[15]. 文献[16-18]给出了Lambert圆锥激光后向散射Doppler谱的数值解; 文献[19]给出了在轨圆锥激光后向散射Doppler谱. 在热原子系统中, 探测场和耦合场存在Doppler效应[20], 文献[21]利用激光Doppler效应进行了旋翼弦长探测. 文献[16]只给出了圆锥和圆柱的数值解, 文献[17]给出了凸回转体的数值解, 文献[18]给出了凸二次回转体的数值解, 结果表明, 数值解给出的计算结果与计算精度有关, 数值解能计算的目标种类较多, 可计算不同表面材料. 本文给出转动Lambert圆锥激光后向散射Doppler谱的解析解, 其中表面材料是Lambert的. 结果表明, 解析解的计算结果与计算精度无关, 且给出的精确计算结果可用来验证数值解.
1 转动Lambert圆锥激光后向散射Doppler谱解析解的数学表达式
转动目标的激光后向散射Doppler谱是转动目标的激光后向散射Doppler频移对应的功率. Lambert圆锥绕其中心轴以角速度ω转动, 转动方向如图1所示, 用波长为λ的平面波激光照射圆锥.

图1 模型所用坐标系中的圆锥Fig.1 Cone in coordinate system used for model
圆锥中心轴与激光入射方向间的夹角为γ, 称为视线角, 圆锥中心轴为z轴, 圆锥顶点为坐标原点, 圆锥顶点指向底面中心的方向为z轴正向,z轴正向单位矢量为Z, 激光入射方向反方向的单位矢量为e, 选x轴正向的单位矢量
这里Z与e不平行, 因此
|e×Z|>0.
将激光扩束照射到绕轴转动的Lambert圆锥上, 圆锥均被照射到. 对于特定各向同性的粗糙面, 表面任意面元的激光后向散射强度由激光入射方向的反方向与该面元法线(指向物体外面)夹角β确定, β是光线在入射点处的本地入射角. 目标上每个可照射面元的后向散射功率[17]为
ΔP(β,t)=Kfr(β)ΔAcos2β,
(1)
其中fr(β)为圆锥粗糙表面在后向上的双向反射分布函数, 对于凸体, 满足cosβ>0的面元为可照射面元, 激光入射方向反方向在目标坐标系下的单位方向矢量e=(0,sinγ,-cosγ), 侧面上任意一点的单位法向量
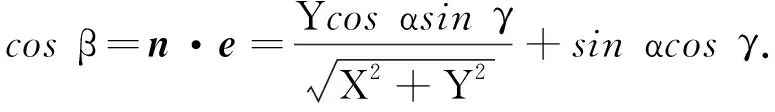
(2)
圆锥表面上任意可照射面元中心点的位置矢量r=(X,Y,Z), 角速度矢量Ω=(0,0,ω), 线速度矢量v=Ω×r=(-Yω,Xω,0). 在后向方向上的Doppler频移为
则
(3)

(4)

(5)
由式(3)可见, 对于圆锥表面X分量相同的点, 其Doppler频移一致, 为计算给定Doppler频移下的功率, 将式(5)在圆锥表面上可照射区域对Y积分, 则激光后向散射功率为
(6)
其中C为积分区域, 满足
(7)
由式(6)可得
(8)
由式(8)可得
(9)
其中

(11)
其中:
(12)
Y1=0,Y2=G2,γ=90°;
(13)

(14)
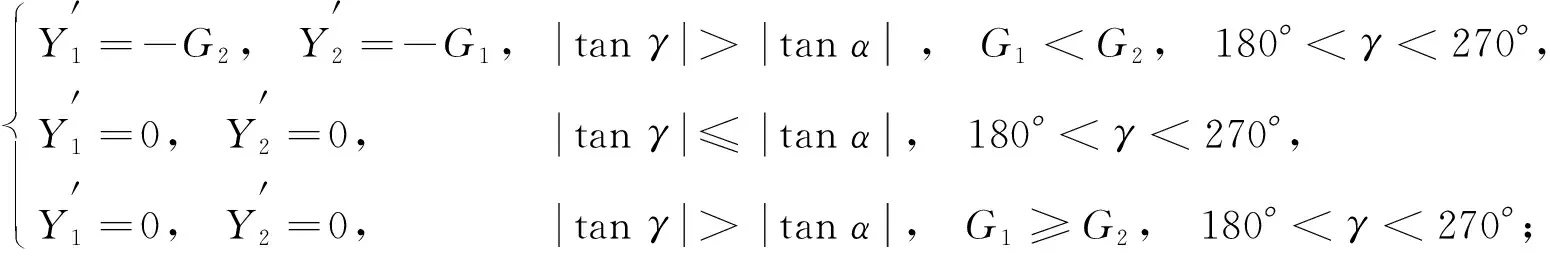
(15)

(16)
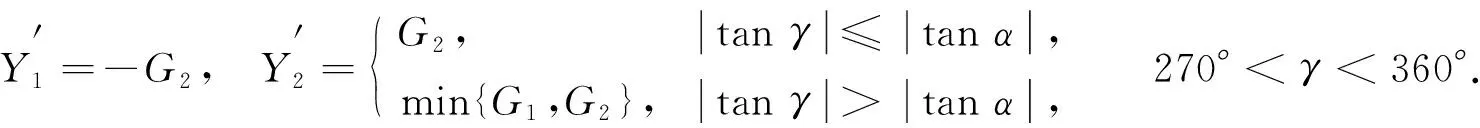
(17)

2 结果与讨论
圆锥具有对称性, 由于视线角γ和2π-γ关于z轴对称, 因此这两个视线角的Doppler谱相等. 下面给出证明. 假设0<γ<π, 根据式(10), 可得
根据式(18)、 式(19)和式(9)可得
下面将解析解和数值解进行对比, 其中圆锥的高度h=1 m, 半锥角α=5.7°, 角速度ω=1 rad/s, 波长λ=1 μm, Δx=5 mm,D=1,P(X,γ)为归一化功率. 图2为本文解析解与文献[17]数值解的比较, 其中: 图2(A)和(C)分别为视线角γ=10°,30°的解析解和计算精度Δy=20 mm的数值解; 图2(B)和(D)分别为视线角γ=10°,30°的解析解以及计算精度Δy=0.2,2 mm的数值解. 由图2(A)和(C)可见, 数值解和解析解的差异明显; 由图2(B)和(D)可见, 数值解和解析解的差异较小.

图2 解析解和数值解的比较Fig.2 Comparison of analytical solutions and numerical solutions
为显示数值解和解析解的差异, 本文给出不同精度数值解的误差, 结果如图3所示. 其中: 图3(A)和(C)分别为视线角γ=10°,30°的计算精度Δy=2,20 mm的数值解和解析解的差值; 图3(B)和(D)分别为视线角γ=10°,30°的计算精度Δy=0.2,2 mm的数值解和解析解的差值. 由图3可见, 随着计算精度的提高, 数值解和解析解的差值变小, 表明本文推导的解析解正确, 是Lambert圆锥激光后向散射Doppler谱的解析解, 数值解计算精度越高, 二者误差越小, 即解析解可确定数值解采用多大的计算精度能满足要求.

图3 不同计算精度数值解的误差Fig.3 Error of numerical solutions of different calculation accuracy
综上, 本文在本地坐标系下推导了Lambert圆锥激光后向散射Doppler谱的解析解, 并根据解析解的数学表达式证明了Lambert圆锥激光后向散射Doppler谱对于激光入射方向具有对称性, 即和为2π的两个视线角的Lambert圆锥激光后向散射Doppler谱相同. Lambert圆锥激光后向散射Doppler谱的数值解和解析解进行对比的结果表明, 随着数值解计算精度的提高, 数值解和解析解的误差变小.
