基于SPH-FEM耦合法的含缺陷输气管道爆炸冲击响应研究*

2018-10-09田晓建姚安林徐涛龙蒋宏业李又绿

中国安全生产科学技术 2018年9期

田晓建，姚安林,2，徐涛龙，蒋宏业，李又绿

(1.西南石油大学石油与天然气工程学院，四川成都 610500； 2.油气消防四川省重点实验室，四川成都 610500)

0 引言

油气管道的建设过程中，由于受各种影响因素的制约，多条管道并行敷设逐渐增多[1]。在一些地区因规划或集约化用地而往往要求尽量减小并行管道的间距[2]。加之城乡建设发展较快，管道多处占压，地区等级升级的情况越来越多，对在役管道的安全提出了挑战[3]，管道一旦发生爆炸或燃烧等事故，在冲击波或热辐射的作用下必将影响相邻管道的安全。因此，开展管道在爆炸荷载下的动力响应方面的研究显得尤为重要。

国内外学者开展了相关的研究工作并取得了一定成果。Parviz等[4]采用数值模拟的方法研究了爆炸荷载下土质、管材、TNT当量等对管道动力响应的影响，发现低密度土壤中的爆炸对管道的破坏较小；Adibi等[5]研究了爆破强度、管材厚度、埋深、混凝土保护层对管材变形的影响，结果表明埋深的增加使管道的变形减小；Vivek等[6]利用激波管产生冲击波进行室内模拟球形爆炸对管道的影响，结果表明管道受到冲击波的冲击立刻发生变形，压力阻尼随深度增加而增大；Mokhtari等[7]建立了基于欧拉-拉格朗日耦合法的三维有限元模型，分析了爆炸荷载下埋地管道的扰动(变形)行为；文霞等[8]基于ALE方法建立了隧道并行输气管道爆炸模型，分析不同工况下邻管对爆炸冲击的动力学响应；王德国[9]基于数值模拟的方法计算不同并行间距下架空天然气管道受并行管线爆炸冲击的超压及变形量。

已有研究均假定管道本体完好，缺乏对于含内腐蚀缺陷管道的动力响应研究。鉴于此，研究假定并行管道中的一条发生物理爆破，基于爆能相等原则确定TNT当量，在验证模型可行性的基础上建立基于SPH-FEM的管土-炸药耦合模型，重点分析了爆炸荷载下缺陷参数和爆心距对管道动力响应的影响，基于弹塑性失效准则求得管道安全平稳运行的临界深度和极限距离。研究可为埋地输气管道极端灾害下的风险评估提供技术支撑，为并行管道可能的抗爆隔爆设计提供模拟数据支持。

1 爆炸能量与TNT当量换算

1.1 物理性爆炸能量估算

压力容器因本构缺陷或压缩气体超压引发物理爆炸时，气体在容器破裂之前不会产生物态变化，只有简单的降温膨胀过程。容器内气体绝热膨胀所做的功转变为高温气体的爆炸能量，假定容器内气体的起始状态参数为(P0，V0)，经过绝热膨胀后其状态参数为(Pa,Va)，根据绝热方程PVk=C得到P0V0k=PaVak,则气体膨胀所做的功为:

(1)

若气体绝热膨胀所做的功全部转化为爆破释放的能量，则容器内压缩气体的爆破能量可以表示为：

(2)

式中：E为容器内压缩气体的爆破能量，kJ；P为容器内气体的绝对压力，MPa；V为容器的体积，m3；k为气体的绝热指数,取值范围为1.2～1.4，燃气一般取为1.29[10]。

1.2 等效TNT当量换算

当前TNT当量的换算方法主要有基于超压、基于爆热的等效计算方法和蒸汽云爆炸的当量计算方法。研究采用基于超压模型的等效TNT当量方法，计算公式[11]：

(3)

式中：WTNT为TNT当量，kg；E为超压爆炸能量，kJ；QTNT为TNT的爆炸热，取值范围为4 230～4 836 kJ/kg,通常取4.52×103kJ/kg。

2 数值模拟

2.1 物理模型建立及有限元网格划分

运行管线某段发生物理爆炸时，非爆破段管输介质对爆破段介质的膨胀做功有一定的干涉效应，忽略干涉效应仅考虑爆破段介质的做功可能与实际不符，但是目前对于干涉效应的研究尚缺乏相应的实验验证。所以，为了开展后续工作，笔者采用已有研究[12-14]所作的简化处理，取φ1 016 mm×26.2 mm，输送压力为10 MPa的爆管长度15.6 m，由式(2)求得爆破能量为280 646.387 4 kJ，由式(3)求得等效TNT当量为62.089 9 kg。由于结构的对称性，利用对称条件，建立如图 1所示的1/4物理模型，为方便建模炸药量取16 kg，药包尺寸为0.17 m × 0.34 m ×0.17 m，土体尺寸为8 m×6 m×6 m。炸药及炸药周围大变形区域采用SPH粒子，其余部分采用8节点六面体实体单元，为提高计算精度，在炸药、管道和炸药周围大变形区域细化网格边长至50 mm，缺陷网格为5 mm，远离爆炸近区单元边长过渡至500 mm。在模型对称面施加对称约束，底面和其余两侧面施加无反射边界约束，顶面为自由表面。

图1 物理模型及网格划分Fig.1 The physical model and grid partition

图2为含内点蚀缺陷管道示意图，A点为迎爆面正对爆心缺陷中心处，固定ai，bi(ai=bi)变化ci来改变缺陷的深度；固定ci变化ai，bi(ai=bi)来改变缺陷的表面尺寸；固定ai，bi和ci，移动缺陷到B，C，D和E点来改变缺陷的位置；固定ai，bi(ai=bi)和ci变化图 1 中的R来改变爆心距离。由此开展多工况下的算例分析。

图2 缺陷管道示意Fig.2 Schematic diagram of defective pipe

2.2 管道本构模型

材料本构采用MAT_PLASTIC_KINEMATIC模型。该模型遵从Von-Mises屈服准则，对于爆炸冲击荷载作用下的金属材料较为适用，利用其得出的结果与实验数据吻合较好[14]，因而被广泛应用。其本构方程为：

(4)

表1 管道的材料参数值Table 1 Material parameter value of pipe

2.3 土壤本构模型

土体本构选用带有失效准则的MAT_SOIL_AND_FOAM砂土模型，其理想塑性屈服函数为：

(5)

式中：Sij为偏应力分量；p为压力，MPa；a0，a1和a2为剪切屈服面常数。主要参数值：密度为1.8 g/cm3，剪切模量为63.8 MPa，体积卸载模量为30 GPa，拉伸截止值为-6.9 kPa，剪切屈服面参数a0=3.4×109Pa2，a1=7.033×104MPa，a2=0.3。其他材料参数[17]见表2。

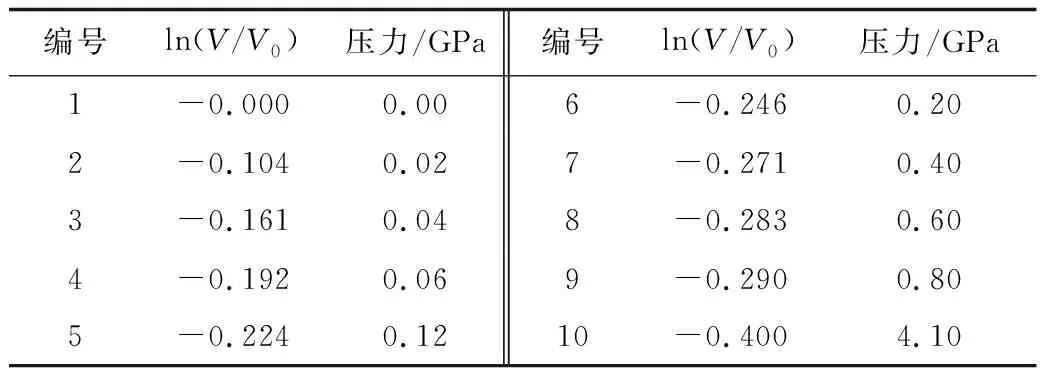
表2 砂土状态方程参数Table 2 Parameters of state equation of sand

2.4 炸药本构模型

炸药采用高能引爆燃烧材料模型MAT_HIGH_EXPLOSIVE_BURN和JWL状态方程：

(6)

式中：p为压力，MPa；E0为单位体积爆轰产物的内能，GJ/m3；V为爆轰产物的相对体积；A，B，R1，R2和ω为定值。炸药材料参数[18-19]取值见表3。

表3 炸药材料参数Table 3 Parameters of TNT charge

3 含缺陷管道动力响应结果分析

3.1 模型可靠性验证

为验证SPH-FEM耦合算法的可靠性，分别建立装药0.2 kg，药包埋深0.8，0.9和1 m的验证模型，研究土体爆炸空腔的变化发展规律。图3为爆腔模拟尺寸与穆朝民等[20]提出的爆腔预估公式计算值对比曲线图，包含了不同药包埋深下的最终爆腔形态，两者吻合较好，爆腔水平半径R2和装药上方半径R3均随药包埋深的增加而减小，前者减速平缓后者减速急剧；验证模型中地表面形成鼓包而无可见弹坑，随药包埋深的增加鼓包隆起度减小，爆腔内壁出现贯穿裂纹，爆腔由“倒梨形”向“椭圆形”过度。

图3 爆腔尺寸与药包埋深的关系Fig.3 The relationship between the size of brust cavity and the depth of TNT charge

土壤质点的峰值振速可由萨道夫斯基峰值振速经验公式[21]计算：

(7)

两端取对数：

(8)

式中，V为峰值振速，m/s；K为场地系数；W为装药量，kg；R为爆心距，m；η为衰减系数。

在验证模型中提取不同距离下土壤质点的峰值振速，分别进行函数拟合，拟合曲线如图4所示。公式中场地系数和衰减系数均接近，拟合曲线呈线性关系，与经验公式规律吻合，验证了SPH-FEM耦合法的可靠性。

图4 土壤质点峰值振速拟合曲线Fig.4 Fitting curve of peak velocity of soil particle

3.2 缺陷深度

为研究缺陷深度对管道动力响应的影响，在R=4 m时，设定图2中缺陷尺寸ai=bi=4 cm，缺陷深度ci由0.1t等距增至0.7t共4种设计工况，进行算例分析。

图5为不同工况下缺陷中心横截面上峰值位移分布。由图5可知，缺陷中心横截面上的峰值位移随ci的增大而增大，增速由缓慢到急剧，最大位移位于临近管道的顶部，这是由于随着时间的推移，爆炸空腔由“圆形”向“倒梨形”过度，爆腔形心上移，水平半径持续增大，因管体挤压管顶明显上移。

图5 缺陷中心管道截面上位移峰值分布Fig.5 Distribution of peak displacement on the cross section of a defect center pipe

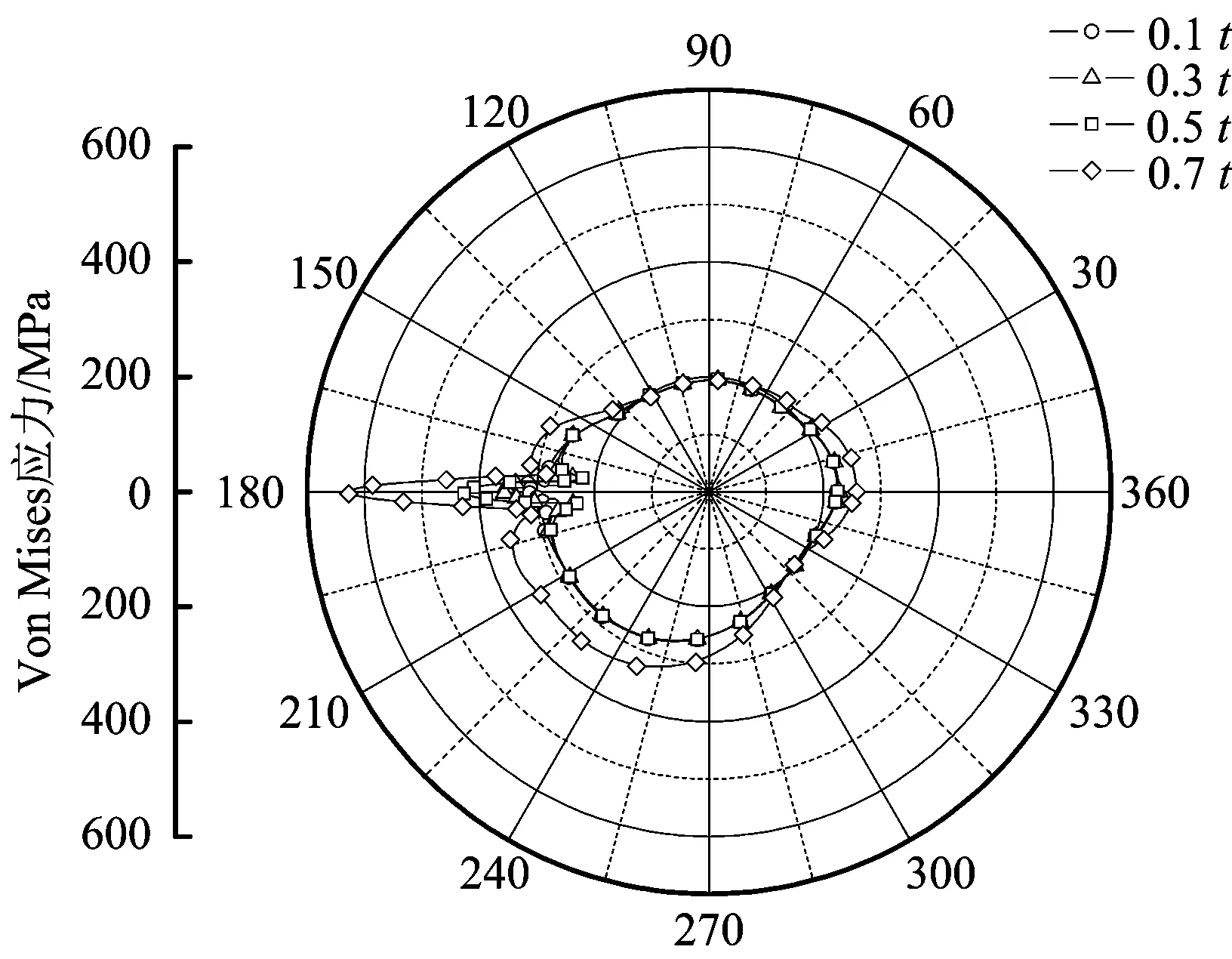
图6 缺陷中心管道截面峰值应力分布Fig.6 Peak stress distribution diagram of the cross section of a defect center pipe

图6为不同工况下缺陷中心横截面上峰值应力分布。由图6可知，截面上各处应力分布不均匀，缺陷处存在明显的应力集中现象，在缺陷边界处应力呈现先减小后增加的现象。随着缺陷深度的增加，横截面上各处应力呈增大趋势，缺陷中心峰值应力增速最快、应力最大，最大应力分别为315.26，355.61，426.18和626.46 MPa。横截面上各处应力分布沿水平线非对称，邻近爆心水平线下方120°范围内管体应力峰值大于水平线上方相同角度范围内的应力值，且ci越大，这种现象越明显。这是由于随着时间的推移，爆轰产物急剧扩张迫使周围土壤粒子急剧压缩移动并形成爆腔的过程中，缺陷中心水平线以下爆炸能量全部用于压缩土壤粒子，而水平线上方爆炸能量除部分用于压缩土壤粒子外，还有部分转化为土壤粒子的机械能，土壤粒子透过地表自由面被抛向空中并形成鼓包，导致部分能量耗散，因此呈现应力分布沿水平线非对称的现象。

图7为不同工况下缺陷中心横截面上峰值振速分布。由图7可知，横截面上峰值振速分布呈“草莓”状，峰值振速分布沿水平线趋近对称，随缺陷深度的增加呈增加的趋势，缺陷中心处峰值振速最大。

图7 缺陷中心管道截面峰值振速分布Fig.7 Peak vibration velocity distribution map of the defect center pipe section

综合图6～7可知，缺陷中心横截面上的位移、应力、振速分布沿水平线呈非对称关系；随缺陷深度的增加，均呈现增加的趋势，增速呈现由平缓到急剧的转变；缺陷处为响应的热点区域，缺陷中心为危险点。为此，将缺陷中心单元在不同ci下的峰值应力进行拟合，拟合曲线如图8所示，应力随着ci的增加呈指数增加。拟合公式为：

(9)

式中：y为缺陷中心处的峰值应力，MPa；x为缺陷的深度，cm。为保证管道的安全运行，基于塑性失效准则，由公式(9)求得满足条件的临界腐蚀深度为1.659 96 cm，约为0.633 6倍的管道壁厚。

图8 峰值应力拟合曲线Fig.8 Peak stress fitting curve

3.3 不同缺陷表面积

为研究缺陷表面尺寸对管道的动力响应规律，在爆心距R=4 m时，设定图2中缺陷尺寸ci=0.3t，ai=bi由4 cm等距增至10 cm共4种设计工况进行分析。

图9为不同工况下缺陷中心横截面上位移峰值分布。由图9可知，缺陷中心截面上的位移随缺陷表面积的增加呈减小趋势，背爆面上一定角度范围内呈现先减小后增加再减小的波动，位移分布总体差异较小。

图9 缺陷中心管道截面上位移峰值分布Fig.9 Distribution of peak displacement on the cross section of a defect center pipe

图10为不同工况下缺陷中心横截面上峰值应力分布。由图10可知，随着缺陷表面尺寸的增大，应力集中范围增大，缺陷中心处应力有小幅度的增加，应力分别为355.79，359.89，360.64和366.29 MPa，缺陷外应力分布无显著变化。此外，水平线两侧管体截面应力分布非对称，水平线下方应力较上方大。

图10 缺陷中心管道截面峰值应力分布Fig.10 Peak stress distribution diagram of the cross section of a defect center pipe

图11为不同工况下缺陷中心横截面上峰值振速分布。由图11可知，缺陷中心管道截面上的峰值振速分布曲线呈“草莓”状，迎爆面上的振速值大于背爆面的振速,水平线下方峰值振速略大于水平线上方峰值振速，随ai=bi的增加，各处峰值振速无明显变化，缺陷中心处峰值振速最大，最大分别为2.437 2，2.489 7，2.482 6和2.487 5 m/s。

综合图10～11可知，缺陷表面尺寸对缺陷中心管体横截面上的位移分布、应力分布和峰值振速分布影响较小。

图11 缺陷中心管道截面峰值振速分布Fig.11 Peak vibration velocity distribution map of the defect center pipe section

3.4 不同缺陷位置

管道内腐蚀一般发生于管道下部壁面[22]，为研究缺陷位置对管道动力响应的影响，研究仅针对缺陷位于管道下半部的情况。R=4 m时，设定图2中缺陷尺寸ai=bi=40 mm，ci=0.3 t，在A，B，C，D，E中变化缺陷位置，分析管体的动力响应特征。

图12为不同缺陷位置处的位移峰值分布。由图12可知，不同缺陷位置处的位移分布曲线存在微小差异，位于同一水平高度的缺陷，迎爆面上缺陷的曲线值高于背爆面的值，这是由于不同缺陷位置处的爆心距不同。

图12 缺陷中心管道截面上位移峰值分布Fig.12 Distribution of peak displacement on the cross section of a defect center pipe

图13为不同缺陷位置处的峰值应力分布。由图13可知，缺陷处存在明显的应力集中现象，迎爆面上的应力集中程度较背爆面大，缺陷外各曲线基本重合，反映了缺陷位置对管道动力响应的响应影响较小。此外，应力集中最明显的位置并非位于迎爆面上A处，而是位于迎爆面上的B处，这是由于炸药中心上方能量部分转化土壤粒子的动能，粒子被抛向空中形成鼓包，而下方能量全部用于压缩土体，力最终作用于管道，因而出现B处应力集中程度大于A处的现象。

图13 缺陷中心管道截面峰值应力分布Fig.13 Peak stress distribution diagram of the cross section of a defect center pipe

图14为不同缺陷位置处的峰值振速分布。由图14可知，峰值振速分布曲线呈“草莓”状，缺陷位于A点时，峰值振速最大，其最大值为2.506 7 m/s；缺陷位于C，D，E处时，缺陷中心处的峰值振速近似相等，分别为2.440 7，2.433 3和2.445 3 m/s；位于B处时，峰值振速最小，其最小值为2.388 9 m/s。当缺陷位于背爆面上的E处时，缺陷中心处有最大振速，其最大值为1.784 8 m/s，小于迎爆面上的最小振速2.388 9 m/s。

图14 缺陷中心管道截面峰值振速分布Fig.14 Peak vibration velocity distribution map of the defect center pipe section

综合图12～14可知，缺陷位置对管道的动力响应影响较小，迎爆面上的动力响应程度明显高于背爆面。

3.5 不同爆心距

为了定量研究管道的安全间距，基于后果最严重原则，研究ai=bi=40 mm，ci=0.7 t，R由4 m等距增至5.2 m共4种设计工况下管体的动力响应特征。

图15为不同工况下缺陷中心横截面上位移峰值分布。由图15可知，随着R的增大，缺陷中心横截面上的位移值减小，迎爆面上临近管顶处峰值位移最大，4种工况下最大位移分别为6.583 4，3.943 2，3.693 1和3.365 9 cm。

图16为不同工况下的峰值应力分布。由图16可知，缺陷中心横截面上的峰值应力分布呈“滴管”状，随着R的增大，应力分布值减小。缺陷处存在应力集中现象，且R越小应力集中现象越明显，且缺陷中心处应力峰值最大，4种工况下的应力峰值分别为473.27，504.54，516.58和627.32 MPa。截面上各点的应力分布关于水平线非对称，近爆点管体水平线下方120°范围内等效应力大于上方相同范围内的应力，背爆面水平线上方35°范围内应力大于水平线下方同等范围内的应力。

图17为不同工况下的峰值振速分布。由图17可知，缺陷中心横截面上的峰值振速分布呈“草莓”状，水平线下方曲线值略大于水平线上方曲线值，振速分布关于水平线近似对称。随着R的增大，峰值振速减小，减速由急剧到平缓。缺陷中心处的峰值振速最大，4种工况下最大振速分别为1.174 6，1.478 0，1.869 8和3.534 7 m/s。