考虑工程设施约束的海上油田群产液结构优化模型及其应用*

2018-10-09王守磊安桂荣耿站立

中国海上油气 2018年5期

王守磊安桂荣耿站立张伟

(1. 中国地质大学(北京) 北京 100083； 2. 中海油研究总院有限责任公司北京 100028)

区域联合开发是海上油田群一种重要的开发模式[1-3]，已广泛应用于南海油田群的开发。南海油田群主要为海相沉积，天然能量充足，单井产液量高，进入高含水期后需要提高单井产液量维持油田群稳产，而油田群的工程设施能力有限，不能满足所有油井的提液要求，同时工程设施扩容改造成本大，因此，需要在现有工程设施约束下合理分配油井产液量，优化油田群产液结构，从而实现油田群的高效开发。目前产液结构优化研究中多以考虑地质油藏因素为主，涉及工程设施约束较少[4-5]。虽有部分学者对考虑工程设施约束情况下的产液结构优化进行了研究，但局限于单个时间步内的优化，限制了矿场实际应用[6-8]。

本文考虑各个平台及整个油田群生产设施处理和外输能力，建立了海上油田群产液结构优化模型，通过增广拉格朗日函数法和G-SPSA算法，实现了海上油田群产液结构优化模型求解，并在实际油田群矿场应用中取得了良好效果。

1 海上油田群产液结构优化模型建立

1.1 单井开发指标预测

产液结构优化过程中根据单井的产油量和产水量等数据计算目标函数值，所以产液结构优化的关键问题是单井开发指标预测。单井开发指标预测方法主要有油藏工程方法和油藏数值模拟方法，其中油藏工程方法因操作简单、计算效率高而被广泛应用。水驱特征曲线是一种常用的预测开发指标的油藏工程方法[9-12]，张金庆提出的广适水驱特征曲线能够表征各种类型油藏含水率上升规律，适用于油藏开发的全过程[13-14]。本文采用广适水驱特征曲线对单井开发指标进行预测，其表达式为

(1)

式(1)中：Np为累积产油量，104m3；Wp为累积产水量，104m3；a、q和NR为广适水驱特征曲线参数，通过拟合历史生产数据可以得到。

单井开发指标预测主要分为两步：①选取具有代表性的历史生产数据，确定广适水驱特征曲线；②基于广适水驱特征曲线，预测不同时间步的产油量和产水量。这里主要介绍第2步的方法原理。

1) 给定一个累产油量增量ΔNp，则此时的累积产油量为

Np=Np0+ΔNp

(2)

2) 利用下式计算对应的累积产水量：

(3)

得到相应的累积产水量增量ΔWp为

ΔWp=Wp-Wp0

(4)

3) 计算累积产液量增量ΔLp为

ΔLp=ΔNp+ΔWp

(5)

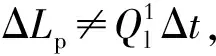
重复以上步骤即可得到不同油井在不同时间步的产油量和产水量。

1.2 产液结构优化模型建立

海上油田群产液结构优化就是在给定的调控时间步数内，在平台处理和外输能力一定的情况下，通过优化调整各油井的产液量，使得油藏的累积产油量或者净现值最大化。以净现值(NPV)最大化作为优化目标函数，即

MaximizeJ(u)=

(6)

1.3 约束条件

海上油田群采用区域联合开发时，油井产出液经过自身平台的外输管线先输送到中心平台进行液处理，中心平台再将处理后的原油通过管线外输到陆地。由于生产设施能力的局限性，海上油田群开发时受到的约束条件包括以下几类。

1) 单井边界约束。

油田实际生产过程中，由于泵排量限制，单井的产液量受到一定的约束，这属于边界约束。

(7)

处理边界约束最常见的方法包括截断法和对数变换法，此次研究主要采用对数变换法。通过对数变换，可使边界约束优化问题转化为无约束优化问题，其变换公式为

(8)

式(8)中：xi为变换后控制变量。

求解过程中，优化方法每次迭代都是在变换后的对数域上进行。当计算目标函数时，需要将控制变量转换到原域，其变换公式为

(9)

2) 平台外输约束。

采油平台上油井产液量受外输管线约束，存在一定上限。对于任意一个平台上的油井，其产液量之和要小于平台的外输能力，即

(10)

3) 中心平台液处理约束。

采出液通过采油平台外输到中心平台，由于中心平台的液处理设施能力是有限的，因此所有油井的产液量之和要小于中心平台的液处理能力，即

(11)

第2类和第3类约束的实质是等式约束或者不等式约束，因此，海上油田群产液结构优化数学模型可以表示为

MaximizeJ(u)

(12)

s.t.

(13)

ei(u)=0i=1,2,…，Ne

(14)

ci(u)≤0i=1,2,…，Nc

(15)

式(14)～(15)中：ei(u)表示第i个等式约束；ci(u)表示第i个不等式约束；Ne为等式约束个数；Nc为不等式约束个数。

2 海上油田群产液结构优化模型求解

2.1 求解方法

由上述分析可知，当考虑工程设施约束时，海上油田群产液结构优化问题为约束优化问题。对于约束问题，其求解思路一般是先利用增广拉格朗日函数法转化为无约束问题，然后利用优化算法对无约束问题进行求解。增广拉格朗日函数法是求解约束问题的一种常用解法，其思路是将原约束优化问题转化为一系列无约束优化子问题，并以此一系列无约束优化子问题的解去逼近原约束优化问题的解[15-19]。

在增广拉格朗日函数法中，将等式约束、不等式约束作为惩罚项与目标函数结合在一起构造增广拉格朗日函数，其表达式为

L(u,λ,μ)=J(u)-

(16)

其中

(17)

式(16)、(17)中：μ是惩罚因子；λe,i和λc,j分别为第i个等式约束和第j个不等式约束的拉格朗日乘子。

当拉格朗日乘子和惩罚因子确定时，此时优化模型为

MaximizeL(u)

(18)

使用增广拉格朗日函数法进行求解时，主要分为外循环和内循环两个过程。外循环中主要根据约束违反情况来更新拉格朗日乘子和惩罚因子，从而确定增广拉格朗日函数；内循环中主要采用G-SPSA算法来最大化增广拉格朗日函数。

具体计算步骤如下：

1) 确定拉格朗日乘子、惩罚因子等相关参数初始值。外循环迭代步l=1。

2) 建立增广拉格朗日函数，进入内循环。利用G-SPSA算法最大化增广拉格朗日函数，直至满足如下收敛条件。

(19)

(20)

式(19)、(20)中：k为内循环迭代步数；ξ1和ξ2分别为内循环中目标函数和控制变量的收敛值。

3)根据约束违反变量cv和允许约束违反值ηl来更新拉格朗日乘子和惩罚因子。

约束违反变量cv表达式为

(21)

若cv≤ηl，则有

(22)

ηl+1=max{ηlmin[(μl)0.2,0.5],η*}

(24)

式(24)中：η*为最小允许约束违反值。

若cv>ηl，则有

μl+1=τμl=0.1μl

(25)

ηl+1=max{ηlmin[(μl)0.1,0.5],η*}

(26)

4) 比较约束违反变量cv和最小允许约束违反值η*。如果cv≤η*，则表示所得的最优解满足约束条件，算法停止；否则，外循环迭代步l=l+1，返回步骤2，重复以上求解过程。

在内循环中，采用G-SPSA算法来最大化增广拉格朗日函数。G-SPSA算法是一种无梯度优化算法，仅需对目标函数进行计算，不需要梯度的求解，已广泛应用于实际油藏问题中[20-23]。优化算法的本质就是确定新的搜索方向，生成新的控制变量，直到达到收敛条件,得到最优解。利用G-SPSA算法来确定新的搜索方向的具体步骤如下。

1) 采用球形模型产生协方差矩阵Cu。协方差矩阵中任一元素Cp,q为

(27)

式(27)中：p和q分别表示第p、q个调控时间步；σ代表标准差；t表示相关联的时间步数。

2) 生成M个随机控制变量uk,i，其表达式为

uk,i=uk+εkCu1/2Zk,ii=1,2,…，M

(28)

式(28)中：uk是内循环中第k步最优控制变量；εk是扰动步长；Cu1/2为Nu×Nu维下三角矩阵，通过对Cu进行Cholesky分解得到；Zk,i为服从高斯分布的扰动向量，Zk,i～N(0,I)，其中I是Nu×Nu维单位矩阵。

3) 计算搜索方向dk，其表达式为

(29)

其中

(30)

4) 生成新的控制变量uk+1,其表达式为

(31)

式(31)中：αk为搜索步长，可通过一维搜索方法来确定。

2.2 求解流程

图1 海上油田群产液结构优化计算流程

海上油田群产液结构优化模型的求解流程如图1所示,主要包括以下几个步骤：①首先根据单井历史生产动态，选取具有代表性的拟合段得到反映单井生产特征的水驱特征参数。②设定控制变量、惩罚因子和拉格朗日乘子的初始值，建立增广拉格朗日函数，开始外循环。③进入内循环，调用G-SPSA算法更新控制变量，根据控制变量，利用广适水驱特征曲线预测单井开发指标，从而计算拉格朗日函数值。④判断是否满足内循环收敛条件，满足收敛条件，则跳出内循环，进入外循环；否则，继续下一个内循环；⑤判断是否满足外循环收敛条件，满足收敛条件，则停止；否则，根据约束违反情况，更新惩罚因子和拉格朗日乘子，进入下一个外循环。

3 模型的应用

3.1 基本参数

以海上LP油田群为例进行产液结构优化。该油田群包括XA、XB、XC等3个油田，3个油田均处于特高含水阶段，对应有3座平台，其中PA和PB平台为采油平台，PC平台为中心处理平台。2个采油平台的采出液外输能力分别是10 000 m3/d和20 000 m3/d，中心平台的液处理能力为50 000 m3/d。该油田群储层以三角洲前缘的河口砂坝及三角洲平原的分流河道砂体为主，孔隙度为21.5%～31.5%，渗透率为1 256～6 043 mD，地层原油黏度为5.8～21.7 mPa·s，边底水能量充足，无注水井，3个油田的油井数分别是4口、7口和10口。每口油井每180 d调控一次，调控步数是6，总的调控时间是1 080 d。控制变量的个数是(4+7+10)×6=126。

优化过程中，原油价格为2 500元/m3，水处理费为55元/m3，折现率是12%。油井产液量的最小和最大值分别设定为1 000 m3/d和3 000 m3/d。油井初始产液量为目前生产过程中的实际产液量。

惩罚因子初始值由下式确定：

(32)

由于约束条件中没有等式约束，所以等式约束的拉格朗日乘子设置为零。不等式约束的拉格朗日乘子由下式确定：

初始允许约束违反值η(0)=0.1，最小允许约束违反值η*=0.1η(0)。内循环收敛条件中，分别设置ξ1=0.01和ξ2=0.01。优化算法G-SPSA生成随机扰动梯度的样本个数M=10。

3.2 优化结果

目前LP油田群中XA和XB平台上油井的产液量已分别达到9 000 m3/d和16 000 m3/d，接近平台外输能力，XC平台的液处理能力已达到上限50 000 m3/d。各油井按照目前产液量继续生产作为基础方案。

在保持平台外输和处理能力不变的情况下，利用本文提出的方法对LP油田群基础方案进行优化。优化结果显示，每个时间步内，XA和XB平台上的油井产液量小于外输能力约束，整个油田群的产液量小于XC平台液处理能力约束；在油田群相同产液量情况下，优化方案累产油174.9×104m3，较基础方案累产油(166.3×104m3)增幅5.2%。从经济效益来看，优化方案净现值为12.9亿元，较基础方案净现值(12.1亿元)增幅6.8%。

目前LP油田群中XA、XB、XC等3个平台的含水率依次增加。如表1所示，优化以后，XB和XC平台上的油井累积产液量有所下降，累积产油量有所上升，起到了稳油控水的效果；XA平台通过增加累积产液量，累积产油量也有所增加，起到了提液增油的效果。可见，优化方案通过降低高含水率平台产液量，增加低含水率平台产液量，改善了该油田群开发效果。

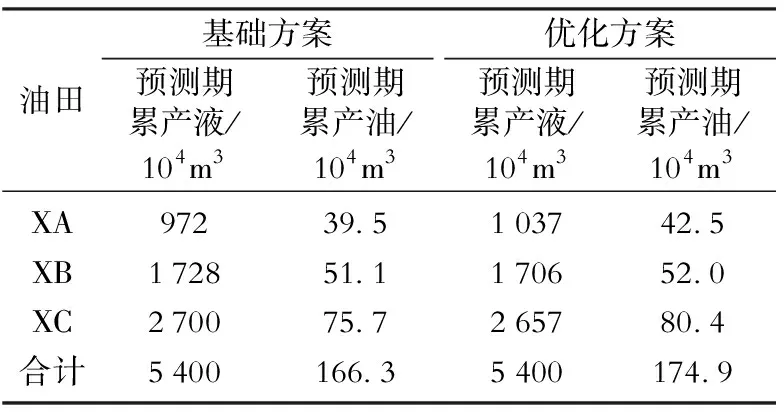
表1 海上LP油田群产液结构优化结果

以XA平台的4口井为例，目前XA-1、XA-2、XA-3、XA-4等4口井的含水率依次升高，因此，在平台外输能力有限的情况下，产液结构优化中应尽量提高含水率较低的油井液量，降低含水率较高的油井液量。从表2可以看出，优化后XA-3和XA-4井的液量都有所提高，产油量明显升高，而XA-2和XA-1井的液量有所降低。尽管这2口井的液量降低导致产油量降低，但从整体来看，整个平台的产油量得到了增加。可以说，在每个平台内部也起到了产液结构优化的效果。