解直角三角形的类型和应用

江西省赣州市南康区连城初中 曾凡廷

解直角三角形是空间与图形中的重点内容，它是根据直角三角形的性质和已知条件，计算直角三角形未知的边长、角度和面积以及相关的几何图形的数量，同时是解决实际生活问题中的重要数学模型。中考数学试题主要是考查学生对解直角三角形知识的理解以及解决实际生活问题的能力，在中考试题中占有较大的比例（约10%左右）。

一、解直角三角形的基本类型和方法

要解直角三角形，在给出的两个元素中（除直角外），至少有一个是边。解直角三角形可分为两大类，其一为已知一条边和一个锐角，其二为已知两条边。四种基本类型和解法列表如下：

?

此类题型在中考试题中主要是以填空题、选择题形式出现，重点考查特殊角的三角函数值及三角函数定义。

例1 如图1，在△ABC中，AC⊥BC，CD⊥AB，且∠A＝30°，AE＝2，则AB=___。

解析：所求是Rt△ABC的斜边，但在Rt△ABC中只知一个锐角A＝30°，暂不可解。先在Rt△ADE中，已知一直角边及一锐角可求得：AD=AE÷cos30°=2÷cos30°，然后在Rt△ACD中求出最后求出AB。

图1

说明：本题是由几个直角三角形组合而成的图形。对于这样的问题，先解出已经具备条件的直角三角形，从而逐步创造条件，使问题获得解。

例2 如图2，在Rt△ABC中，∠C＝90°，D为BC的中点,若，求AD的长。

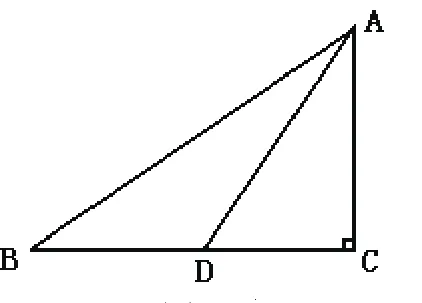
图2

说明：解直角三角形时，直角三角形中有关图形之间的数量关系，会呈现出许多不同的解直角三角形问题，应注意三角形中主要线段的性质，利用平面几何的有关定理，能够建立已知与未知的联系，然后找到解决问题的突破口。

二、解直角三角形在实际问题中的应用

此类题型在中考试题中主要是以解答题的形式出现，属中档题，重点考查由直角三角形中的有关知识来解决实际问题的应用能力和以三角函数为题设条件的三角型综合题。

利用解直角三角形的知识解决实际问题，主要包括度量工件、测量距离、工程技术等方面，而解决问题的关键是要从实际问题中抽象出几何图形，找出数学模型（解直角三角形），使实际问题得到解决。

例3 如图3，某勘测队要测一座山的高度，先在山脚（点B）测得山顶的仰角为36°，沿倾斜角为20°的山坡前进600米（点D），又测得山顶的仰角为60°，求山的高度（精确到0.1米，可用计算器）。

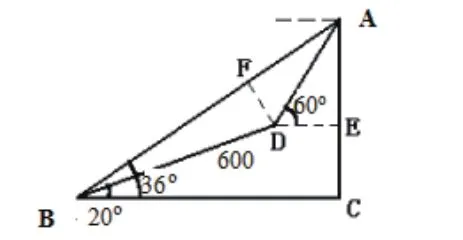
图3

分析：如图可知，AC为山高，BD为山坡，∠DBC＝20°，∠ABC＝36°（仰角为视线与水平线的夹角），BD＝600米，∠ADE＝60°，要直接在Rt△ABC中求BC条件不够，必须设法先求出AB，这就需要构造新的直角三角形。

解：过D作DF⊥AB于F，在Rt△BDF中，∠DBF＝36°-20°＝16°，

∴BF＝BD·cos∠DBF≈600×0.9613＝576.76（米），DF＝BD·sin∠DBF≈600×0.2756＝165.38（米）。

在Rt△ADF中，∵∠DAF＝60°-36°＝24°，∴AF＝DF÷tan∠DAF≈165.38÷0.4452＝371.44（米）。

∴AB＝AF＋BF＝371.44＋ 576.75＝948.19（米）。

在Rt△ABC中，AC＝AB·sin∠ABC≈948.19×0.5888＝557.3（米）。

答：山高为 557.3米。

说明：应用问题的题型千变万化，关键是转化为解直角三角形的数学模型，从而得解（必要时应添加适当的辅助线，构造出直角三角形）。

说明：

1.测量底部不可以到达的物体的高度的问题，通常是根据两个直角三角形的边长关系，列出含有被测物体高度的方程；

2.测量底部可以到达的物体的高度的问题，常采用如下模型和公式：如图4，已知CE＝a，CD＝b，∠ACE＝α，则AB＝AE＋b＝a·tanα＋b。

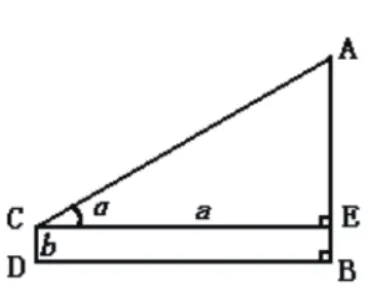
图4