有色Petri网在平交道口安全性分析中的应用
2018-10-09陈黎洁宋凤娟
孙 超,陈黎洁,宋凤娟
(1.中国铁道科学研究院集团有限公司 标准计量研究所,北京 100081;2.北京全路通信信号研究设计院集团有限公司,北京 100073)
随着铁路建设的发展以及道路交通工具数量的增长,平交道口(LC,Level crossing)存在很大的安全隐患[1]。平交道口一旦发生交通事故,不仅中断铁路运输,阻塞道路交通,还会引起严重的人员伤亡和财产损失[2]。形式化方法可以通过具有明确数学定义的文法和语义方法或语言对LC的期望特性和行为进行精确、简洁描述,得到其数学模型,通过计算方式对模型性质进行分析和验证,能够发现LC存在的风险,提高其安全性[3-4]。
相对于其他形式化语言,有色Petri网具有直观的图形表示和严密的数学基础,在描述系统的分叉、同步和并行等行为、层次化建模及处理数据方面具有很大优势[5],因为基于模型的分析方法能够直观体现系统的行为[6]。同时,有色Petri网支撑时序逻辑语言ASK-CTL的运行,ASK-CTL时序逻辑是一种形式化语言,其主要作用是进行计算的逻辑推理,通过时序连接词将时间建立成一系列“状态”序列,通过搜索模型中是否具有用ASK-CTL描述的状态来验证模型代表的系统是否符合需求[7]。文章用有色Petri网分析平交道口的安全性:(1)运用有色Petri网工具对平交道口建立模型;(2)用ASK-CTL语言表示平交道口的安全需求;(3)通过模型检验的方法进行功能验证。
1 有色Petri网方法
有色Petri网是在Petri网的基础上加上模块化的功能,使模型能够分成不同的模块,降低了每个模块中模型的复杂程度,其相关的变量参数定义如下:
(1)元素的类型用Type表示,变量v的类型用Type(v)表示;
(2)变量集合V的绑定,即每个变量v∈V与一个具体元素b(v)∈Type(v)相关联,元素b(v)是属于Type(v)类型的。
1.1 有色Petri网语法
1.2 ASK-CTL语法
ASK-CTL公式由路径量词、时态运算符和性质描述符3部分构成。路径量词包括A(对于所有路径)、E(存在某个路径);时态运算符包括 G(Global)、F(Future)、X(next)、U(Until);性质描述符用来描述系统模型的性质或状态,可以用a、b表示。
1.3 ASK-CTL语义
用S表示状态,那么有
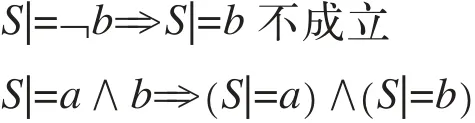
S|=EFb==>存在从状态S出发的路径满足Si|=b,i≥0
S|=AFb==>对所有从状态S出发的路径满足Si|=b,i≥0
S|=EGb==>存在从状态S出发的路径满足ASi|=b,i≥0
S|=AGb==>对所有从状态S出发的路径满足ASi|=b, i≥0
2 平交道口结构
本文选用单条轨道和双向道路组成的平交道口作为分析对象,包含道路警报灯、护栏、信号机、传感器、控制单元,如图1所示[8-9]。
平交道口系统的工作流程为[10]:(1)当列车接近道口传感器检测到有列车接近平交道口时,传感器将列车接近信息发送给控制单元;(2)控制单元向道路警报灯和护栏发出控制命令,道路警报灯闪烁,护栏落下,护栏向控制单元反馈护栏落下信息;(3)控制单元给轨旁信号机发送绿灯命令,将信号灯从红色转换为绿色,如果信号机未收到控制单元的绿灯命令,信号灯需保持红色。如果列车接近,但信号灯仍然为红色,列车必须停在信号机前。当列车到达平交道口并且被列车出清传感器检测到后,列车出清传感器向控制单元反馈列车已出清信息;(4)控制单元向信号机发送红灯命令,将信号灯置为红色,同时向道路警报灯发送熄灭命令,向护栏发送抬升命令。
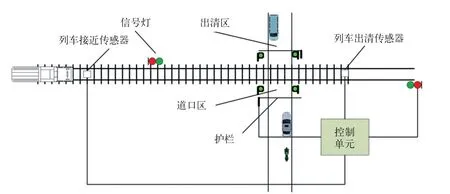
图1 平交道口结构
3 平交道口有色Petri网模型
基于有色Petri网的模块化功能,可以将平交道口的模型分为:轨道交通系统模型、道口控制系统模型和道路交通系统模型。CPN Tools是典型的有色Petri网建模工具,本文使用CPN Tools建立相关模型。
3.1 轨道交通系统有色Petri网模型
图2是平交道口的轨道交通系统模型。这里考虑客运和货运两种列车类型,变迁“Passenger train”和变迁“Freight train”的触发分别代表两种车型的选择。参考经验数据,客运列车出现的概率为0.8,货运列车出现的概率为0.2,库所“Train Approaching LC”中包含1到10之间随机分布的变量,用令牌E表示,当变量大于2时,表明以0.8的概率触发变迁“Passenger train”。同理,变量不大于2时,表明以0.2的概率触发变迁“Freight train”。
3.2 道口控制系统有色Petri网模型
道口控制系统的工作流程为:检测到有列车接近平交道口时,道路警报灯闪烁4 s,然后信号灯变成红色,护栏落下。直到检测到列车已出清平交道口,信号灯由红色变成绿色,同时护栏升起。道口控制系统具备“关闭”和“开启”两种状态,一旦信号灯为红色,平交道口对道路交通系统就是关闭的,同理,一旦列车出清平交道口并且信号灯变成绿色以后护栏完全升起,平交道口对道路交通系统就是开启的。
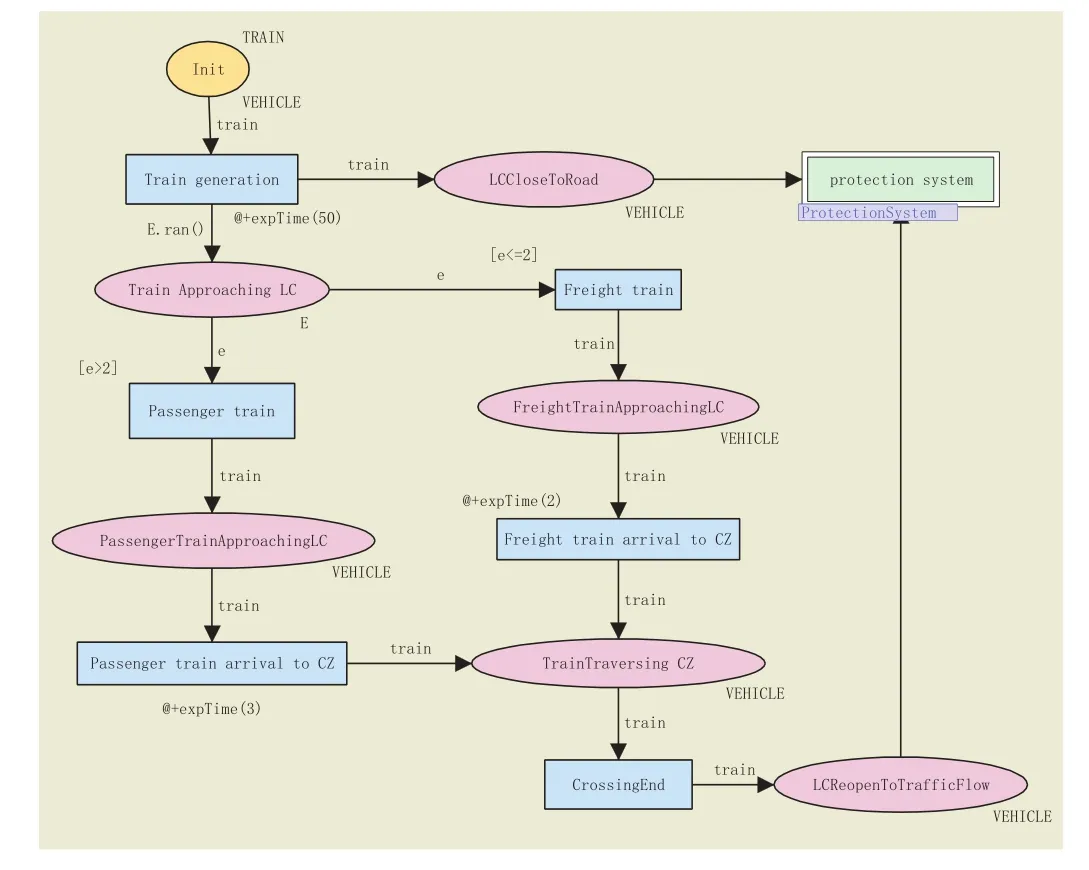
图2 轨道交通系统模型
图3表示道口控制系统的模型。初始情况下,平交道口对道路交通系统是开启的,这用库所“LCOpenToRoadTraffic”中包含一个令牌来表示。变迁“close”的触发代表信号灯变成红色并且护栏落下,其符号@+4代表该动作有4 s的延时,即列车接近平交道口时道路警报灯闪烁4 s以后。库所“LCCloseToRoadTraffic”代表平交道口处于关闭状态,库所“open”代表因为信号灯变成绿色并且护栏升起,平交道口重新开启。
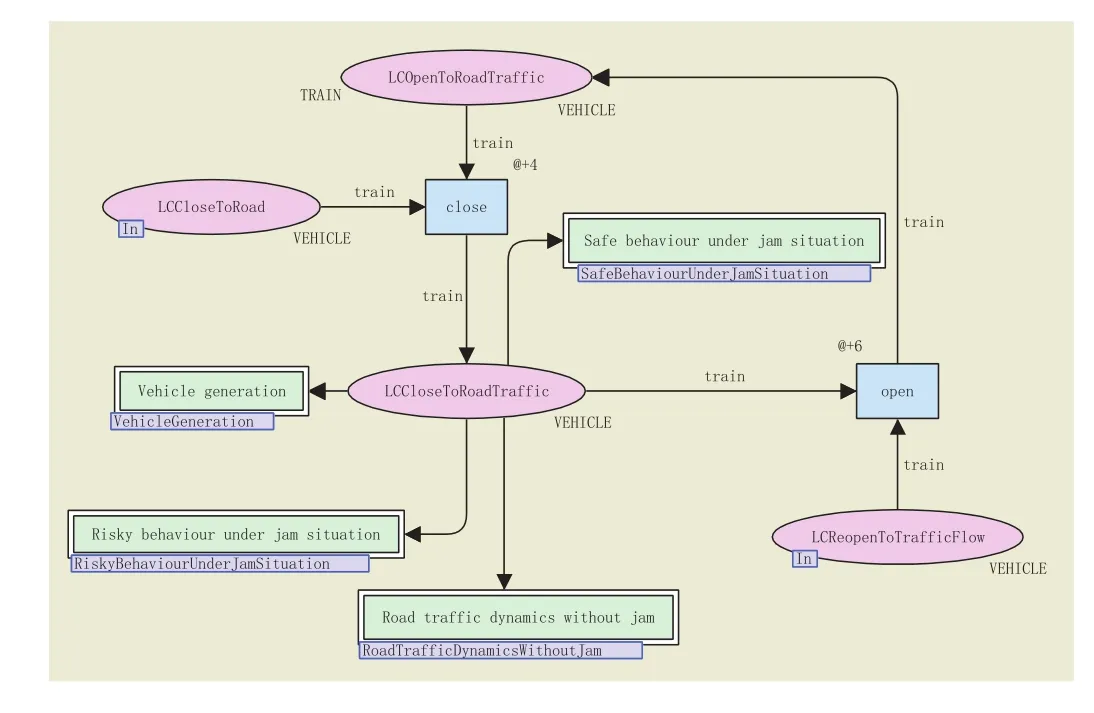
图3 道口控制系统模型
3.3 道路交通系统有色Petri网模型
在平交道口的出清区道路交通存在拥堵和无拥堵两种情况,而存在拥堵时,道路交通存在安全导向和风险导向两种情况,因此,道路交通系统的模型可以进一步划分为无拥堵时的道路交通系统模型、汽车驶入平交道口模型、有拥堵时道路交通系统的风险导向模型、有拥堵时道路交通系统的安全导向模型,如图4所示。表1总结了图4中各变迁代表的含义。
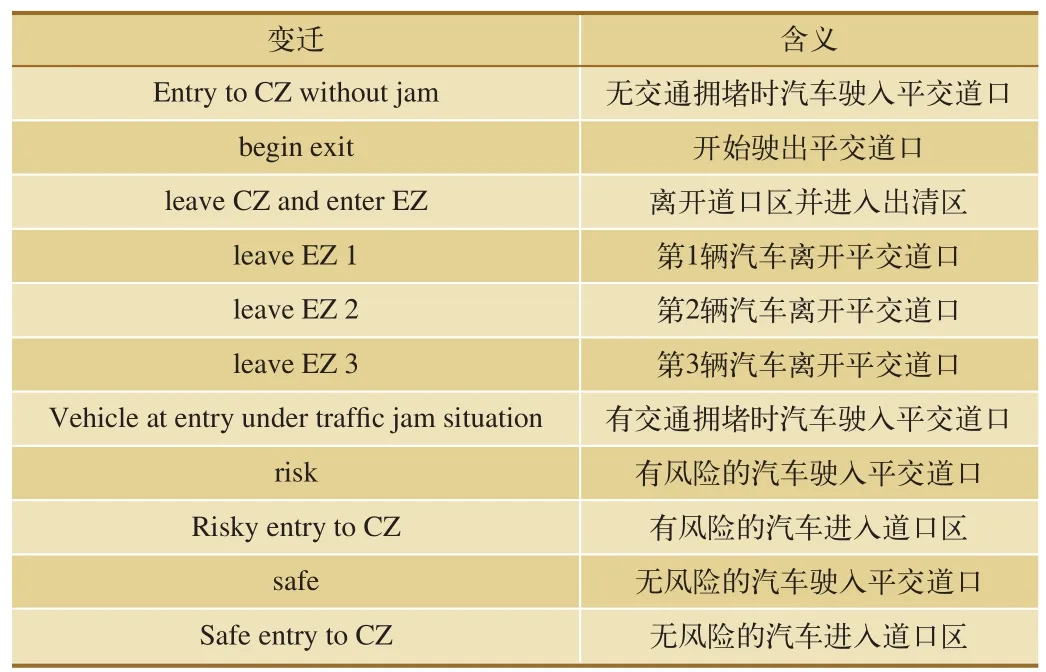
表1 道路交通系统模型中各变迁的含义
3.3.1 无拥堵时道路交通系统模型
无拥堵时的道路交通系统模型如图4a所示。库所“VehicleApproachingLC”表示在汽车靠近平交道口的出清区没有交通拥堵。用M(“”)表示库所中存在的令牌数量,无交通拥堵情况下,出清区最多只能同时存在两辆汽车,那么M(“VehiclesInCZ”)+ M(“AnotherVehiclesInCZ”)= M(“VehiclesStillInCZ”)+ M(“AnotherVehiclesStillInCZ”)= 1,即 库 所“VehiclesInCZ”和库所“AnotherVehiclesInCZ”中的令牌总数为1,同理,库所“VehiclesStillInCZ”和库所“AnotherVehiclesStillInCZ”中的令牌总数也为1。两辆汽车依次通过道口区的场景可以由库所“VehiclesInCZ”、库所“VehiclesStillInCZ”,以及变迁“Entry to CZ without jam”、变迁“begin exit”、变迁“leave CZ and enter EZ”共同描述。变迁“Entry to CZ without jam”表示汽车进入道口区,变迁“begin exit”表示开始离开道口区,变迁“leave CZ and enter EZ”表示完全离开道口区并进入出清区。
图4a中模型从变迁“leave CZ and enter EZ”开始往下的部分表示出清区的汽车的行为。库所“RemainingCapacity”表示出清区汽车的最大容量,本文假设出清区汽车的最大容量为3,库所“Counter”表示出清区剩余的汽车数量,那么有M(“Counter”)+ M(“Vehicle1RemainEZ”)+ M(“Vehicle2RemainEZ”)+ M(“Vehicle3RemainEZ”)= 3。库所“Counter”中的令牌数量到达3,变迁“Entry to CZ without jam”不能再触发,表示出清区汽车数量一旦到达其最大容量,汽车不再进入道口区。因此,一旦变迁“Entry to CZ without jam”触发,表明平交道口的汽车不会引起拥堵。
3.3.2 汽车驶入平交道口模型
汽车驶入平交道口的模型如图4b所示。变迁“Vehicle at entry under traffic jam situation”触发的条件之一是图4a模型中库所“RemainingCapacity”的令牌数为3,即出清区汽车数量到达最大容量,发生拥堵。此时可能发生两种情况:(1)汽车继续驶入道口区,触发图4c中模型的变迁“risk”;(2)汽车等在平交道口的入口直到出清区的汽车离开,触发图4d中模型的变迁“safe”。
3.3.3 有拥堵时道路交通系统风险导向模型
有拥堵时道路交通系统的风险导向模型如图4c所示。此时出清区已经发生拥堵,汽车继续驶入道口区是存在一定风险的。变迁“risk”的触发表明汽车驶入道口区。
3.3.4 有拥堵时道路交通系统安全导向模型
有拥堵时道路交通系统的风险导向模型如图4d所示。变迁“Safe entry to CZ”的触发条件之一是库所“Counter”中的令牌数小于3,即只要出清区的汽车数量不小于3,就没有汽车驶入道口区。


图4 道路交通系统模型
3.4 整体模型
有色Petri网能够通过模块化的方法根据平交道口的功能将其模型分解成不同的模块,为了体现各模块之间的关联性,本节描述图4各模型之间的关系。
3.4.1 轨道交通系统和道口控制系统之间的关联
一旦检测到列车接近平交道口,平交道口对道路交通系统关闭,该状态用图2模型中的库所“LCCloseToRoad”表示,同理,一旦列车离开道口区,平交道口对道路系统开启,该状态用图2模型中的库所“LCReopenToTrafficFlow”表示。这两个库所是图3中模型的变迁“close”和变迁“open”的触发条件。
3.4.2 道口控制系统和道路交通系统之间的关联
道口控制系统的任务是允许或禁止汽车通过平交道口,因此图4a模型中的变迁“Entry to CZ without jam”、图4b中模型的变迁“Vehicle at entry under traffic jam situation”、图4c中模型的变迁“Risky entry to CZ”、图4d中模型的变迁“Safe entry to CZ”的触发条件之一是图3中模型的库所“LCCloseToRoadTraffic”没有令牌。
4 平交道口模型分析与验证
模型检验是关于系统属性验证的算法和方法,基本思想是用状态迁移系统列举系统存在的所有状态,用时序逻辑公式描述系统的目标状态,通过状态空间查询的方法查找列举的系统状态中是否存在符合目标的状态。CPN Tools除了能够建立模型,还为时序逻辑公式ASK-CTL的运行提供了环境,本章使用CPN Tools对平交道口的模型进行检验。
4.1 安全性分析算法
系统安全性的定义为:系统不期望的状态永远不会发生,对应到模型中则是通过所有路径都能达到安全的状态。本文平交道口的安全性分析算法如表2所示。

表2 安全性分析算法
4.2 安全性分析过程及结果
根据表2的算法,表3给出了对平交道口安全性分析的过程及结果。
4.3 到达非安全状态的路径查找
从分析结果看出不是所有路径都能到达安全状态,即代表汽车的令牌可能不在道路交通系统安全导向模型中,存在非安全状态,那么就要查找到达非安全状态的路径。查找到达非安全状态路径的算法及路径如表4所示。

表3 平交道口安全性分析结果

表4 到达非安全状态的路径查找算法及路径
从到达非安全状态的路径中可以看出,是因为道路交通系统风险导向模型中变迁“risk”的触发导致代表汽车的令牌未进入道路交通系统安全导向模型中,引起了非安全状态的出现。这是因为在平交道口的出清区汽车数量已经达到最大容量时,汽车司机可能会等到出清区的汽车数量减少时再驶入平交道口,也可能会直接驶入平交道口。
5 结束语
铁路的建设发展进入一个全新的阶段,无论是列车的速度、密度还是列车的载重都比以前有了极大的提高,与此同时,公路运输量也在不断提高,道路交通工具数量大幅增长。这样的交通现状加上有待提高的人口素质,导致平交道口存在很大的安全隐患。因此,平交道口的安全性是当前交通运输行业亟需重视的问题。
本文将有色Petri网用于平交道口的安全分析中,相对于已往对平交道口安全性分析方法上研究的不足,该方法不仅能够描述平交道口的功能特征和动态行为,还能够对功能进行验证。利用有色Petri网对平交道口进行了形式化描述,针对平交道口中的轨道交通系统、道口控制系统和道路交通系统进行了建模,最后应用有色Petri网环境下的模型检验工具ASK-CTL进行了功能验证,验证结论表明了平交道口模型功能的正确性以及方法的可行性。
