债券收益率的模型研究

侯 蕾，黄汉江

（上海理工大学 管理学院，上海200093）

1 绪论

随着证券市场的发展，许多经济学家开始将研究的目光从股票市场转向债券市场，尤其是国债市场。国债体现了国度的信用，既是对一个国度经济水平的说明也是对一个国度公信力的程度说明。因此，研究国债市场和分析债券的收益，对推动中国债券市场的进步有着十分积极的影响[1]。

国外证券的发展时间较长，总体的市场以及投资比较成熟，因此国外的学者以及研究者对于证券市场已经有了很长的一段时间的研究。由于发现投机价格与收益率具有关联，因此外国学者对金融市场的价格和收益率进行了大量的研究。为了更好描述经济市场的内部规律，以及经济的波动，来自美国加州大学的Robert Engle研究者在《计量经济学》杂志的一篇文章中第一次提到了ARCH模型。在20世纪80年代有RobertEngle和Grange教授用二元的自回归异方差模型来分析美国通货膨胀率的研究。1986年AndrewA.Weiss思量将自回归异方差模型与双线性时间序列模型进行对照统一。后来，T.Bollerslev提出了GARCH模型。由于金融全球化的感染，国内对于经济波动的研究也越来越多。许多学者也在慢慢运用ARCH模型来对经济市场进行解释。阎海岩经过研究得到，EGARCH和EGARCH-M模型可以较好地模拟沪深两市收益率的变动。徐剑刚和唐国兴运用GARCH-M对深圳和上海的股票市场的变动率采取了研究，得到了模型的预测准确度。上海和深圳市场的股票具有谋利性，并且波动剧烈。王耀通过对比GARCH和Risk Metrics标准法，得出了GARCH可以更精确地预测上海股市变动。楼迎军使用EGARCH研究了上海股市的指数收益率序列和交易序列，得到了各指数序列具备尖峰厚尾的特点，也存在杠杆效应，报酬率与变动性具备负相干性。

目前，我国的市场经济已经开始成长，股票、国债券、政府券、利率市场还未上升至成熟市场的标准[2]。其中国债市场还远达不到弱有效市场，国债指数收益率的数据因为序列自身的联动惯性和经济的滞后性，收益率序列会表现出某些的相关性结合序列本身的尖峰厚尾和异方差性，和投资者承受风险的有偏性，综合解析检验国债指数收益率有序数列的有偏性、异方差性、平稳性、自相关性、尖峰厚尾等特征，确认ARMA-GARCH等价适合于该收益有序数列的研究，用ARMA模型说明收益率数据，用GARCH模型来模拟偏差。由于正态分布不能描述尖峰厚尾，有偏性的特点，思量不同分布的拟合效果与预测效果，探索我国国债指数收益率的模型，为投资者投资和避险提供参考[3]。

2 实证分析

本文选取国债指数的收盘价，共计1 278个数据值，以此观测值建立序列{p}，进而构建其对数收益率序列{r}，建立条件异方差模型。

2.1 序列描述性分析

对序列{p}的数据进行差分，得到新的序列{r}，代表收益率。收益率{r}的时间序列如图1所示：

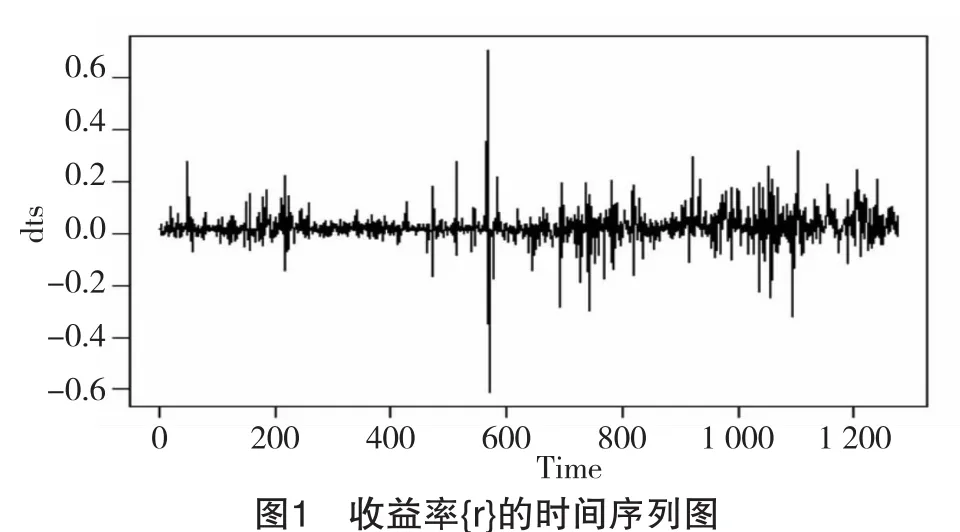
从国债指数收益率序列{r}的线性图1中，可得知收益率在均值上下频繁变动，反映了收益率波动“集群”现象：变动在一段时段内较小，在一段时段段内十分大。

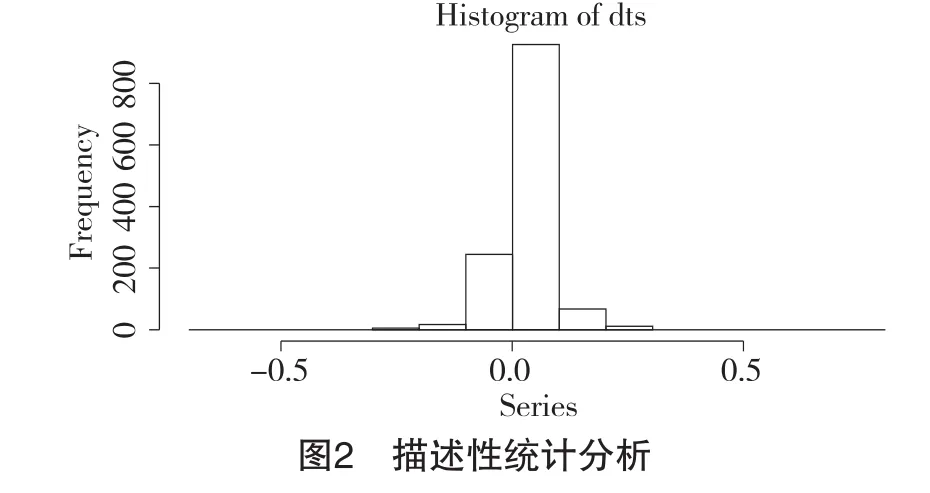
对数收益率的柱形统计由图2可知，国债指数收益率序列呈现出尖峰分布，表明日收益率比正态分布更聚集在均值周围，极度情形出现的几率会高于正态分布下极度情形出现的几率。

2.2 考察序列的平稳性

只有平稳的时间序列，才能直接建立ARMA模型。对时间序列平稳性的验证一般有两种方式：自相关图法和单位根检验法。现今单位根验证有两种多见的方式，ADF验证和PP验证。本文采取ADF检验。由于对应P值＜0.05，不接受序列具有单位根的假设，表明国债指数的对数收益率序列{r}平稳（见图3）。

2.3 序列自相关和偏自相关检验

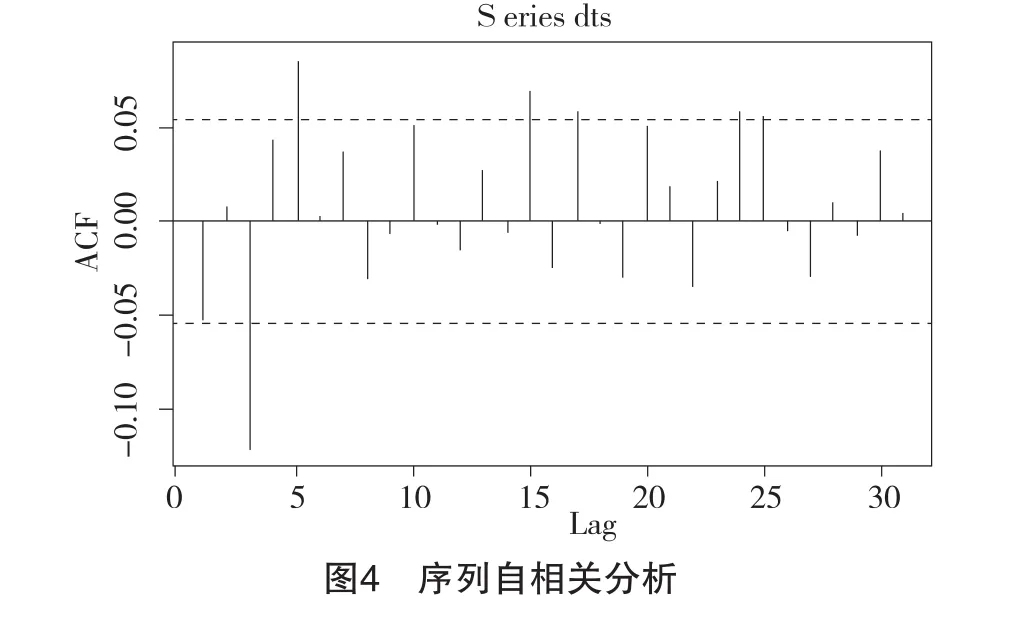
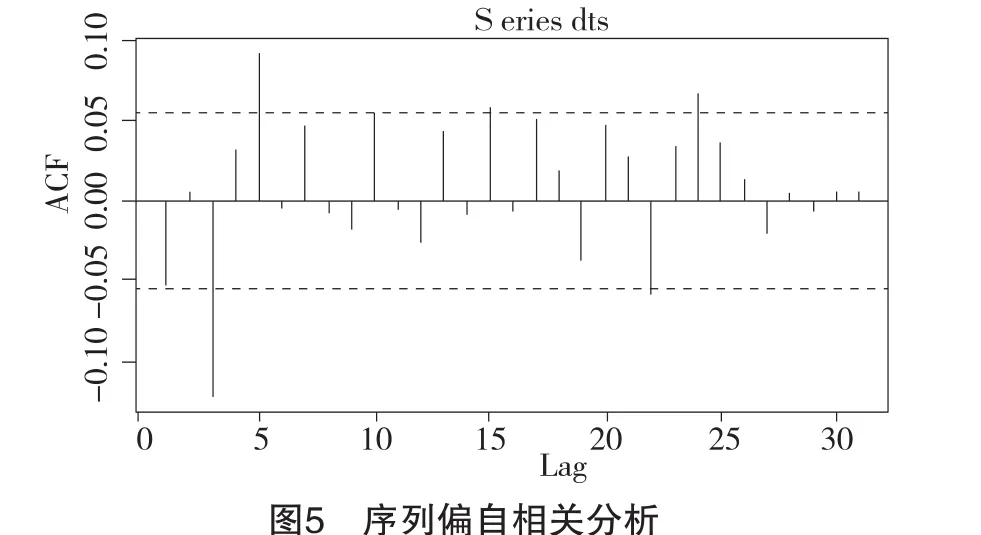
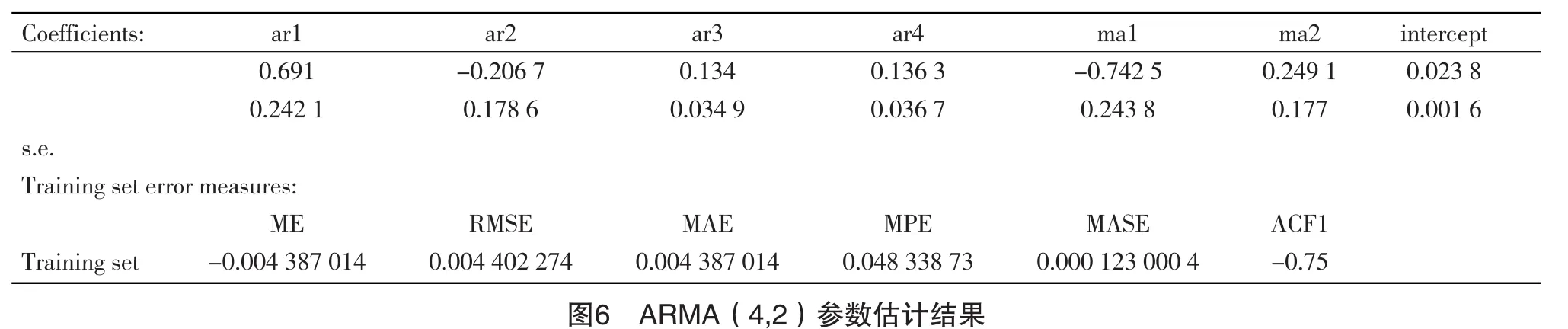
由于收益率在均值上下波动，并没有明显的规律，因此对收益率序列进行自相关和偏自相关检验来判断对数收益率是否随机波动。根据自相关和偏自相关的分析（见图 4、图 5），选取 ARMA（4,2）作为模型。参数估计如图6所示。

2.4 残差检验

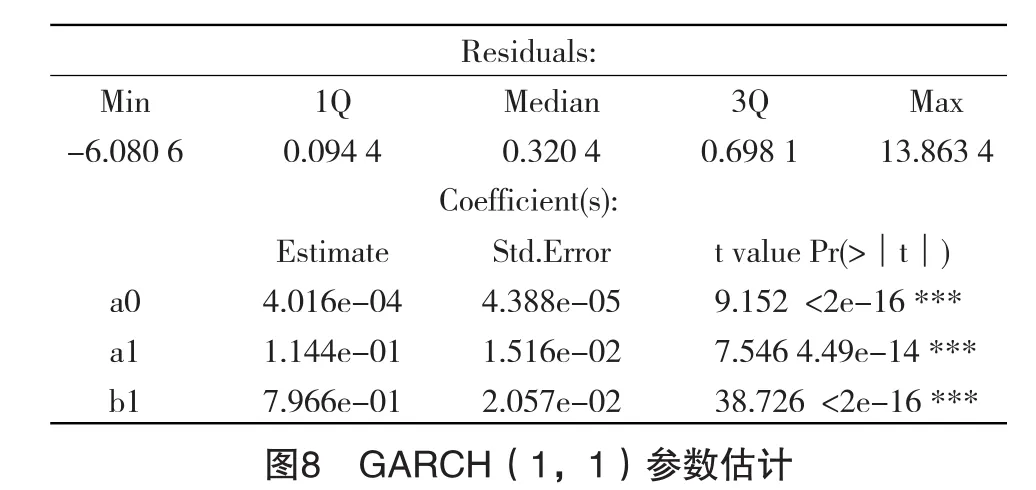
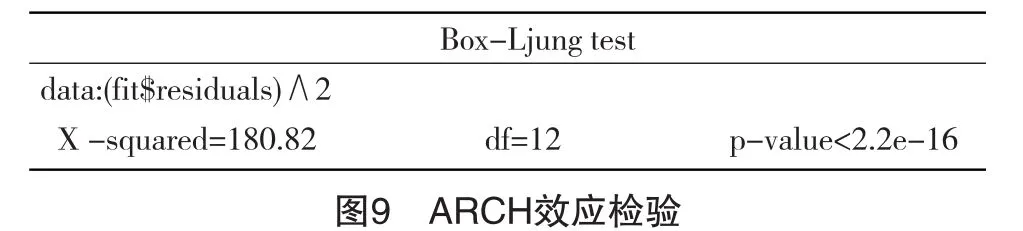
由于p值＜0.05，拒绝不存在ARCH效应的原假设。残差具有ARCH效应，所以建立GARCH模型来拟合残差。选取GARCH（1,1）来刻画条件异方差最简明的情况，故选取ARMA（4,2）—GARCH（1，1）模型进行描述（见图 8）。

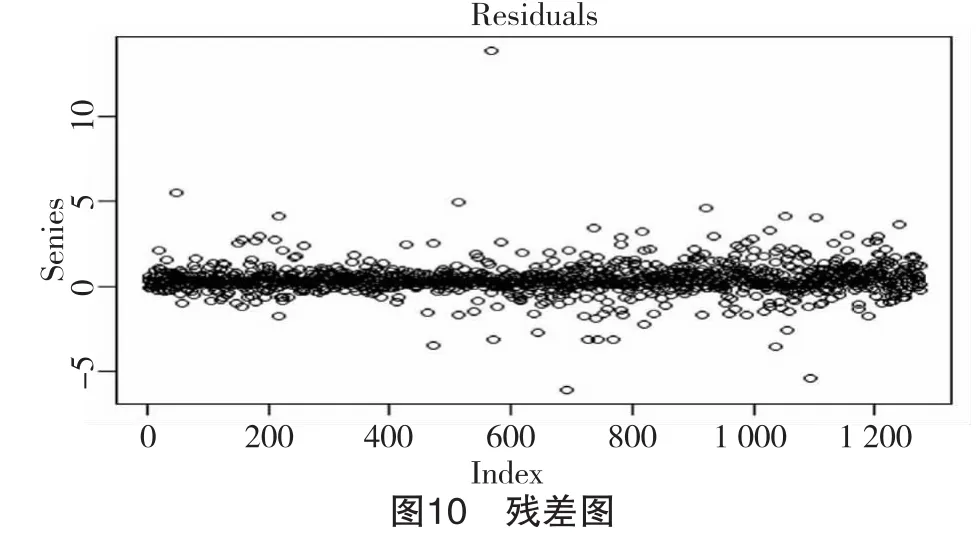
由图 9 发现 ARMA（4,2）-GARCH（1,1）已经消除了ARCH效应，根据图5和图7的拟合结果，可写出方程式（1）、（2）和（3）所示：

rt=0.023 8+0.691 0rt-1-0.206 7rt-2-0.134 0rt-3在建立模型之后，发现残差稳定，波动较小，说明序列得到了较好的拟合。

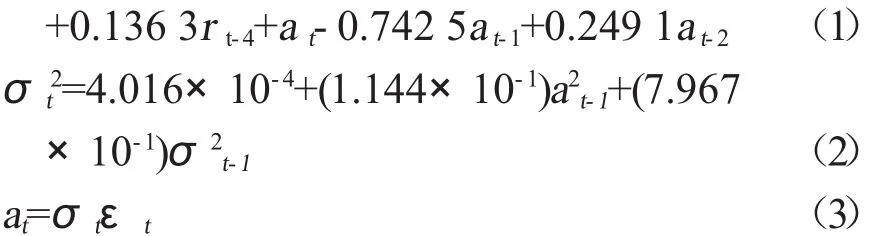
3 结论及建议

本文系统的研究了债券中的国债指数，以国债指数为研究对象，建立了收益率的ARMA-GARCH模型，并有了以下的结论：

①上证国债指数对数收益率存在波动的集聚性，小的变动幅度跟随小的幅度的变动，大幅度的变动后边跟随大幅度的变动；国债指数收益率序列所变现出的长期记忆性是国债指数收益率序列本身所不含有的特性。然而国债指数变动具备长期记忆性预示着某些突然发生的事情会对国债市场产生深远而长久的作用，当前的风险会对未来的决策产生一定期限的影响，这也就意味着波动性在一定程度上是可以被预测的，能够帮助投资者在决策时避免亏损，控制风险服务。

②上证国债指数对数收益率序列变动会有显然的负效应，负面讯息会比相同大小的正面讯息引起的变动还要更大，股票市场也具有相似的特点。通过分析可知国债虽然由国家发行，但债券市场还不能达到弱有效市场，尤其是在近些年来，流动性越来越好，风险和波动性并存。

我国国债市场还在发展的初期，不管是制度的完善还是投资者的能力远不及欧美市场那么成熟，市场情况变化很不确定，波动会随时产生。又因为对波动的研究也是一个很大的工程，本文只是研究了收益率，并没有考虑其他因素，所以本文还是有待加强。债券市场是针对整个市场的所有债券，而本文只是研究了一定时期的国债指数，是有一定的局限性，并不能说明其他债券的变化程度。随着一些政策的出台和市场慢慢发展得比较成熟，这些情况对债券市场的研究造成一定的影响。债券市场的波动不仅与市场本身的运行规律有关，还与国家政策、市场交易制度、宏观经济、经济周期有紧密的关系，将所有经济变量结合才能更有效地研究市场。由于我国的债券市场还未达到弱有效市场，债券市场的研究应该与中国的实际情况结合，才能更精准的研究所要研究的课题。