子午线收敛角和长度比复变函数表示的实数解
2018-10-09金立新魏桂华许常文
金立新,魏桂华,许常文
(1. 中铁第一勘察设计院集团有限公司,陕西 西安 710043;2. 甘肃铁道综合工程勘察院有限公司,甘肃 兰州 730000)
高斯投影是等角横切椭圆柱投影,其必须满足3个条件[1-3]:高斯投影为正形投影,即等角投影;中央子午线投影后为直线,且为投影的对称轴;中央子午线投影后长度不变。
有些学者研究了用复变函数表示的高斯投影[4-6]正反解,公式比较简洁,但需要复数迭代。文献[7]给出了基于复数等角纬度、复数底点纬度表示的高斯投影复变函数非迭代解,但复变函数只能用专用软件计算,故推广使用受到一定影响。文献[8—9]研究了复变函数表示的球面高斯投影公式,并给出了与横墨卡托公式的等价性证明。文献[10]研究了复变函数表示的高斯投影近似式,其特征是采用了椭球面在球面的局部描写,且计算精度较低,只能达到0.3 m。文献[11]在文献[7]的基础上,给出了高斯投影正反解复变函数表示的实数解,也给出了高斯投影正解子午线收敛角和长度比的实数解,但未给出反解子午线收敛角和长度比的实数解。
本文在文献[12]的基础上,进一步研究长度比和子午线收敛角的实数解公式。子午线弧长对等量纬度q的导数和子午线弧长对等角纬度φ的导数分别为
(1)
对式(1)进行解析开拓,即有复数平面坐标对复数等量纬度的导数函数[4-7],复数平面坐标对复数等角纬度Φ的导数函数[4-7],也都是解析函数,公式为
(2)
式(2)即解析函数的复数归化纬度表示。式中,z=x+iy为复数平面坐标;w=q+il为复数等量纬度。将U定义为复数归化纬度,cosU为复数归化纬度的余弦函数。
用复变函数的观点看,长度比和子午线收敛角是解析函数在某点处的导数[4-7]。顾及r=acosu,则式(2)变化为
(3)
式(3)即解析函数导数的复数归化纬度表示。式中,m、γ分别为长度比、子午线收敛角,即
子午线收敛角取负号,是由于复变函数的方向定义与高斯投影定义的方向相反。由此可见,欲求得长度比和子午线收敛角,关键是求得归化纬度和复数归化纬度的表达式。
1 正解归化纬度公式推导
椭球面到平面的正形投影基本方程[12-14]为
z=x+iy=f(q+il)=f(w)
(4)
由复数等角纬度计算的高斯坐标公式[7]为
(5)
根据文献[11],复数等角纬度的虚实部分开形式为
(6)
虚实部分开,即有高斯平面坐标[11]为
(7)
式中系数参见式(41)。N为系数项的项数,式(41)中N=5,实际上可以达到N=8。
由式(6)中的ϑx、ϑy对等量经度、等量纬度l、q分别求导数,可得
由式(7)对复数等角纬度的虚实部分别求导数
由式(7)对等量经度、等量纬度l、q分别求导数
不难验证
表明高斯平面坐标表达为等量大地坐标的函数,是解析函数,满足柯西黎曼条件,是正形投影。即满足了高斯投影正解的第一个条件。
中央子午线成为纵坐标轴,纵坐标即为子午线弧长。顾及tanφ=sinhq,则有
即满足了高斯投影正解的第二个条件。
此时有平行圈半径(等量纬度表示)为
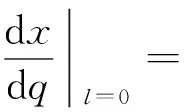
(8)
由式(8),顾及r=acosu,得归化纬度(等量纬度表示)为
(9)
由式(10)得归化纬度(等角纬度表示)为
(10)
由式(10),等角纬度表示的归化纬度,变化为
(11)
利用余弦函数积化和差公式
式(10)变化为
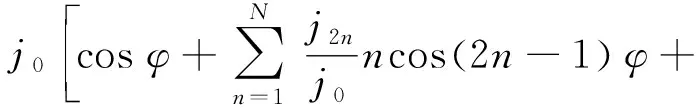
进一步归纳为
(12)
式中,m1=(j0+j2);m3=(j2+2j4);m5=(2j4+3j6);m7=(3j6+4j8);m9=(4j8+5j10)。
2 正解子午线收敛角和长度比
正解中,欲求得子午线收敛角和长度比,关键是将等量纬度、等角纬度表示的归化纬度解析开拓为复数归化纬度。
式(12)解析开拓为复数归化纬度余弦,并顾及式(6),有
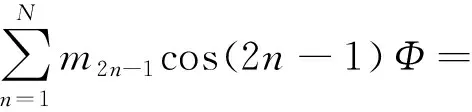
(13)
利用复数三角函数公式
cos[(2n-1)(ϑx+iϑy)]=cos(2n-1)ϑxcosh(2n-1)ϑy-
isin(2n-1)ϑxsinh(2n-1)ϑy
并令
(14)
式(13)虚实部分开,即有
cosU=M-iN
(15)
式(15)代入式(3),即有
(16)
则长度比、子午线收敛角分别为
(17)
(18)
式(17)、式(18)即为由等量坐标q、l表示的长度比和子午线收敛角。
对于中央子午线,有
(19)
式(19)表明在中央子午线上,尺度比为1,即满足了高斯投影正解的第三个条件。
对于赤道,有
长度比随着经度增加而增大,随着纬度增加而减小。子午线收敛角随着经度增加而增大,随着纬度增加而增大。中央子午线上长度比为1,为最小值,离开中央子午线,均大于1。中央子午线及赤道上,子午线收敛角均为0。
3 反解归化纬度公式推导
平面到椭球面的正形投影基本方程为
W=q+il=F(x+iy)=F(Z)
(20)
由等角纬度计算的等距离纬度计算式为
(21)
由等距离纬度计算的等角纬度计算式为
(22)
由复数等距离纬度计算的复数等角纬度计算式为
(23)
或
(24)
利用公式
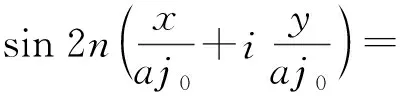
(25)
式(24)虚实部分开,即有
(26)
式中系数参见式(42)。N为系数项的项数,式(42)中N=5,实际上可以达到N=8。
则有等量纬度、等量经度为
(27)
然后,由等角纬度与等量纬度的关系,计算等角纬度
(28)
由式(12)归化纬度与等角纬度的关系,计算归化纬度
(29)
式(29)进一步归纳为
(30)
从式中可以看出,归化纬度依赖于高斯平面坐标的纵坐标与横坐标。式(30)可以直接求取归化纬度,进而求得大地纬度。方法是利用大地纬度与归化纬度的闭合公式,如下
(31)
由式(27),等量纬度、等量经度分别对复数等角纬度虚、实部求导,得
由式(26),等角纬度虚实部分别对高斯平面坐标求导,得
由式(27),等量纬度、等量经度分别对高斯平面坐标求导,得
不难验证
即式(27)满足柯西黎曼条件,即满足了高斯投影反解的第一个条件。
纵坐标轴成为中央子午线,顾及tanφ=sinhq,则有
横坐标轴成为赤道,有
即满足了高斯投影反解的第二个条件。
4 反解子午线收敛角和长度比
反解中,欲求得子午线收敛角和长度比,关键是将等距离纬度、高斯投影平面坐标表示的归化纬度解析开拓为复数归化纬度。
式(30)解析开拓为复数归化纬度余弦,并顾及式(6),有
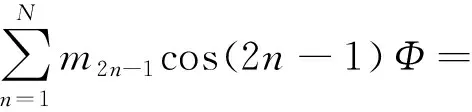
(32)
根据文献[11],复数等角纬度的虚实部分开形式为
(33)
利用复数三角函数公式
cos[(2n-1)(φx+iφy)]=cos(2n-1)φxcosh(2n-1)φy-
isin(2n-1)φxsinh(2n-1)φy
式(32)虚实部分开,即有
cosU=P-iQ
(34)
并令
(35)
式(34)代入式(3),即有
(36)
长度比、子午线收敛角分别为
(37)
(38)
对于中央子午线,有
(39)
式(39)表明在中央子午线上,尺度比为1,即满足了高斯投影反解的第三个条件。
对于赤道,有
长度比随着横坐标增加而增大,随着纵坐标增加而减小。子午线收敛角随着横坐标增加而增大,随着纵坐标增加而增大。中央子午线上长度比为1,为最小值,离开中央子午线,均大于1。中央子午线及赤道上,子午线收敛角均为0。
5 步骤及算例
5.1 高斯投影正解的计算步骤
首先,由大地纬度B计算等量纬度
q=arctanh(sinB)-e·arctanh(esinB)
(40)
其次,根据式(6),由等量大地坐标q、l求出复数等角纬度Φ的虚实部分开形式ϑx、ϑy。
然后,由式(10)计算归化纬度余弦。由式(14)计算复数归化纬度余弦的虚实部,即过渡变量M、N。
正解系数为
(41)
最后,由式(17)、式(18)计算长度比、子午线收敛角。
5.2 高斯投影反解的计算步骤
首先,计算底点纬度半径R=aj0。
其次,由式(25)计算复数等角纬度的虚实部分开形式φx、φy。由式(29)、式(30)计算归化纬度余弦、等量经度cosu、l。
反解系数为
(42)
然后,由式(31)计算大地纬度,由式(36)计算过渡变量P、Q。
最后,由式(38)、式(40)计算长度比、子午线收敛角。
5.3 算 例
采用CGCS2000椭球元素,利用本文推导的公式,编制mathematica计算机代数系统程序,按照先正解、后反解的顺序,计算几个点的长度比和子午线收敛角,结果见表1。
从表1可以看出:反解的长度比和子午线收敛角与正解的长度比和子午线收敛角,完全一致。
6 结 论
(1) 本文定义了复数平行圈半径、复数归化纬度,补充了高斯投影复数理论,丰富了高斯投影理论。
(2) 给出了正反解长度比、子午线收敛角的新公式,对于研究高斯投影的机理、性质有一定意义。
(3) 基于复数纬度的实数解,突破经典高斯投影带宽的限制,适应半带宽可非常接近90°,可以实现图形信息的连续表达,对于高斯投影理论有一定改善。

表1 计算结果
