大坝变形时间序列的奇异谱分析
2018-10-09李世友王奉伟沈云中
李世友,王奉伟,沈云中
(同济大学测绘与地理信息学院,上海 200092)
大坝变形受时效、温度和水位等确定性因素[1-2]和许多非确定性因素的影响,其变形序列中既有低频信号也有高频信号,因此对大坝变形的分析和预测通常十分困难。目前,大坝变形预测的方法主要有灰色模型[3-4]、时间序列分析(ARMA)[5-6]、多元线性回归[7]和神经网络模型[8-9],这些方法纯粹从数学或机器学习的角度出发分析变形时间序列。王新洲等[10]用WT-SVM把变形时间序列分解成具有不同频率特征的分量,分别预测各分量并进行重构,但没有分析大坝变形的各变形因子。奇异谱分析法(singular spectrum analysis,SSA)是一种与经验正交函数相联系的统计技术,具备从含有强背景噪声的时间序列中有效提取信号的能力,特别适合研究周期振荡行为的分析方法。本文拟利用SSA分析大坝变形监测时间序列,提取趋势项和周期项,分析其变形影响因子,并建模预测大坝的变形趋势。
1 奇异谱分析法
奇异谱分析法由Broomhead等[11]提出并用于处理气象数据,该方法不需要事先假定信号类型,利用经验正交函数将时间序列数据分解成以信号为主的子空间和以噪声为主的子空间,利用信号为主的子空间数据分析序列的时间演变特征。
SSA[12-14]根据一维时间序列X=(x1,x2,…,xN),构建轨迹矩阵D如下
(1)
式中,M为窗口长度。对于非平稳序列,根据轨迹矩阵计算协方差阵C如下
C=DDT
(2)
对协方差阵C进行特征值分解,确定特征值λk及对应的特征向量Vk(由大到小排列)。第k个特征值对应的主成分为
(3)
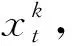
(4)
利用所有M个主成分可完全恢复原始序列X=(x1,x2,…,xN)。如果前r个主成分的贡献统计上属于信号子空间,则利用这些主成分重构时间序列的信号部分如下
(5)
其余部分属于噪声子空间,可用于重构时间序列的噪声。
2 大坝变形的奇异谱分析
试验采用我国某大坝2004年5月1日至2010年8月31日单点的径向形变GPS监测数据(向河流上游为负,下游为正),同时采集了大坝的水位数据和坝区的温度数据,采样间隔为1 d,数据长度N为2314。因为采集的数据序列存在一定的缺失或粗差,试验前要对数据进行预处理。首先对各项数据进行粗差探测并剔除。对于数据缺失插补问题有很多解决方法,如Shen等[15]在Schoellhamer[16]研究的基础上提出了一种改进的奇异谱分析插补方案(ISSA)。本文对于缺失的数据序列采用三次样条插值方法进行插补。
窗口长度M对于提取和分析信号具有很大的影响,选取时通常会考虑周期分量的识别效果,一般取周期的整数倍且满足N/3≤M≤N/2[17]。通过试验对比,选取窗口长度M为730(约2年),以便能较好地提取出各时间序列中的信号成分。用SSA分析大坝变形时间序列(如图1所示),前50个特征值曲线如图2所示,提取的信号分量如图3所示。由图2和图3分析可知,第一个分量是趋势项,能量贡献占信号总能量的92.98%;第二和第三个分量为一对周期分量,周期为1.00年,能量贡献率和为6.29%;第四和第五个分量也是一对周期分量,周期为0.78年,能量贡献率和为0.11%。趋势和周期分量的能量和占信号总能量的99.38%,余量占比0.62%即可归为噪声部分。为了进一步分析各变形分量与温度和水位因子的关系,利用SSA分别提取温度和水位数据中的周期分量,具体如图4、图5所示。
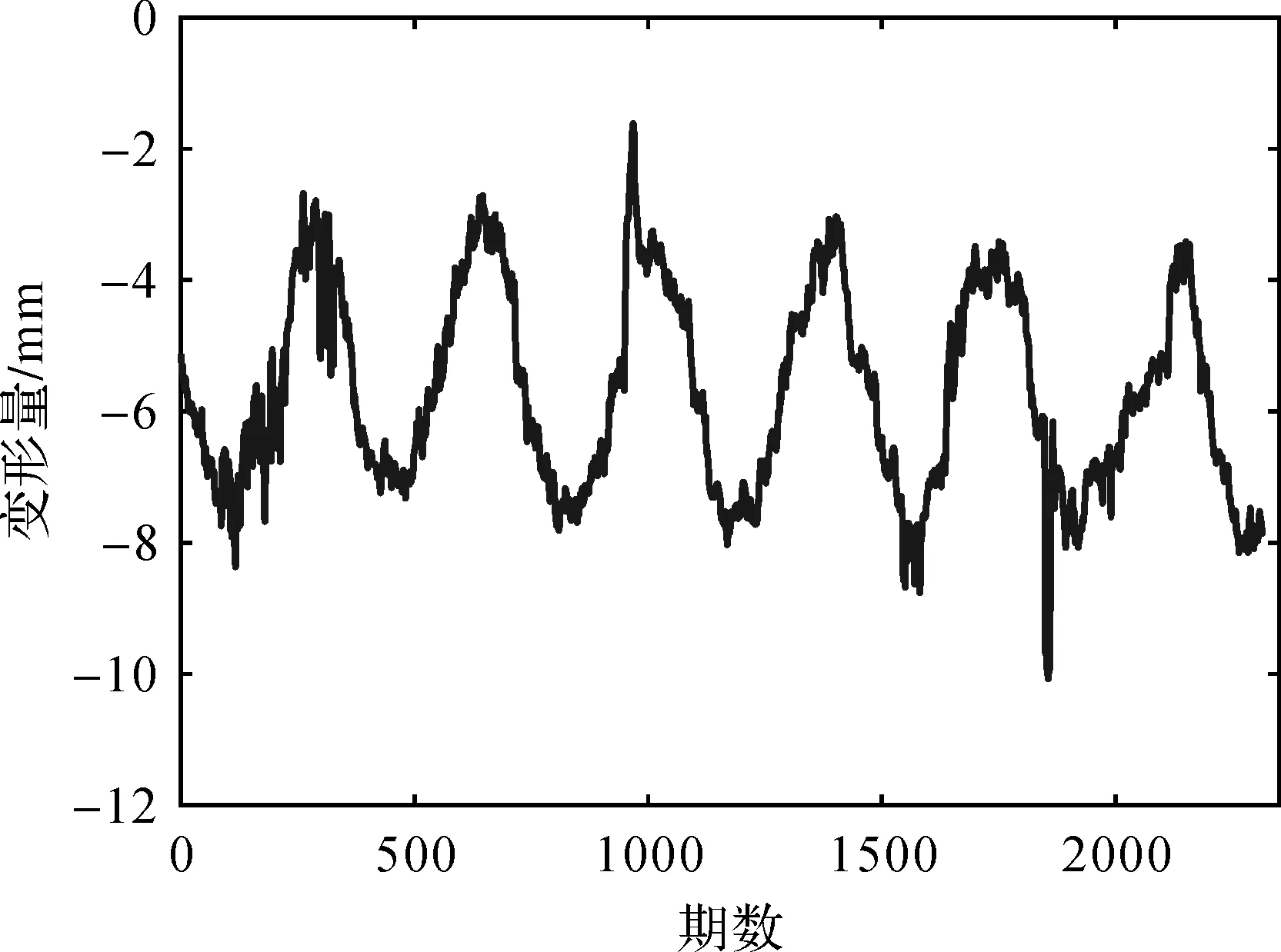
图1 大坝变形时间序列
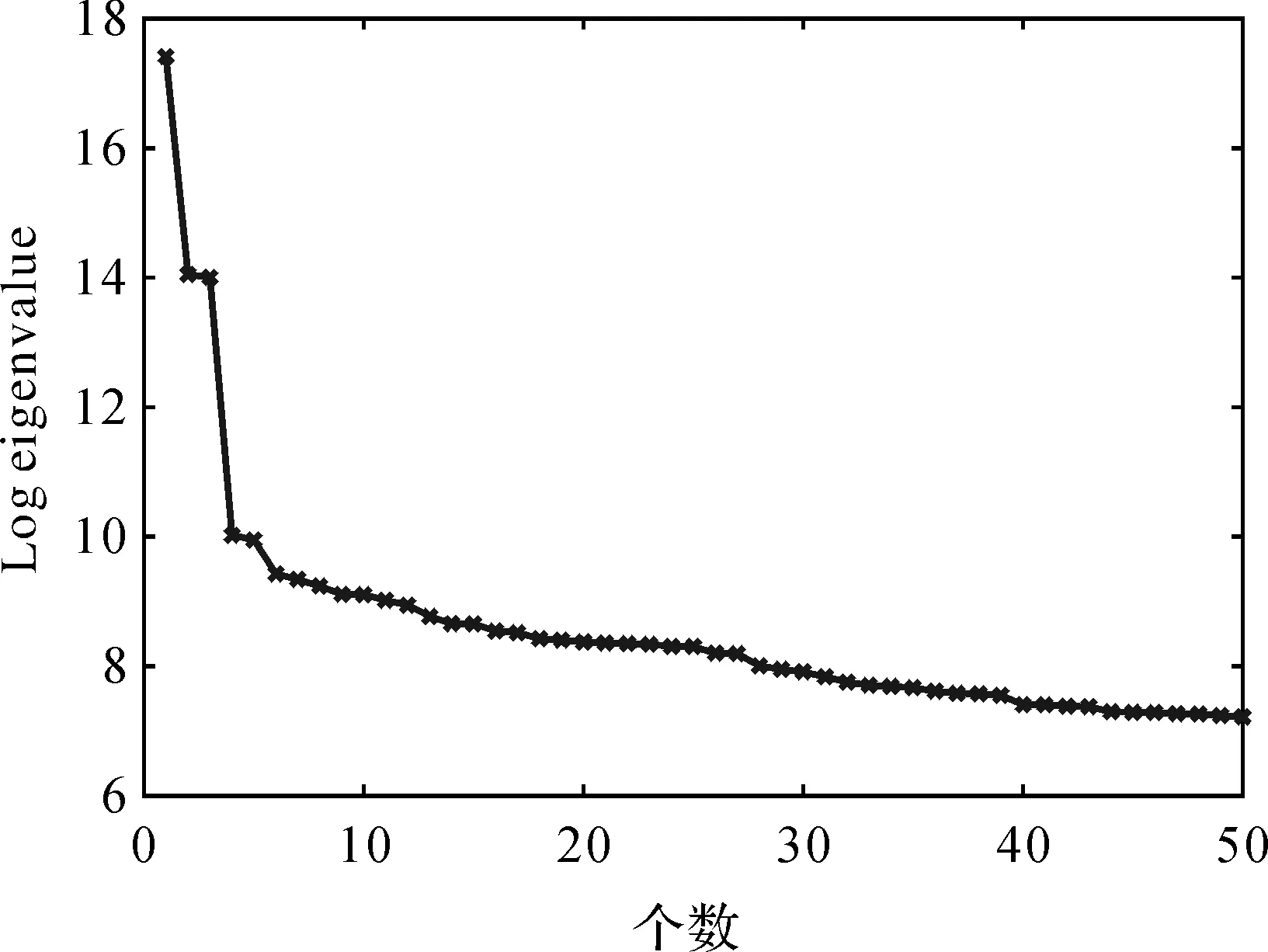
图2 特征值曲线(前50个)
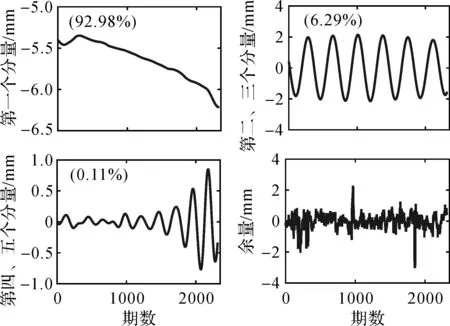
图3 SSA提取趋势和周期分量及其贡献率
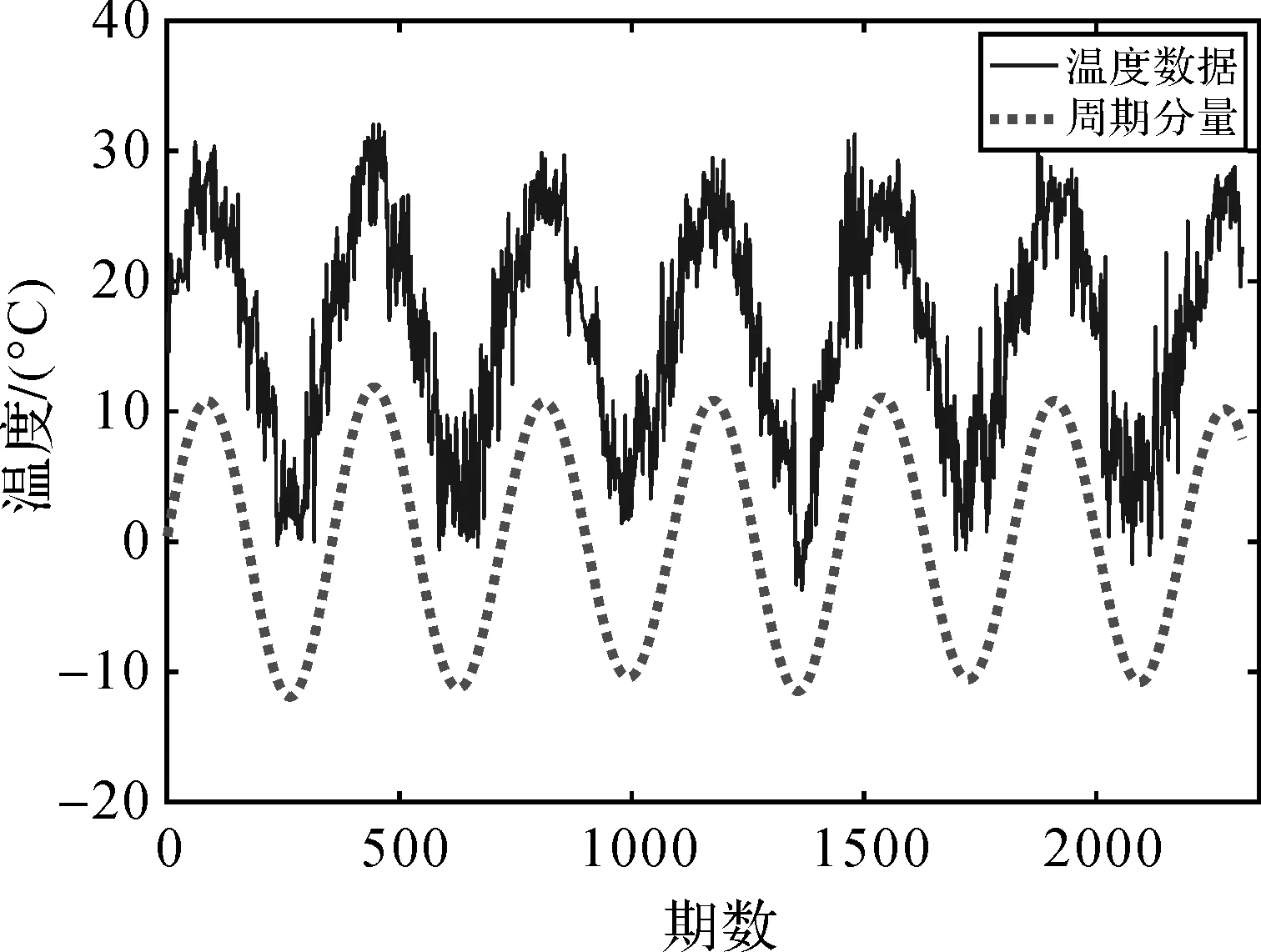
图4 温度数据及其周期分量
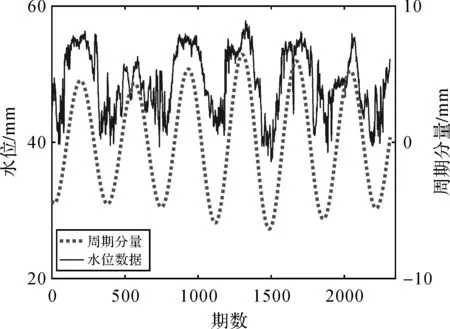
图5 水位数据及其周期分量
从SSA分析结果可以发现:大坝由于长期的外力荷载存在徐变,表现为趋势分量,主要与时效有关。从大坝变形时间序列中提取出了周期为1.00年的一个分量,同时从温度和水位数据中也提取出了周期分别为1.00年和0.99年的分量。由此可知,大坝存在约1年的周期弹性形变,且主要与温度和水位的周期变化相关。比较大坝变形、温度和水位的周期分量(如图6所示)可以发现:大坝周期弹性形变与温度呈明显的负相关,且变化趋势几乎同步;大坝形变与水位变化呈正相关且存在一定的相位差。
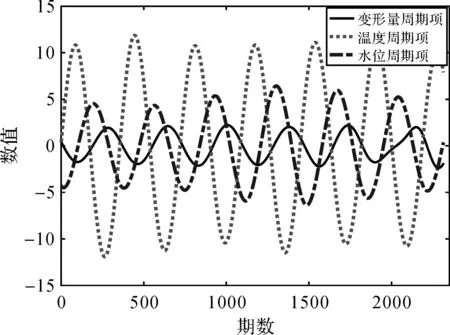
图6 SSA提取形变、温度、水位的周期分量
大坝在自重和水压等荷载作用下可能发生徐变,导致大坝明显地向上游或下游趋势性变形。温度和水位因子对大坝变形的影响主要为:温度升高,大坝向上游的变形位移增大,相反温度降低,则向下游的位移增大;水位升高,其向下游的变形位移增大,反之则向上游的位移增大[18]。为进一步分析趋势项和周期项与影响因子的相互关系,求解大坝变形趋势分量、周期分量(两个周期分量之和)和余量与影响因子(时效、温度、水位)的相关系数(见表1)。大坝变形的趋势分量主要与时效因子有关,相关系数为-0.957 0,表明徐变方向为整体向河流上游(向河流上游为负,下游为正)。大坝变形的周期成分与温度因子的相关系数为-0.870 4,与考虑相位差的水位因子相关系数为0.489 4。结合图6可以看出,温度升高大坝向上游变形,降低则向下游变形;水位升高大坝向下游变形。降低则向上游变形。这与温度和水位因子影响大坝变形的规律基本一致。
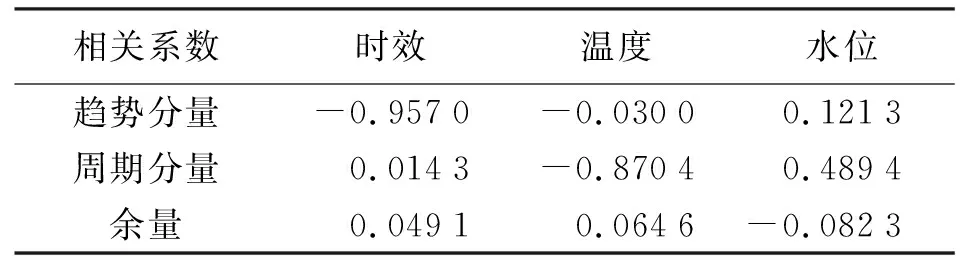
表1 大坝变形与各影响因素相关系数
3 大坝变形预测
受地质、气候、施工方案等各种条件的影响,大坝在施工或运营过程中总会发生不同程度的变形,及时掌握并准确预测大坝变形状态,对大坝安全具有重要意义。目前常用的预测方法主要有时间序列模型、灰色理论等,但由于大坝变形具有较强的非平稳性和非线性,这些方法的应用均受到了一定限制。SSA能有效地将时间序列中的信号和噪声分离,根据图3可知,前5个分量为趋势和周期分量,其能量之和占总能量的99.38%,余量可归为噪声部分,因此信号的重构阶数r=5。
为了避免计算时各因子的数量级相差过大而导致矩阵病态,建模前将时效因子数据归化为年序列。取样本数据中前2200个作拟合建模,后114个用于检核。文中分别对SSA提取的不同分量建模再叠加作为大坝变形的预测结果,流程如图7所示。
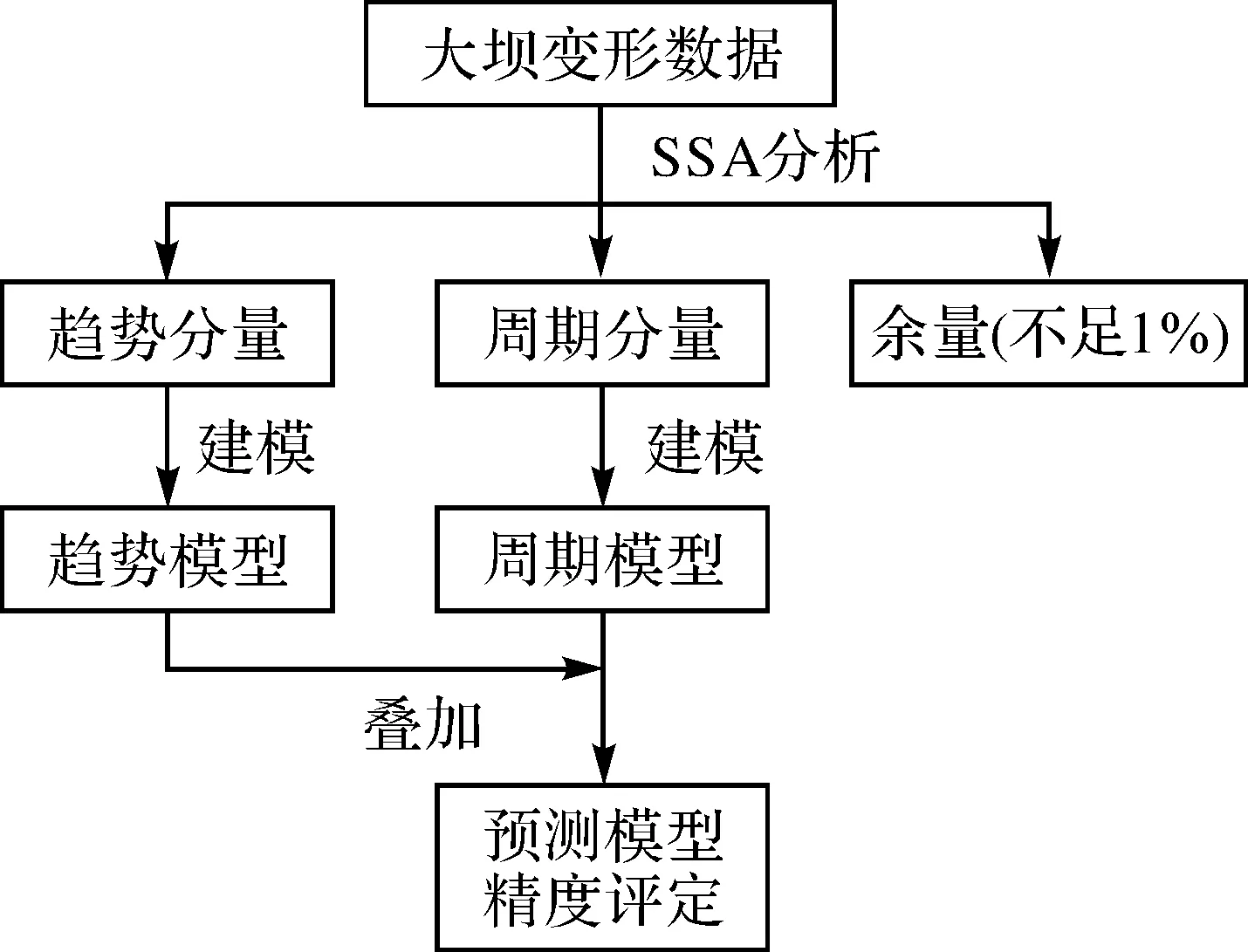
图7 大坝变形预测流程
采用式(6)拟合变形信号中的趋势分量
f(t)=P0+P1t+P2t2+P3t3+P4t4
(6)
采用式(7)拟合提取的第二和第三个分量,即第一个周期分量
g(t)=a0+a1cos(ω1t)+a2sin(ω1t)
(7)
采用式(8)拟合提取的第四和第五个分量,即第二个周期分量
h(t)=b0+b1cos(ω2t)+b2sin(ω2t)+b3cos(2ω2t)+b4sin(2ω2t)+b5cos(3ω2t)+b6sin(3ω2t)
(8)
最后根据最小二乘原则解得式(6)—式(8)的各项系数(见表2)。
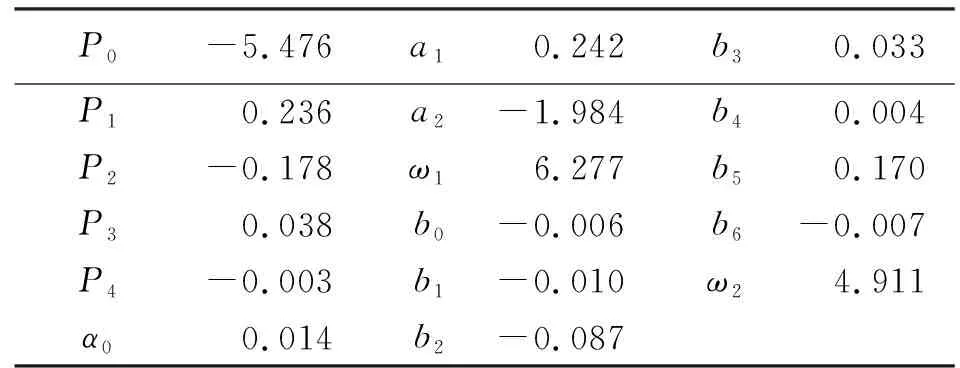
表2 模型系数
为了验证上述方法的效果,将文中模型与传统的多元线性回归(multiple linear regression,MLR)模型作比较,根据确定性因子时效、温度、水位建立多元线性回归模型如下
y=β0+β1t+β2T+β3h+ε
(9)
式中,t、T、h分别代表时效(年)、温度(℃)和水位(mm)。求得各项系数β0、β1、β2、β3分别为0.802、-0.133、-0.163、-0.070。
从图8和图9可知,SSA预测与多元线性回归预测结果相比,其更逼近真实值,预测残差明显小于多元线性回归模型,预测精度较高。为了定量评价模型的预测性能,利用均方根误差(RMS)和平均绝对误差(MAE)两个指标对模型的预测效果进行评估
(10)
(11)
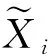
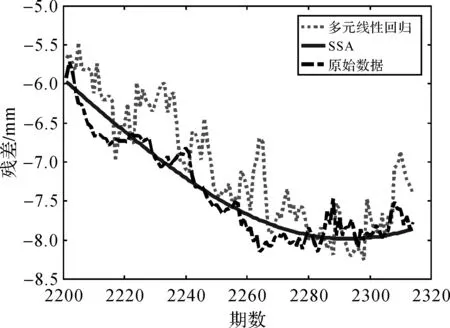
图8 两种模型预测结果与真实数据对比
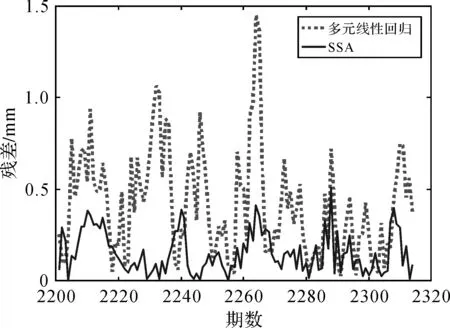
图9 两种模型预测结果残差对比
SSA方法拟合和预测的RMS值为0.52、0.24 mm,明显小于多元线形回归模型的0.81和0.57 mm,具体精度指标见表3和表4。结果表明,SSA方法的拟合及预测精度明显优于多元线性回归,能更准确地预测大坝变形。
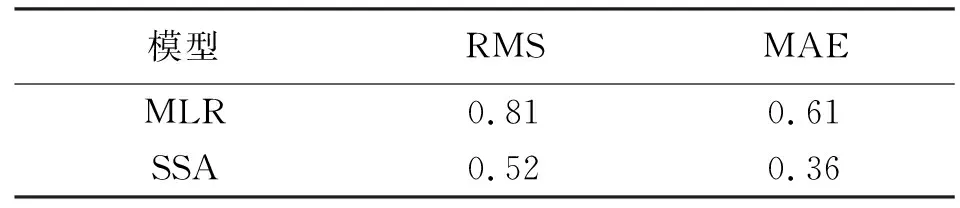
表3 两种模型的拟合精度评价指标 mm
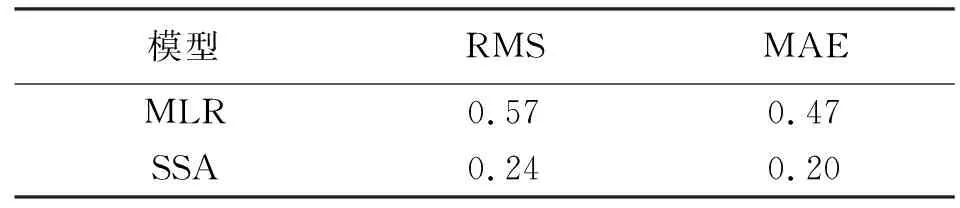
表4 两种模型的预测精度评价指标 mm
4 结 语
本文利用SSA方法对大坝变形时间序列进行分析,提取了趋势项和周期项。通过分析发现,大坝存在徐变和周期性弹性形变,对周期性弹性形变的分析发现,温度因素对其影响作用明显大于水位。最后利用提取的趋势和周期分量对大坝变形时间序列进行拟合并预测,并与传统的多元线性回归进行对比。通过实例分析,SSA与多元线性回归模型的拟合和预测的均方根误差分别为0.52、0.24 mm和0.81、0.57 mm;平均绝对误差分别为0.36、0.20 mm和0.61、0.47 mm。SSA方法的拟合和预测误差均小于多元线性回归,表明本文方法能更为准确地预测大坝的变形。但本文仅采用了单一变形点数据,不能从整体上反映大坝变形的内部规律,分析多点的大坝整体变形是下一步研究的重点。
