利用蒙特卡罗计算重积分的改进算法
2018-10-09王丙参魏艳华贾金平
王丙参,魏艳华,贾金平
(天水师范学院 数学与统计学院,甘肃 天水 741001)
0 引言
蒙特卡罗方法(M-C,即随机模拟)是利用计算机生成随机数并通过模拟随机现象来进行近似计算的方法。在工程、科学等领域中,实验数据很难获得或成本太高,这时蒙特卡罗方法就是最经济、实用的方法[1-4]。另外,对于一些复杂问题,比如方程组求解、最优化、偏微分方程的解等,蒙特卡罗方法也非常有效,但它最常用的还是计算积分,是利用数值方法计算多重积分的首选方法,且积分维数越高,效率也越高。一般情况下,在蒙特卡罗算法中,利用均匀随机数计算积分简单,但精度不高,误差与被积函数方差和模拟次数有关。通过增加模拟次数提高精度的速度太慢,且耗时过多,尤其对于多重积分问题更加严重。如果改进蒙特卡罗方法,可以缩减积分估计的方差,那就能提高估计的精度和可靠性[5-8]。
本文比较研究了计算重积分的随机数法,并利用重点抽样技术改进重积分的蒙特卡罗计算,提高了抽样效率,得出有利随机数法是重点抽样法的特例,误差较小。
1 利用随机数法计算重积分
很多物理问题都可转化为多重积分的计算问题,在实际计算中,经常发现被积函数的原函数很难求出,或原函数不是初等函数,对于这样问题,最好设计一种蒙特卡罗方法进行近似计算[7,8]。
方法1:均匀随机数法
(1)取包含D(积分区域)的矩形区域Ω:a≤x≤b,c≤y≤d,其面积SΩ=(b-a)(d-c)。(2)生成 Ω 上均匀随机数列 (xi,yi),i=1,2,…,n,不妨设前k个随机数落入积分区域D,则当n充分大时,
方法2:一般随机数法
(1)取包含D(积分区域)的矩形区域Ω:a≤x≤b,c≤y≤d,其面积SΩ=(b-a)(d-c)。
(2)取概率密度函数g(x,y),使得
(3)生成随机数列 (xi,yi)~g(x,y),i=1,2,…,n,不妨设前k个随机数落入积分区域D,则当n充分大时,
方法3:有利随机数法
由于f(x,y)=ln(1+2x+2y)的原函数为所以积分I的精确解为F(1,1)-F(1,0)-F(0,1)+F(0,0)=1.057615826853317。
利用 MATLAB 内置函数 dblquad(′log(1+2*x+2*y)′,0,1,0,1)可得数值积分为1.057615735740697。虽然数值积分的精度已经很高,但随着维数增加,它的计算效率显著降低,而蒙特卡罗方法的精度与积分维数无关。下面利用蒙特卡罗方法计算积分I。
对f(x,y)在进行泰勒展开,可得f(x,y)=ln(1容易估算出I≈ln3,故取有利概率密度函数
程序中取100个随机数,做了1000次模拟,其中,平均误差等于模拟值减去真实值的绝对值的平均值,模拟结果如下:
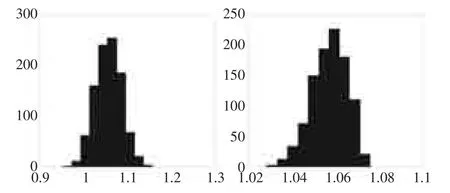
图1蒙特卡罗积分值的直方图(左:均匀随机数法,右:有利随机数法)

表1 1000次模拟的均值、方差和平均误差
由图1和表1可知,不论用均匀随机数序列还是有利随机数列,蒙特卡罗积分值的分布都近似服从正态分布,分别为:

均匀随机数法的方差与平均误差明显大于有利随机数法的方差与平均误差,这说明有利随机数法的模拟结果更靠近真值(1.057615826853317),即有利随机数法的误差更小,更可靠。
2 利用重点抽样技术改进重积分的蒙特卡罗计算
假设包络函数g(x)在分布族{g(x;λ)}中取得,其中参数λ为限制条件,则目的就是在给定限制λ的条件下,求解:
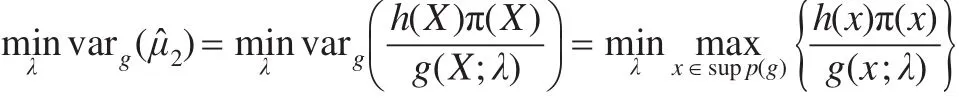
其中,supp(g)表示g的支撑。

即Jenson不等式等号成立的充要条件。可见,当x(i)~g∝|h|π(x)时,有:

由于Eπ[h(X)]为常数,故最优包络函数g*不同于密度函数π。如果π(x)≫g(x),其中x为来自g(x)的抽样,则权重会变得很大,从而估计方差也会变得很大,因此选取合适的包络函数g(x)才能降低估计的方差。要使得估计方差足够小,试验分布g(x)的形状要尽可能接π(x)h(x),特别地,g应有一个比π(x)更长的尾部,并可以很方便从g(x)中抽取样本。尽管有时候无法或很难在高维空间找到一个恰当的试验分布,但这却是重点抽样的主要任务。
当直接从目标分布π(x)抽样很难,而从包络函数g(x)中抽样和计算权重w(x)容易时,重点抽样法有效,但是有效的高低很难估计,一个不太精确但有用的方法是:利用有效样本的大小进行衡量。可解释为:从试验分布中抽取n个权重样本相当于从目标函数中近似抽取EES(n)个独立同分布的样本。
在高维重点抽样中寻找一个好的试验分布是很困难的。一个解决办法就是循序地构造试验分布函数。假定x=(x1,…,xp),其中每个xi仍可为多维随机向量,则试验分布可构造如下:

其中x≤p=(x1,x2,…,xp)。同样,根据x的分块,给出目标分布的分解:
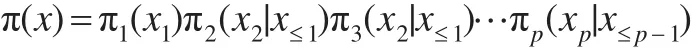
这样,未标准化权重可写为:

该式建议从g1(x1),g2(x2|x≤1),…,gp(xp|x≤p-1)中序贯抽取X的各分量。令,则有递推关系:
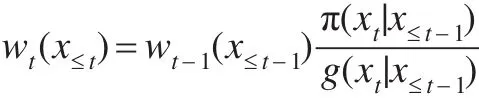
显然,wp(x≤p)=w(x)。这个方法具有如下优点:
(1)如果序贯产生的部分样本计算得到的权重值太小,则可停止进一步产生x的分量。
(2)可利用 π(xt|x≤t-1)来设计g(xt|x≤t-1),即有目标分布π(x)的边际分布指导x的产生。
这个方法听起来很令人兴奋,但是不切实际的,因为条件分布π(xt|x≤t-1)往往是得不到的,甚至得到条件分布比原问题还困难。为了实现序贯抽样,引入更复杂的一些步骤。假定可找到一系列辅助分布π͂(x≤t-1)来近似边际分布π(x≤t-1)。需要强调的是,仅需知道除了归一化常数外的 π͂(x≤t-1),并且在构造整个样本x=(x1,…,xp)时仅起到指导作用,而不一定需要从中抽样。这样,可用如下的递推过程来进行序贯重点抽样(SIS):
(1)从g(xt|x≤t-1)中出去样本xt,并令x≤t=(x≤t-1,xt)。
在序贯重点抽样中,ut称为增量权。使用序贯重点抽样的原因是:利用辅助分布π͂(x≤t-1)可构造更有效的试验分布,并将一个极其困难的任务分解为多个易处理的小任务,从而增加了可行性。
重点抽样利用不是来自π(x)中的随机样本X(1),…,X(n)估计目标μ=Eπ(h(X)),假如存在一个正确的权重集与随机样本相关,同时这些权重不是太不对称,则样本几乎可从任何分布中抽样。如果对于任意二次可积函数h(x)成立:
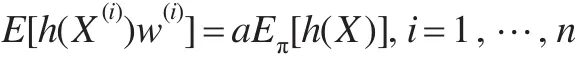
其中,a为全部n个样本的共同归一化常数,则称加权随机样本集关于 π 是正确的。
容易证明,如果wt-1(x≤t-1)是x≤t-1关于 π≤t-1的正确权,则wt(x≤t)是x≤t关于 π≤t的正确权。因此,用最后得到的正确权wp对序贯方式得到的目标分布π(x)的整个样本x赋予了正确权。
加权样本的实质是为了强调对任意给定的样本X存在多种加权w的方法,在重点抽样中,权重w对应样本X的一个确定函数,比如,这种情况下,(w,X)s得加权变量w为非退化随机变量。

(1)原始蒙特卡罗算法:生成n对随机样本(x(1),y(1)),…,(x(n),y(n)),(x(i),y(i))~π ,其中 π 服从[-1,1]×[-1,1]上的均匀分布,因为:
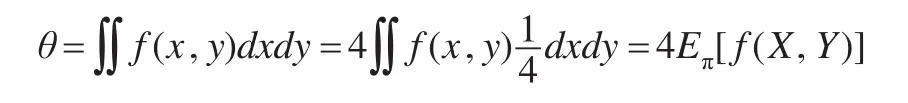
所以该积分的估计为:
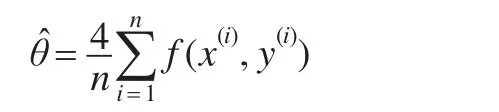
在每次模拟中,令n=5000,共模拟m=100次,模拟结果见图2左。
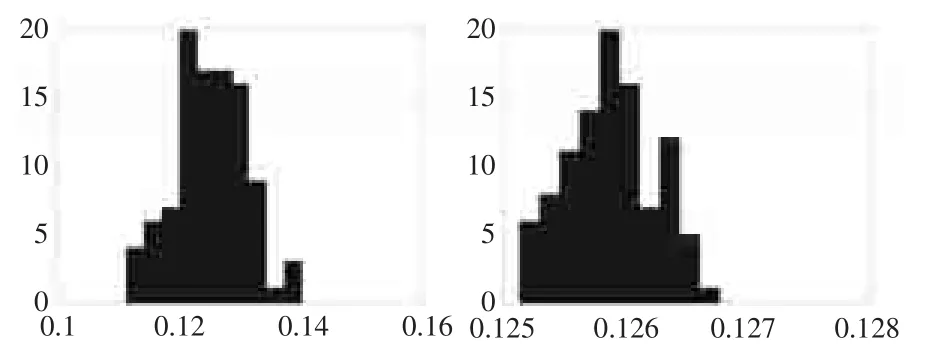
图2原始蒙特卡罗(左)与重点抽样(右)的100次模拟结果直方图

(2)对函数f(x,y)做直观分析后,决定选用试验分布g(x,y)进行重点抽样,其分布形式为:
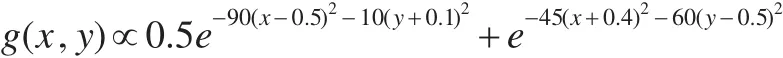
其中 (x,y)∈χ=[-1,1]×[-1,1]。这是一截尾混合高斯分布:利用如下步骤从这一混合高斯分布中抽样:
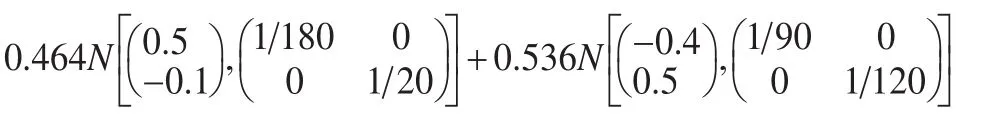
生成均匀随机数u~U(0,1),如果u≤0.464,则生成随机数否则,生成随机数
落入区域χ外时,舍去。
在每次模拟中,令n=5000,共模拟m=100次,模拟结果见图2右。
θ̂=0.1259,std(θ̂)=3.7462e-004
显然,利用重点抽样技术,蒙特卡罗的标准误差减少了很多,大大提高了抽样效率,这是因为始蒙特卡罗存在与确定性方法同样的问题:将大量的时间浪费在计算那些函数值几乎为0的随机样本上。
