GNSS多系统组合测速模型与精度分析

吴超

(中国铁路设计集团有限公司测绘地理信息研究院,天津 300143)

0 引 言

当前的导航卫星系统包括四大全球导航卫星系统,即美国的GPS、俄罗斯的GLONASS、中国的北斗导航卫星系统(BDS)、欧盟的全球导航卫星系统Galileo,此外，还有日本的QZSS、印度的NaviC等区域导航卫星系统,随着各国各地区导航卫星系统的蓬勃发展,多GNSS系统组合导航定位、定轨及其应用成为研究的热点[1-6]。GNSS测速的研究主要是GPS、BDS的单系统原始多普勒测速[7-9]、导出多普勒测速[7-18]以及GPS原始多普勒与导出多普勒组合测速[4,19],也有学者对GPS/GLONASS组合测速进行了探讨[4],但对多GNSS系统组合测速缺少系统的分析与讨论。

本文在多普勒观测值的基础上,给出了GNSS多系统组合测速的数学模型,结合高频GNSS实测数据,分别对多GNSS系统组合条件下原始多普勒测速、导出多普勒值测速及二者组合测速精度进行了分析。

1 数学模型

GNSS多普勒频移是由卫星和接收机之间的相对运动引起的,原始多普勒观测值则是通过锁相环直接估计的相位率观测值。GNSS多普勒观测值可以近似写为[20-21]

(1)

将式(1)多普勒频移观测值转化为距离率,可得GNSS多普勒观测方程:

(2)

其中:ρ为几何距离;dtr为接收机钟差;dtj为卫星钟差;Ii为电离层延迟;T为对流层延迟; ·为各项的变化率。

由式(2)可将误差方程写为

(3)

多系统测速时,除了统一其坐标系统及时间系统外,还需要考虑系统间偏差,在参数估计时为每个系统添加一个钟差变率参数,或者选择某一个卫星系统为参考,添加一个接收机钟差变率偏差参数。本文采用第一种方法,即每个系统添加一个接收机钟差变率参数。由此,多系统组合测速误差方程可写为

(4)

2 算例分析

多普勒测速包括原始多普勒测速和导出多普勒测速,本文分别对这两种测速方法进行测试,测试组合包括GPS、BDS、GLONASS、GPS/BDS、GPS/GLONASS、BDS/GLONASS、GPS/BDS/GLONASS、GPS/BDS/GLONASS/Galileo/QZSS,然后对原始多普勒观测值和导出多普勒观测值组合时对系统测速精度进行了测试,这里的导出多普勒观测值采用相位观测值的一阶中心差分导出。在原始多普勒和导出多普勒观测值组合测速时,由于前人研究的结果是原始多普勒测速在厘米每秒的量级,而导出多普勒测速在毫米每秒的量级,二者权比设为1∶100.

采用天宝R10接收机采集的一段约30 min静态GNSS数据进行测试,采样率为20 Hz,在精度评价时以零值作为真值计算RMS.图1示出了测试数据在该时段内的可见卫星数,图2示出了相应历元时刻的PDOP值,可以看出多系统组合时可见卫星数明显增加,改善了卫星的几何结构,相应的PDOP值明显减小。

2.1 原始多普勒测速

基于原始多普勒观测值的GNSS单系统及多系统组合测速结果如图3所示,表1示出了其均值及RMS。可以看出,单系统测速时,BDS精度最低,其E、N、U方向RMS分别为38.1 mm/s、46.5 mm/s、105.4 mm/s,GLONASS在E、N方向精度略优于GPS,RMS分别为20.2 mm/s、 25.6 mm/s,而其U方向精度比GPS低,RMS为90.7 mm/s,GPS在U方向RMS为60.7 mm/s;双系统组合测速时,GPS/GLONASS测速精度最高,在E、N、U方向RMS分别为16.6 mm/s、20.8 mm/s、49.3 mm/s,BDS/GLONASS在E、N方向精度略优于GPS/BDS,但在U方向精度比GPS/BDS低,这主要是由于BDS、GLONASS单系统测速在U方向精度都比GPS低很多,导致了BDS/GLONASS在U方向精度较低,但与单系统相比,精度均有较大提高;当采用GPS/BDS/GLONASS组合时,其精度明显优于双系统,其E、N、U方向RMS分别为14.5 mm/s、17.5 mm/s、42.9 mm/s,当加入Galileo和QZSS后,E、U方向精度略微有所提高,N方向不明显。

综上,采用原始多普勒观测值测速,GPS、BDS、GLONASS单系统时E、N方向精度约为20.2～46.5 mm/s,U方向精度约为60.9～105.4 mm/s,双系统组合测速精度比任何单一系统测速精度都有所提高,多系统组合测速结果优于双系统测速结果,E、N方向精度可达到14.2 mm/s、17.5 mm/s,U方向为42.3 mm/s.

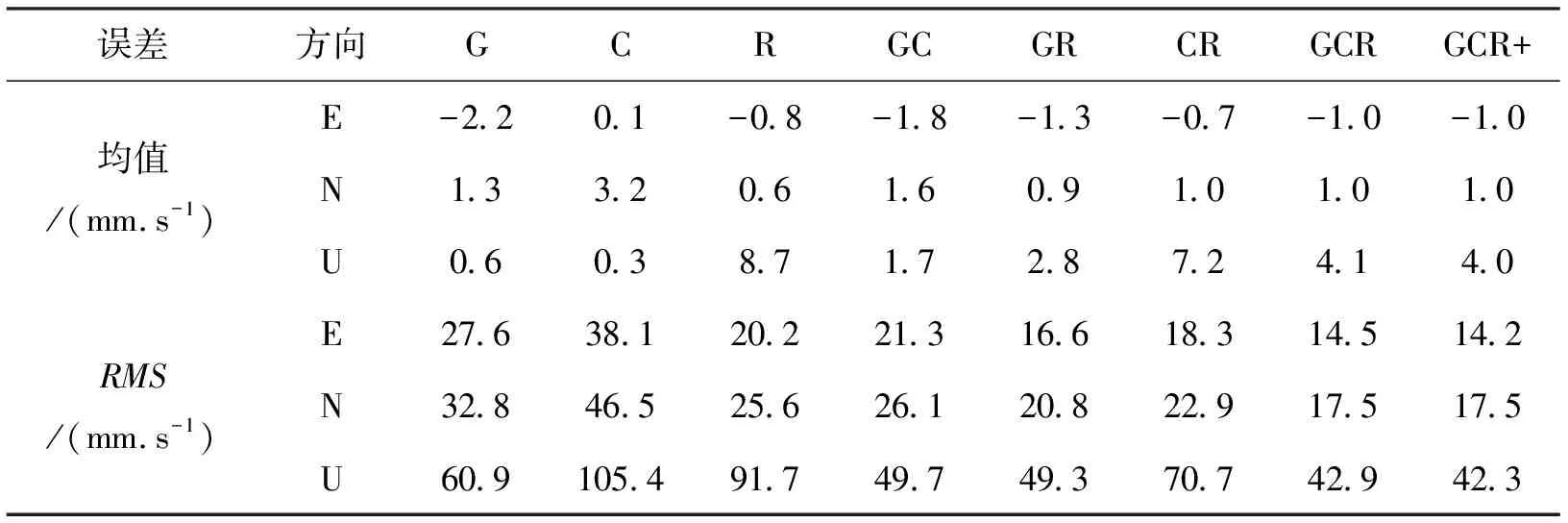
误差方向GCRGCGRCRGCRGCR+均值/(mm.s-1)E-2.20.1-0.8-1.8-1.3-0.7-1.0-1.0 N1.33.20.61.60.91.01.01.0 U0.60.38.71.72.87.24.14.0 RMS/(mm.s-1)E27.638.120.221.316.618.314.514.2 N32.846.525.626.120.822.917.517.5 U60.9105.491.749.749.370.742.942.3

2.2 导出多普勒观测值多系统GNSS测速

图4示出了基于相位一阶中心差分测速结果,其均值及RMS统计结果如表2所示。单系统测速时,BDS在E、N方向精度最低,RMS分别为4.5 mm/s、4.9 mm/s,U方向RMS也达到4.4 mm/s,但从图中可以看出,BDS在E、N、U方向都比较平滑,但由于其均值较大,导致RMS较大,即精度较高,但精确度较低,GPS、GLONASS在E方向精度相当,在N方向GLONASS优于GPS,U方向GLONASS最低,RMS为7.4 mm/s;双系统组合明显提高了测速精度,其中以GPS/GLONASS组合精度最高,其E、N、U方向RMS为0.7 mm/s、0.8 mm/s、1.9 mm/s,GPS/BDS组合测速精度最低,但其E、N、U方向精度也可到达0.9 mm/s、1.2 mm/s、3.3 mm/s;GPS/BDS/GLONASS多系统组合时,与单系统、双系统相比,明显提高了测速精度,但U方向精度比GPS/GLONASS略低,主要是因为多系统组合时U方向均值偏差较大的原因,加入Galileo、QZSS系统后,由于新增卫星数很少,精度提高并不明显。

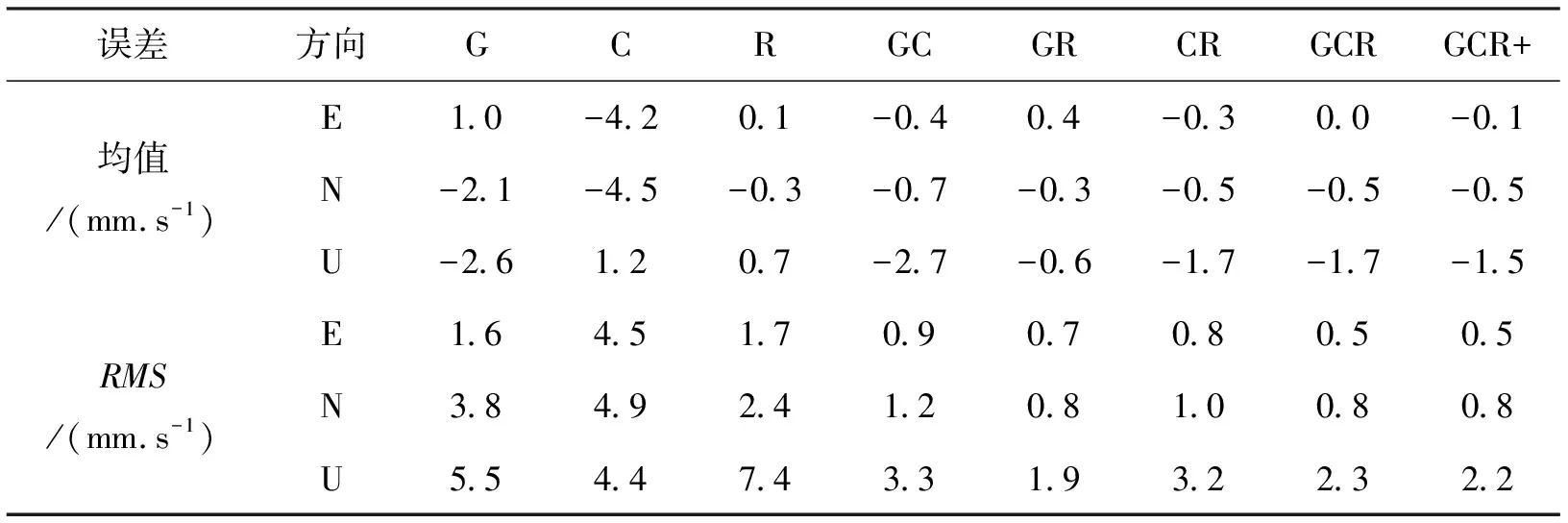
误差方向GCRGCGRCRGCRGCR+均值/(mm.s-1)E1.0-4.20.1-0.40.4-0.30.0-0.1 N-2.1-4.5-0.3-0.7-0.3-0.5-0.5-0.5 U-2.61.20.7-2.7-0.6-1.7-1.7-1.5 RMS/(mm.s-1)E1.64.51.70.90.70.80.50.5 N3.84.92.41.20.81.00.80.8 U5.54.47.43.31.93.22.32.2

2.3 原始多普勒观测值与导出多普勒观测值组合测速

图5示出了原始多普勒观测值与导出多普勒观测值组合测速结果,表3对解算结果进行了统计。将两种观测值组合测速结果与导出多普勒观测值测速结果进行比较,可以看出,GPS、GLONASS单系统时,两种观测值组合测速能够明显地提高速度解算精度,而BDS没有明显的改善,这是因为BDS导出多普勒观测值测速精度比较低,且均值存在微小偏差,而其原始多普勒测速精度也较低,组合时无法再明显提高其精度;在双系统及多系统组合时,由于导出多普勒观测值测速已经能够达到较高的精度,且原始多普勒观测值要比导出多普勒观测值精度低许多,故再加入原始多普勒观测值,无法明显提高测速精度,有时还会使测速结果受到影响而使其精度降低。即单系统时两种观测值组合能够明显提高测速精度,在多系统时效果不明显,其根本原因是因为,单系统时,在导出多普勒观测值基础上增加了一倍原始多普勒观测值,实质是大大改善了方程的结构,从而提高了测速精度;多系统组合时,导出多普勒观测值已经很多,观测方程的结构已经很好,再增加精度本来不高的原始多普勒观测值已无法明显提高测速精度,如果定权不当还会反受原始多普勒观测值的影响。

误差方向GCRGCGRCRGCRGCR+ 均值/(mm.s-1)E0.7-4.20.2-1.40.4-1.3-0.8-0.8 N-0.7-4.5-0.2-1.1-0.3-1.2-0.8-0.8 U-0.91.20.4-4-0.6-2.9-3.0-3.0 RMS/(mm.s-1)E1.34.50.81.70.71.51.01.0 N1.44.91.01.40.81.51.11.1 U2.54.43.54.41.93.93.43.4

从GNSS多系统组合的角度看,采用原始多普勒观测值与相位导出多普勒观测值组合测速时,双系统能够在一定范围内提高测速精度,如表3中GPS/GLONASS组合测速的精度比GPS、GLONASS精度高,这说明在两种观测值组合时,GNSS系统组合能够提高测速精度,GPS/BDS测速精度与BDS相比也提高了许多,但由于BDS原始多普勒测速精度较低,其精度比GPS单系统低;GNSS多系统组合时,测速精度也有一定的提高,同样由于受到BDS原始多普勒观测值的影响,使其测速精度比GLONASS、GPS/GLONASS测速精度略低,当然这里本质的原因是GLONASS、GPS/GLONASS测速精度本来就比较高,再者本文没有建立严格的随机模型,导致多系统组合时测速精度很难再得到提高。

尽管导出多普勒测速精度比原始多普勒测速精度高一个数量级,但需要注意的是,导出多普勒观测值解算的是接收机的平均速度,而原始多普勒观测值是瞬时观测量,得到的是接收机的瞬时速度。这对于静态载体或者低动态匀速载体来讲,结合高采样率的载波观测值,解算结果与载体真实速度差别不大,采样率越高,越接近载体瞬时速度;但对于高动态载体,或者速度变化较快的载体,导出多普勒法难以完全反应载体的真实速度,尤其是在速度发生变化及其相邻时刻,因为导出多普勒观测值是根据载波相位差分而来,反映的是载波相位观测值的平均变化率,这是导出多普勒与原始多普测速的根本不同。两种测速方法结合,在理论上恰好能够互补,因此,在下一步的动态测试中,将重点测试原始多普勒与导出多普勒组合时,在速度变化时刻的测速效果。当然,无论是静态还是动态,多系统组合都具有一定的优势,尤其是在遮挡环境下。

3 结束语

本文基于GNSS多普勒测速原理,结合静态数据,对GNSS单系统、双系统、多系统组合时原始多普勒测速、载波相位一阶中心差分导出多普勒测速及两种观测值组合测速进行了测试,并对测速结果进行了比较,结果表明:1) 单GNSS系统原始多普勒测速精度为厘米级每秒,相位导出多普勒测速精度为毫米每秒,多系统组合能够明显地提高原始多普勒和导出多普勒测速精度,同时能够在一定范围内提高原始多普勒与相位导出多普勒组合测速的精度;2) 单GNSS系统时,原始多普勒与导出多普勒组合能够有效地提高测速精度,多系统组合时,两种观测值组合效果不明显。同时,由于论文结论均是基于静态数据进行测试的结果,下一步将基于动态数据和不同遮挡环境的多系统GNSS数据进行测试,进一步对相关结论进行验证。