GNSS导航信号的开环补偿多径抑制方法

高科

(中国西南电子技术研究所,四川 成都 610036)

0 引 言

多径效应是指由于传输信道中存在遮挡物,使得测距信号的直达信号和散射后的复制品一起到达接收机,造成原始测距信号在幅度、相位和延迟上发生变化,进而影响测量精度。一旦多径信号相对于直达信号的延迟在正负1个码片之内,就会对伪距的测量带来较大的误差。

随着全球导航卫星系统(GNSS)的增强和现代化程度的提高,对GNSS的定位精度提出了越来越高的要求。星历误差、电离层和对流层延迟误差、卫星钟差等可以通过建立更加精确的模型和采用差分测量等措施进行减小或消除,而多径信号由于不具备空间相关性,难以通过差分方法进行消除[1],已经成为影响卫星导航测距精度的重要误差来源[2]。因此研究多径抑制方法对提高导航定位的准确性具有重要意义。

1 目前常用多径抑制方法

多径抑制主要有两类方法,一类是天线抑制多径技术[3-4],另一类是接收机处理抑制多径技术。天线抑制多径技术通过改进天线结构,使得方向图的主瓣对准测距信号的来波方向,减少对多径反射方向信号的接收。该方法通常需要已知或估计发射端的角度信息,具有一定的局限性。接收机处理抑制多径技术可以分为参量式和非参量式两类。

参量式是使用估计理论来估计多径信号的参数,然后根据估计参数修正接收信号,减小多径信号的影响。最大似然估计被认为是一种理想的多径估计方法,MEDLL算法[5]、MMT算法[6]等都采用了最大似然估计。文献[7]提出使用一组由卡尔曼滤波器控制本地码相位的相关器对接收信号的相关峰进行可变间距采样,提高了多径参数的估计精度。文献[8]在伪码解扩前通过最大似然估计方法来估计直达信号,然后通过对多路相干积分进行最优组合,得到码相位跟踪误差的最佳估计值。文献[9]提出了一种利用相关曲线偏差分离导航卫星多径信号的方法。

参量式技术虽然对多径的抑制效果较好,但是计算复杂度高;而非参量式旨在设计特殊的鉴别器,使之对多径信号不敏感,由于其计算复杂度较低,得到了广泛的应用。如窄相关技术把延迟锁定环路的早迟间隔由传统的1个伪码码片缩短到小于1个伪码码片,同时提高了接收信号的带宽,可以显著地降低多径的影响[10]。ELS技术根据存在多径信号时接收机中频信号与本地信号的相关函数两侧斜率不相等的现象,通过两组早迟相关器获得相关函数两侧的斜率,并计算出其交点,将交点所对应的横坐标作为多径误差的估计,返回给伪距计算以纠正该误差。文献[11]结合ELS技术和 BOC信号旁瓣消除技术设计了一种适合 BOC(m,n)的多径抑制技术。文献[12]中的Strobe相关器将本地信号经过特殊裁剪,使得接收机中频信号与本地信号的相关函数变窄,以构造对多径信号不敏感的鉴别器曲线。由于早迟间隔减小到一定程度后,码跟踪环路的抗多径性能提升效果受限[13],文献[14]提出了多门延迟方法来解决多径干扰问题。MGD采用多对早迟相关器构成鉴别器,其中相关器的对数、相关器的间隔和相关器的权重系数一般情况下可按照某种标准来优化选择。

2 多门延迟和曲线拟合方法

2.1 多径信号模型

接收机接收的信号由直射信号和多径信号组成,多径信号比直射信号存在延时、相移和衰落。存在多径时,接收信号r(t)的模型为

(1)

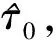
(2)

(3)

式中:R(τ)为导航信号的自相关函数; Δ为早迟门间隔。实现过程中相关输出分为同相和正交分量,不同的鉴别器结构可以获得不同的鉴别器输出。

图1中黑色圆圈线表示接收信号中的直射信号与本地伪码的相关函数,黑色星星线表示接收信号中的同相多径信号(延迟0.5个码片(chip),幅度衰减3 dB)与本地伪码的相关函数,黑色三角线表示接收到的混合信号与本地伪码的相关函数。E表示早迟码环鉴别器的早门,L表示迟门,EL间隔为1个码片,P表示早迟门鉴别器对准的伪码位置,Pm表示接收机直射信号的伪码位置。

图2与图1的说明一致,只是表示反相多径信号的情况。

2.2 多门延迟

从图1和图2可以看出,接收信号无论是存在同相多径还是反相多径,早迟鉴别器对准的伪码位置都与直射信号的伪码位置有偏差。但是直射信号的伪码位置与相关函数的峰值是一致的,因此可以通过相关函数峰值的位置来确定直射信号的伪码位置。

以码环鉴别器对准的P点为中心,增加本地相关器的个数,相关器的间隔为1个或多个系统时钟,相关器的覆盖范围为正负1个码片。接收信号与所有的本地相关器进行运算,将所有相关器的输出值进行比较,找出最大相关值对应的伪码位置,即为直射信号的伪码位置Pm.计算Pm与P点的码位置偏差CorM(chip),即为伪距补偿值。靠近E路的定义为负值,靠近L路的定义为正值。

多门延迟方法可以将伪距补偿的精度提升至1个系统时钟。

2.3 曲线拟合

另外,实际中,接收信号因受前端带宽的影响,与本地伪码的相关函数的顶部会变圆,类似于抛物线的顶部。因此,为了进一步提升多门延迟方法的精度,并考虑到相关函数受前端带宽的影响,在多门延迟得到的Pm的基础上,进一步对相关函数进行曲线拟合,得到更准确的码位置。

考虑到复杂度问题,此处的曲线拟合采用二次抛物线拟合。由于相关函数峰值附近的点对估计起到决定性的作用[15],因此选取Pm为二次抛物线估计的坐标原点。

具体方法为:以Pm为坐标原点,取Pm以及左右各2个相关器的相关函数值(共5个点)进行二次抛物线拟和,相关函数值从早到迟依次可以表示为:y1、y2、y3、y4、y5。

二次抛物线表达式为:y=ax2+bx+c。假定相关器的间隔为1/16码片,则方程组可表示为

(4)

可得抛物线的参数:

a= 18.285×(2×y1-y2-2×y3-

y4+2×y5),

b=-1.6×(2×y1+y2-y4-2×y5),

根据-b/(2a)计算出抛物线顶点Pc距离Pm的偏差CorC为

CorC=0.04375×

(5)

因此,最终的伪距补偿值Cor为两部分偏差之和,即,Cor=CorM+CorC.

2.4 开环补偿

本方法不改变接收机跟踪环路中码环鉴别器的早迟间隔,只是通过多门延迟和曲线拟合找出直射路径的伪码位置和码环鉴别器P路之间的偏差,将其作为伪距测量的误差值补偿给伪距计算。

3 仿真实验

为了仿真此方法的性能,本节对比了三种环路鉴别方法的同相多径和反相多径的误差包络值,这三种方法分别是早迟(EL)间隔1 chip的常规环路鉴别器、早迟间隔0.5 chip的窄相关鉴别器以及利用多门延迟和曲线拟合对伪码位置进行补偿的新方法。参与测试的是GPS导航系统的1号卫星,在接收信号直射路径上分别加上幅度衰减3 dB的0°同相多径信号和180°反相多径信号,接收信号经过带宽为2 MHz的射频前端处理和滤波后,与本地中频信号进行相关,并进入环路滤波器进行相位和频率以及伪码位置的锁定。多径时延的测试范围为0～1.5 chip,系统时钟频率为16.368 MHz,中频频点为4.092 MHz.性能测试结果如图3所示。

图中圆圈和正方形图标分别表示早迟间隔为1 chip的鉴别器的同相和反相多径误差的包络线,加号和乘号图标分别表示早迟间隔为0.5 chip的鉴别器的同相和反相多径误差的包络线,星星和菱形图标分别表示在早迟间隔为0.5 chip鉴别器的基础上加上伪码位置补偿后的同相和反相多径误差的包络线。

从图中可以看出,早迟间隔变小后,可以降低一部分伪码误差,但仍然有较大的残留,且对短多径的效果有限。进一步使用多门延迟和曲线拟合补偿后的伪码误差大大降低,且对短、中、长多径都有较好的抑制效果。

4 结束语

本文详细描述了一种基于多门延迟和曲线拟合的多径抑制方法,包括抑制原理、实现方法和仿真性能。计算机仿真结果表明,此多径抑制算法对短、中、长多径都可以达到很好的抑制性能。且此方法对前端带宽不敏感,可以在较窄的前端带宽下取得良好的多径抑制效果。由于是开环补偿,没有改变正常的环路跟踪参数,因此环路的抗动态性能可以得到很好的保持。

另外,在具体的工程实现中,为了节约资源,可以将多门延迟增加的码相关器的覆盖范围降低。考虑到码环鉴别器的跟踪误差和曲线拟合需要的范围,可以将正负1 chip减小至正负0.5 chip.