用于GNSS信号的可变相干积累时长的时频域结合捕获算法

田野,湛剑佳

(湖南广播电视大学,湖南 长沙 410004)

0 引 言

随着全球卫星导航系统(GNSS)的发展,导航接收机的应用越来越广泛,由于导航信号到达地面时的信号功率较小,通常低于-160 dBW[1],因此对导航信号的捕获和接收处理需要采用较高性能的捕获算法。为了提高对导航信号的捕获概率,导航接收机通常会采用相干积累和非相干积累相结合的方法。

由于存在多普勒频移,卫星信号的检测本质上是一个时间-频率的二维搜索问题。传统的接收机往往采用并行搜索结构,以加快搜索速度。文献[2-7]对时域并行、频域并行、时频域结合的算法进行广泛的研究。其中时频域结合的搜索算法采用分段相关和FFT频域并行搜索相结合的方法,可以将时间-频率的二维搜索近似为一维时间搜索,易于硬件采用流水结构实现[8-11]。但该方法存在设计参数给定后,信号的相干积累时长不易调节的缺点。当接收机需要捕获的信号较强时,可以采用较短的相干积累时长,快速完成信号的捕获;当接收机需要捕获的信号较弱时,需要采用较长的相干积累时长,以便捕获到更弱的导航信号。采用时频域结合的捕获算法,存在信号相干积累时长不能灵活调整的不足,为此,本文设计了一种可变相干积累时长的捕获算法,在捕获电路结构基本不变的基础上,可以延长信号的相干积累时长,同时不引入额外的多普勒损耗,以获得更好的捕获性能。

本文第一部分从信号的捕获模型入手,描述了传统时频域捕获算法,并设计了一种可变相干积累时长的捕获算法,该方法在延长相干积累时间的同时,也等效提高了FFT运算的点数,第二部分对比分析了可变相干积累时长的FFT损耗和检波损耗,指出了延长相干积分时间不会增加额外的FFT损耗,但可以减小检波损耗,最后通过蒙特卡洛仿真验证了可变相干积累时长捕获算法的正确性和有效性。

1 信号捕获模型

待捕获的GNSS导航信号可表示为

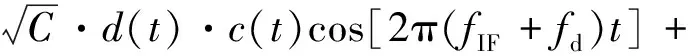
n(t),

(1)

式中:C为信号的功率;d(t)为导航电文;c(t)为伪随机码;n(t)为高斯白噪声,双边带谱密度N0.C/N0为信号的载噪比,单位dBHz.接收信号经正交下变频和低通滤波器处理后,得到信号捕获处理的基带复信号,其表达式为

(2)

由于信号的捕获是通过大量相关器实现的,为了行文方便,将信号捕获过程中所用的相关器如图1所示的方式进行编号,共有M×N个相关器。每个相关器实现对IQ两个支路的信号进行相关,如图1所示,第n行m列相关器输出的相关结果可表示为

xn,m=In,m+jQn,m=C/N0·Tc·sinc(πfdTc)·

R(Δτ)·ej·(2πfdiTc+Δθ)+nw,

(3)

式中:Tc为相干积分时间; sinc(πfdTc)为信号多普勒的大小对的短时相关积累结果的影响;R()为伪码自相关函数,忽略码相位损耗有R(Δτ)=R(0)=1;i=nM+m,n=0,1,…,N-1,m=0,1,…,M-1; Δθ为残余相位;nw为复噪声信号。

1.1 传统时频域结合捕获算法

传统时频域结合方法的结构如图2所示。

根据上述结构,每个FFT组的结果为

(4)

(5)

式中,F表示FFT的点数。通过FFT运算,实现了对信号的频域搜索,频率分格大小为1/(F·Tc)。经过FFT运算后,信号的相干积分时间变为了m·Tc.

当信号的多普勒频率变化在信号捕获的过程中可以忽略的条件下,不同FFT组相同序数的结果存在如下关系

Xn1,k=Xn2,k·ej·2π·fd·(n1-n2)·Tc.

(6)

为了消除不同组FFT结果间的相位差异,需要对不同组FFT的结果进行非相干累加处理,一种常用的非相干累加方式为包络累加,具体有

(7)

式中,下标k为多普勒的搜索格子。上述过程仅仅完成了一个时延处的搜索,如果用下标τ表示时延的搜索格子,则最终的捕获判决量可设计为取所有时间-频率搜索格子内的最大值即

(8)

当V大于门限时,则认为捕获到信号,否则认为捕获失败。

在时频域结合的捕获算法中,当相关器的积分时间Tc和输入FFT的相关结果个数M确定后,整个算法的相干积分时间也就固定了。为了能够延长信号的相干积分时间,进一步提升接收机对弱信号的捕获性能,本文设计了一种可变相干积累时长的捕获算法。

1.2 可变相干积累时长的捕获算法

在时频结合的捕获算法中,信号的相干积累时长为由相关器的积分时间Tc和输入FFT的相关值点数M决定,如果要延长相干积累时长,可以增加输入FFT的点数M.在保证捕获结构基本不变的基础上,可以对M进行成倍的增加,即将M变为L·M.当输入FFT的点数增加后,如果不增加FFT的点数,将会导致FFT损耗的增大,为了不引入额外的损耗,需要同时增加FFT的点数,考虑到FFT的运算特点,一种简单的实现方式是将L设计为2的整数次幂,这样可以利用原有的F点FFT,实现L·F点的FFT.当L=2时,可变相干积累时长的捕获算法可以设计为图3所示的结构。

如图3所示,可以将相邻两组相关器按图中所示编号重新排列,分别记为0到2M-1,相关值为xm,m=0,1,…,M-1.信号的相干积累时间的延长方式是通过等效实现对2M点相关结果的2F点的FFT实现的,这样信号的相干积累时间就从M·Tc增加到了2M·Tc.为了等效实现2M点相关结果的2F点FFT运算,需要对两个F点的FFT的运算结果进行组合加权,具体算法如表1所示。

表1 L=2时可变相干积累时长的捕获算法描述

上述过程借助于FFT运算的特点,利用2个FFT运算单元,等效地实现了2F点的FFT运算,这样,在延长信号相干积累时长的同时,也提高了FFT的点数。依次类推,也可以将信号的相干积累时长延长至原来的4倍甚至更高,但带来的代价是增加了组合加权过程。本文主要以L=2为例,对算法的性能进行分析。

对图3中的组合加权结果Yk,l进行包络检波,并进行N/2次后积累,可得到一个时延-多普勒格子处的检测量,即

(9)

算法后续的处理过程和传统的时频域结合捕获算法保持一致。在可变相干积累时长的算法中,相干积累时长的改变通过调整参数L实现,即当L=1时,该算法等价为传统的时频结合捕获算法,当L>1时,该算法的相干积分时间增加到了L·M·Tc.

2 性能分析

2.1 FFT损耗分析

在进行FFT运算的过程中,相当于对信号的频域进行搜索,经过FFT处理后,信号的相干积分时间等价于M·Tc,由于FFT运算过程中不可避免地会产生栅瓣效应,因此,会引入损耗,经过FFT处理后,获得的增益大小为[3-4]

(10)

式中,k为FFT最大值对应的谱线序列,定义FFT损耗Ls为

(11)

式中:G0为FFT运算中不考虑栅瓣效应的理想增益,即为输入FFT的数据段数M.在可变相干积累时长的捕获算法中,FFT的点数由F点变为了L·F点,输入FFT的数据段数由M段变为了L·M段,因此,FFT带来的增益和FFT损耗分别为

(12)

(13)

当L=1时,可变相干积累时长的捕获算法退化为传统的时频域结合的捕获算法。图4示出了两种算法下的FFT损耗结果,其中L=1对应传统捕获算法,L=2对应延长一倍相干积累时长的算法。仿真中所用参数为Tc=0.05 ms,M=20,FFT点数为32点。遍历了多普勒从0到5 000 Hz下的FFT损耗,可以看出,延长相干积分时间后,基本上不影响FFT损耗。

2.2 检波损耗

为了实现对FFT结果的非相干积累,通常采用包络检波的方式对FFT的运算结果进行检波处理,然后再进行非相干积累。包络检波过程会引入额外的检波损耗Cs,具体大小为[12-13]

(14)

其中,SNRB为送入包络检波器的信号信噪比。

从损耗公式可以看出,检波前信噪比SNRB越大,包络检波损耗越小。显然对于可变相干积累时长的捕获算法,当相干积分时间增加为原来的L倍后,检波前的信噪比也会增加至原来的L倍,因此其检波损耗为

(15)

显然L=2时的检波损耗比L=1时的检波损耗小,图5示出了两种参数下检波损耗随SNRB的变化关系,上图显示了L=2和L=1时的具体检波损耗,下图给出了L=1和L=2时检波损耗的差值。可以看出,延长一倍相干积分时间,检波损耗可以减小0.8～3 dB,检波前信噪比越小,检波损耗的减小量越大。

通过2.1节和2.2节的分析,可以看出,采用可变长相干积累时长的捕获算法,虽然不会降低FFT损耗,但通过延长相干积分时间,能够提升检波前的信噪比,降低检波损耗,提升检测性能。

2.3 算法计算负荷分析

对比图2和图3,以L=2时的可变相干积分时长的算法为例,相比传统的时频域结合捕获算法,对于可变相干积分时长的算法,根据表1中步骤3和步骤4可以看出,该算法需要额外增加N·F个乘法器和N·F个加法器,以实现延长一倍相干积分时长的效果。除此之外,为了实现将两个F点FFT的结果拼接成一个2F点FFT的结果,还需要增加表1中步骤1和步骤2所需要的逻辑控制部分,以实现对缓存数据的奇偶序号提取,这在传统时频域结合的捕获算法中是不需要的。综合上面两个方面的因素,可变相干积分时长的捕获算法是以增加计算的负荷和实现复杂度为代价实现捕获性能的提升。

3 性能仿真验证

采用GPS-L1C/A信号进行仿真,仿真信号条件设置如表 2所示,总的信号积累时长为4 ms,信号的时延搜索范围为一个伪码周期,即1 ms,分别仿真L=1和L=2两种情况下捕获算法的性能。

表2 仿真条件下信号的捕获参数设置

仿真实验采用蒙特卡洛的仿真方法,主要通过对比不同捕获算法在不同条件下的捕获概率和虚警概率指标[1]。捕获判决方式采用取大判决和过门限判决相结合的方式[6],即取一次时频域结合算法中得到所有的捕获分格下的最大值作为判决量,并将该最大值和门限进行比较,如果比门限高,则认为捕获成功,否则捕获失败。下面对比了两种算法在不同信号强度和不同多普勒条件下的性能。

3.1 不同信号强度下的捕获性能

为了对比两组参数在不同信号强度下的捕获性能,设置信号多普勒参数固定为500 Hz,此时仿真载噪比从30 dB·Hz到45 dB·Hz下的捕获性能。图6示出了虚警概率为1×10-3条件下,两种算法的捕获概率随信号载噪比的变化关系,可以看出,将采用可变相干积分时间的捕获算法,将相干积分时间延长一倍,可以提升约1 dB左右的捕获性能。图7示出了当信号强度为37 dB·Hz时,两种捕获算法在不同虚警概率下的捕获性能,可以看出当虚警概率为0.1时,延长一倍的积分时间,可以提升约10%左右的捕获概率。

3.2 不同多普勒条件下的捕获性能

对比信号多普勒对可变相干积累时长的影响,分别仿真不同多普勒初值下L=1和L=2两组参数的算法性能,多普勒初值从0～5 000 Hz,以500 Hz为步进量进行遍历,信号强度设置为37 dB·Hz,两种算法的结果如图8所示。

从上面的仿真结果可以看出,延长相干积分时长后,信号多普勒从0变化到5 000 Hz时,其捕获概率均大于传统时频域结合的捕获算法,这也说明了本文所提出的方法并不会引入额外的多普勒损耗。另外,两种方法下,其捕获性能均随着信号多普勒的增大而下降,这主要是由于信号多普勒越大,如式(3)所示,在短时相关长度Tc固定的条件下,相关器输出结果中的多普勒损耗越大,从而导致算法性能的下降。

3.3 算法计算负荷仿真

为了验证可变相干积分时长算法的计算负荷,采用Matlab软件,分别统计该算法和传统时频域相结合算法的计算耗时,用来等效地对比两种算法的计算负荷。如果matlab计算的耗时越小,则说明算法的计算负荷越小。由于实际的捕获算法可能由不同的器件或平台实现,因此本节的计算负荷仿真只能定性地对两种方法的计算负荷进行验证。表3示出了两种算法在不同次数下的仿真耗时。

表3Matlab下算法运行耗时结果s

L100次1000次 L=160.10593.69 L=271.15673.28

根据上面的结果可以看出,L=2时的可变相干积分时长的捕获算法运行耗时明显比传统时频域相结合的算法计算耗时长,这就表明该算法的计算负荷较大,从而验证了2.3节的分析结论,这也说明了可变相干积分时长的捕获算法是以增加算法的计算负荷为代价提升捕获性能的。

4 结束语

本文提出了一种可变相干积累时长的时频域结合捕获算法,在延长信号相干积累时间的同时,可以等效提高算法中FFT的运算点数,保证在减小算法检波损耗的同时,不增加额外的FFT损耗。分析和仿真表明,采用可变相干积累时长的算法,通过延长信号的相干积累时间,可以提升信号的捕获性能,但带来的代价是增加了算法的计算负荷。