高速水润滑止推轴承的滑移润滑性能研究
2018-10-08汪双华曾良才吴振鹏湛从昌
汪双华,曾良才,吴振鹏,湛从昌
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081; 2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081)
水润滑轴承具有剪切阻力小、冷却效果好、污染少等优点,故而在中高速止推轴承领域有着广阔的应用前景。但作为润滑剂的水本身黏度低、动压润滑性能较差,因此从推力瓦设计层面入手提高轴承润滑性能的方法受到了越来越多的关注。近年来,采用微织构化表面、改善瓦面粗糙度、曲面化推力瓦等方式来提高止推轴承动压润滑性能的技术已得到广泛应用[1-2]。此外,随着各种新型疏水材料与润滑剂的深度推广,使得流体与固体表面存在一定的相对滑移速度,构成了相应的边界滑移条件[3]。滑移/非滑移表面已经在管道减阻、机械密封、人工关节等领域获得初步应用[4],因此在引入滑移/非滑移异质界面的条件下,研究轴承的动压润滑性能具有一定的实用价值。由于经典Reynolds方程不再适用于滑移/非滑移异质界面,因此Spikes[5-6]建立了扩展形式的Reynolds方程,并证明了“半湿润性”轴承具有较好的润滑性能。Aurelian等[7]也通过研究指出,合理分布滑移/非滑移异质表面区域在提高轴承的承载能力方面具有与织构相似的作用效果。Salant[8]等研究了滑移/非滑移异质界面沿径向分布时滑动轴承的动压润滑性能及其机理。这些研究表明,在推力瓦不同区域合理分布具有滑移特性的表面,可以在减小摩擦阻力的同时增大其承载力。
目前在高速水动压润滑止推轴承的研究领域,针对滑移/非滑移异质界面的文献报道相对欠缺,相关理论也有待完善。因此本文基于边界滑移条件,将滑移/非滑移异质界面引入轴承推力瓦模型,采用MATLAB软件对其进行仿真计算,研究其压力分布,以承载力和摩擦因数为优化目标,对比不同滑移区域分布条件下推力瓦的动压润滑性能以确定其润滑性能最优时的相关滑移参数。
1 研究模型的建立
1.1 推力瓦的几何模型
图1所示为目前主流可倾瓦块止推轴承的结构,通常由多个能在支点上自由倾斜的扇形瓦块组成,其瓦块能随着转速、载荷及轴承温度的不同而自由摆动,在轴颈周围形成多油楔,具有较高的稳定性。
本文选取止推轴承单个推力瓦片作为研究对象,将其简化为有支点、有厚度且倾斜的扇形几何模型如图2所示。图2中:r0为推力瓦内半径;r1为推力瓦外半径;θ为推力瓦扇面任意一点到瓦面边缘的夹角;ω为止推轴承的转速;h0为倾斜推力瓦最高点处与止推盘之间的水膜厚度;h为瓦面任意一点的水膜厚度;φ为推力瓦倾斜角度。

图1 可倾瓦块止推轴承
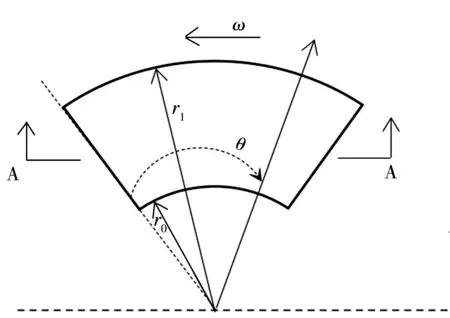

图2 推力瓦几何模型
1.2 考虑边界滑移的Reynolds扩展方程
基于文献[9]的基本假设条件,假设靠近推力瓦面滑移区域的水速不一定等于瓦面转动速度,对图2所示推力瓦创建柱坐标系,采用微元体分析方法进行公式推导,得到水膜中任意一点处水流的周向速度u及径向速度v的计算公式分别为:

(1)
(2)
在式(1)和式(2)中:p为水膜压力;u0、v0分别为推力瓦表面周向及径向滑移速度;η为水的动力黏度(25 ℃条件下);z为流场内任意一点的高度;r为该点对应的半径。
将式(1)和式(2)在膜厚方向积分,可求得沿周向和径向的体积流量qθ、qr分别为:

(3)
(4)
根据流体连续性条件,有如下方程:
(5)
将方程(3)、(4)带入方程(5)联立可得Reynolds扩展方程:
(6)
将式(6)中各参数进行无量纲化处理:


(7)
其中:

式中:p0为1个标准大气压;θ0为整块推力瓦扇面角度。
考虑边界滑移效应及边界滑移条件,推力瓦表面的周向滑移速度u0和径向滑移速度v0可以表示为[10]:
(8)
(9)

将式(1)、(2)分别代入式(8)、(9)可得:
(10)
(11)
1.3 膜厚方程
由图2可见,推力瓦承载能力主要依赖其沿周向速度方向的倾斜程度,基于此种考虑,则瓦面上任意一点的水膜厚度控制方程为:
hr,θ=h0+rsin(θ0-θ)sinφ
(12)
其中:θ=0~θ0。
1.4 推力瓦润滑特性参数
推力瓦承载力计算公式为:
θ
(13)
推力瓦摩擦力的计算公式为:

(14)
推力瓦摩擦因数计算公式为:
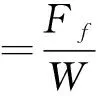
(15)
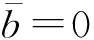

(a) W-A (b) W-B

(c) W-C (d) W-D
图3具有不同滑移区域分布的推力瓦
Fig.3Thrustpadswithdifferentslippagedistributions
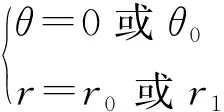
(16)
1.5 仿真求解
采用松弛迭代法[11],根据流体动压润滑膜厚范围[9]以及文献[12]总结的诸多合理边界条件、滑移长度范围选取初始仿真参数如表1所示。松弛迭代方程为:
Pk+1=Pk+β(Pk+1-Pk)
(17)
式中:k为迭代次数;β为松弛因子,一般取值0.7~1。
若上述方程的迭代收敛因子为ε,则设收敛条件为:

(18)
利用MATLAB软件对止推盘和推力瓦之间的流场进行仿真模拟。用正方形等间距网格将扇面求解区域划分为若干单元,将每个节点压力值构成的各阶差商值近似替代Reynolds扩展方程中的导数,从而将二阶偏微分方程离散化为一组代数方程,求解出节点上的离散压力分布值,获得水膜厚度分布和流场中的压力分布,再利用相关的数值积分,进一步求解推力瓦的承载力W、摩擦力Ff以及摩擦因数μ。

表1 初始仿真参数
2 结果与讨论
2.1 不同滑移区域分布条件下轴承的动压润滑性能
推力瓦模型中的水膜厚度分布如图4所示。推力瓦面的几何参数是影响膜厚分布的主要因素,因此图4中水膜厚度表现为沿瓦片倾斜方向呈线性变化。
图5所示为不同类型推力瓦表面的压力分布状况。从图5中可以看出,具有不同滑移区域分布的推力瓦表面均能产生动压,这是因为水膜厚度沿周向和径向都呈线性变化分布,水在流场中从大口流向小口,形成收敛间隙,当水流过收敛间隙时必将产生正向压力。四种类型推力瓦表面的压力分布也大致相同,其中W-A、W-B和W-D的压力峰值出现在水膜厚度最小处附近,而W-C的压力峰值出现在其滑移/非滑移区域分界处且瓦面压力值明显大于其它三组相应值。而相较于无滑移分布的W-A,W-B由于采取全滑移区域分布方式,导致其压力峰值进一步移向膜厚最小处,但峰值大小略有下降;W-D的滑移分布区域虽然也存在滑移/非滑移交界,但由于其滑移区域沿径向分布,而水流却是沿周向运动,因此这种滑移区域分布方式对推力瓦面整体压力的影响较小,几乎可以忽略不计。

图4 水膜厚度分布

(a)W-A (b)W-B
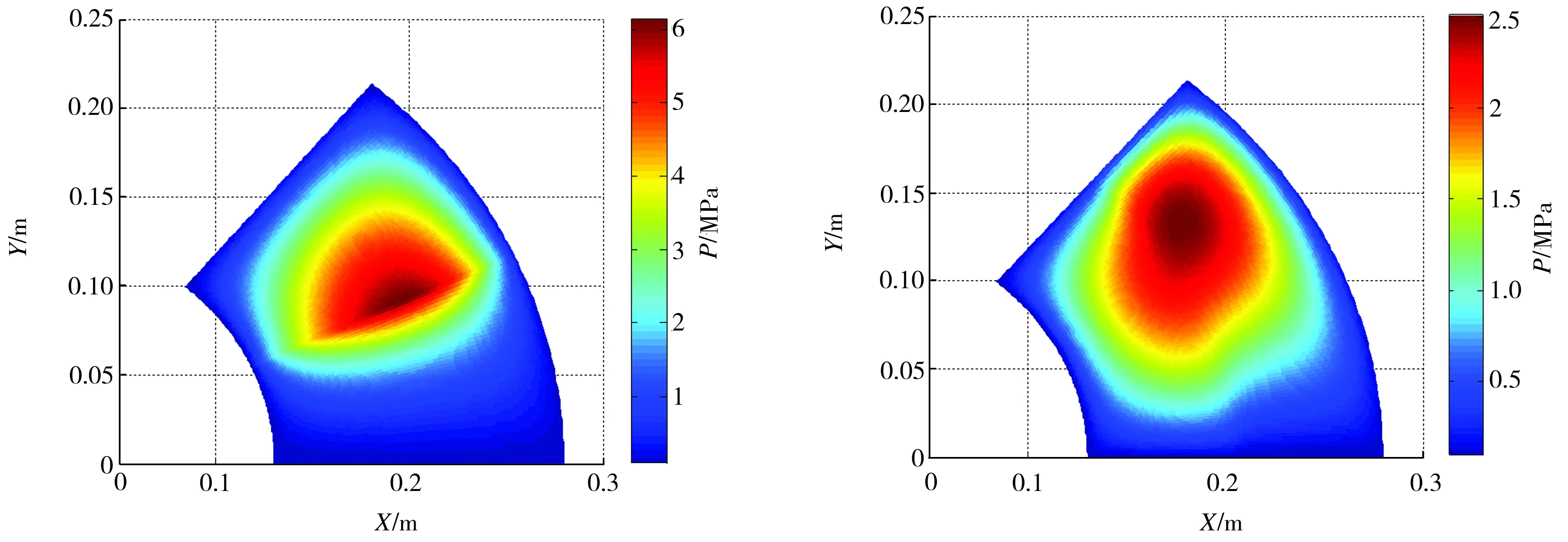
(c)W-C (d)W-D
图5推力瓦压力分布
Fig.5Pressuredistributionofthrustpads
不同类型推力瓦的承载力计算结果如图6所示。从图6中可以看出,相对于无滑移区域分布的W-A,滑移区域沿周向分布的W-C的承载力显著提高了47.96%,而W-B和W-D的相应值却分别下降了28.73%和17.40%,由此可见,W-C的滑移区域分布方式能够明显提升推力瓦的承载能力。

图6 推力瓦的承载力
不同类型推力瓦的摩擦力计算结果如图7所示。从图7中可以看出,W-B、W-C及W-D的表面摩擦力相比无滑移区域分布的W-A的相应值分别减少了6.13%、3.30%及3.97%。由此可见,将滑移区域分布在推力瓦面具有良好的减摩作用,并且推力瓦面分布的滑移区域面积越大,相应的减摩效果越明显。
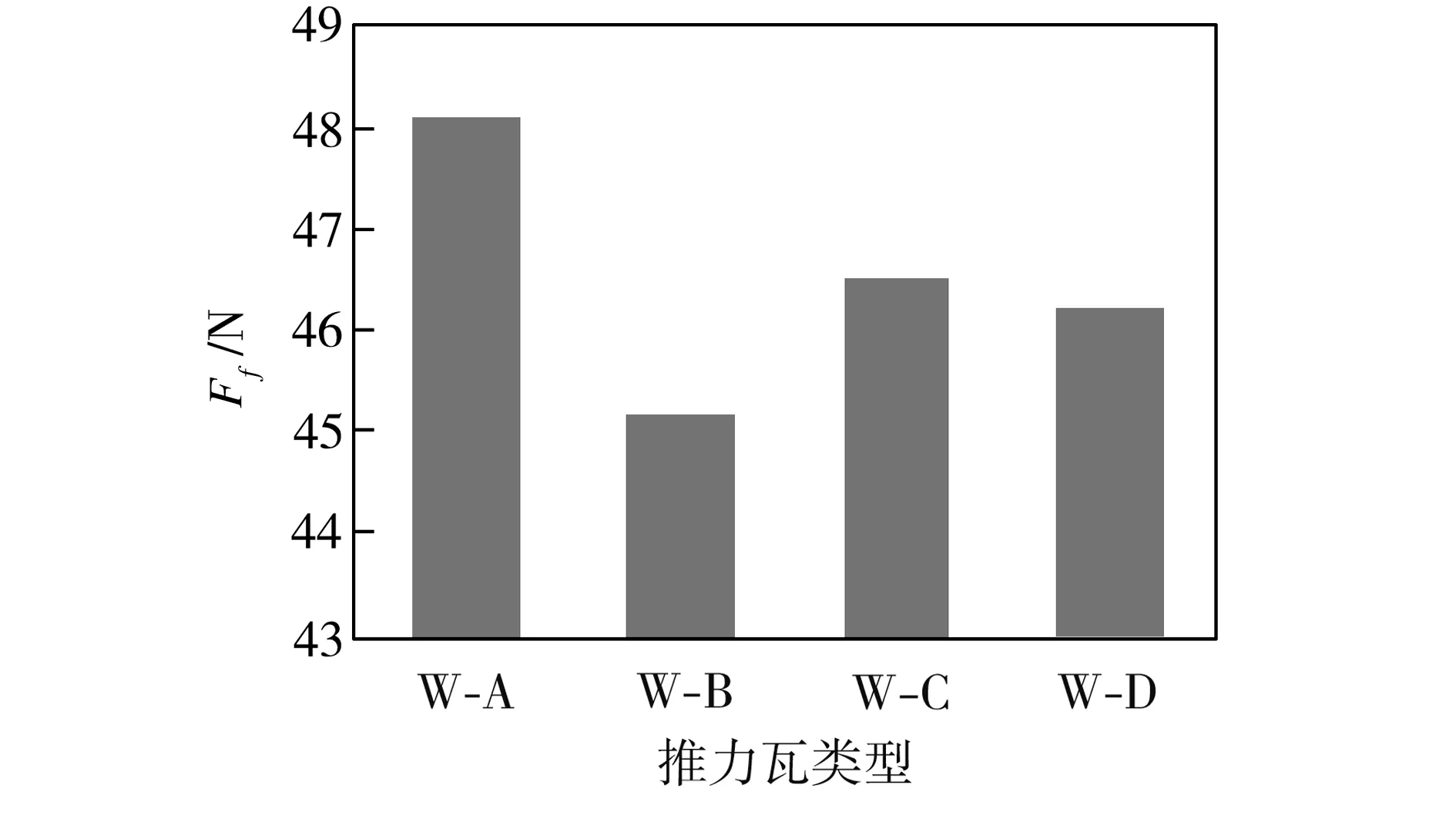
图7 推力瓦的摩擦力
不同类型推力瓦的摩擦因数计算结果如图8所示。从图8中可以看出,W-C的摩擦因数较W-A相应值下降了34.62%,而W-B和W-D的摩擦因数相比后者却分别增加了30.77%和15.38%,这应归因于W-B和W-D的瓦面承载力相对较低,由此可见W-C的滑移区域分布方式能显著减小推力瓦面的摩擦因数。
综合分析表明,当推力瓦面沿周向分布滑移区域时,可对推力瓦的承载力和摩擦因数起到较好的优化作用,这是因为滑移区域分布在水流入口一侧,产生的滑移速度与轴承转动速度方向一致,所以提高了入口一侧的水流量;在出口一侧无滑移区域分布,滑移速度为0,此处水流量不受影响。正是这种流量的变化导致压力的增加,最终新的压力分布产生压力流量使得流场总的流量达到守恒。

图8 推力瓦的摩擦因数
2.2 滑移/非滑移异质界面对不同转速条件下的轴承动压润滑性能的影响
选取W-A(b=0)、W-C(b=500 nm)为研究对象,其余参数不变,在不同转速条件下推力瓦的承载力变化如图9所示。从图9中可以看出,随着转速的增大,W-A与W-C的承载力均呈线性增长,并且增幅较大。这是因为转速的增大引起流场间的水膜厚度增大,从而提高了推力瓦的承载力。此外,具有滑移/非滑移区域分布的W-C在不同转速条件下的承载力均大于W-A相应值。在不同转速条件下推力瓦的摩擦因数变化如图10所示。从图10中可以看出,W-C的摩擦因数随转速的增大而缓慢增大,但W-A相应值却几乎稳定不变,这是因为两种推力瓦的承载力和所受摩擦力均随转速增大而增大,且W-C的摩擦力相比其承载力增幅更大,因此其摩擦因数变化明显,而W-A的承载力与摩擦力随转速增大按相同比例增加,故其摩擦因数无显著改变。此外,具有滑移/非滑移区域分布的推力瓦W-C在不同转速条件下的摩擦因数均比W-A相应值小,推力瓦W-C始终表现出比普通推力瓦W-A更佳的动压润滑性能。

图9 不同转速条件下的推力瓦承载力

图10 不同转速条件下的推力瓦摩擦因数
Fig.10Frictioncoefficientofthrustpadsatdifferentspeeds
2.3 不同滑移区域面积占比和滑移长度条件下的推力瓦动压润滑性能
以W-C为研究对象,当b分别为200、500、800、1000 nm时,推力瓦承载力和摩擦因数随其瓦面分布的滑移区域面积占比变化的曲线分别如图11、图12所示。由图11、图12可知,随着滑移区域面积占比的增大,推力瓦承载力整体呈现先增大后减小的变化趋势,而其摩擦因数相应变化趋势刚好相反。由计算分析可知,当瓦面分布的滑移区域面积占推力瓦面面积比介于0.3~0.4时,推力瓦承载力最大、瓦面摩擦力最小。此外,随着滑移长度的不断增大,推力瓦承载力和摩擦因数分别表现出递增和递减的变化趋势,并且当滑移区域面积占推力瓦面面积比介于0.3~0.4时,这种由滑移长度变化所造成的递增与递减趋势尤为明显。随着滑移区域面积占比的不断增大,具有不同滑移长度的推力瓦之间的承载力和摩擦因数的数值差距逐渐减小,当滑移区域面积占推力瓦面面积比大于0.7时,滑移长度的变化对推力瓦承载力和摩擦因数的影响几乎可以忽略不计。综合分析可知,当滑移区域面积占整个推力瓦面面积比介于0.3~0.4且滑移长度为1000 nm时,推力瓦面具有最优的动压润滑性能。

图11 不同滑移区域面积占比的推力瓦承载力
Fig.11Bearingcapacityofthrustpadswithdifferentsliparearatios

图12 不同滑移区域面积占比的推力瓦的摩擦因数
Fig.12Frictioncoefficientofthrustpadswithdifferentsliparearatios
3 结论
(1)在止推轴承推力瓦表面分布不同类型的滑移区域,均对瓦片的压力分布产生影响,尤其在靠近流场入口处沿周向分布滑移区域时,能明显增加推力瓦面压力大小,且在滑移/非滑移交界处存在压力峰值。
(2)对于不同转速条件下的止推轴承,沿周向分布滑移/非滑移异质界面能显著提高轴承推力瓦的承载力,降低其摩擦因数,使其表现出良好的动压润滑性能。
(3)当沿周向分布的滑移区域面积占推力瓦面面积比介于0.3~0.4且滑移长度为1000 nm时,轴承推力瓦具有最优的动压润滑性能。
