叠加式压电陶瓷智能骨料特性仿真研究
2018-10-08周明乐李友荣鲁光涛宋钢兵
周明乐,李友荣,鲁光涛,王 涛,宋钢兵
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081; 2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北 武汉,430081; 3.休斯顿大学智能材料与结构实验室,美国 休斯顿,TX 77204)
2007年,Song等[1]创造性地提出将压电陶瓷封装到水泥结构中组成一种新型的压电陶瓷传感器——智能骨料(smart aggregate, SA),将其预埋到被监测的混凝土结构中,在一定程度上可以克服压电陶瓷质地较脆的缺点,延长压电陶瓷的在役时间。针对上述第一代智能骨料在固化过程中易产生裂纹、无法施加预紧力等问题,Wang等[2]又开发设计了采用大理石替代水泥保护层的第二代智能骨料。为了掌握智能骨料的机电输出特性,研究人员重点对智能骨料的关键部分——压电陶瓷的基本特性进行了深入探讨,其中往往将压电陶瓷结构的运动简化为单一的轴向振动。Piao等[3-4]采用理论分析与仿真相结合的方法研究了圆形压电陶瓷径向和轴向的振动特性,结果显示其径向为低频振动、轴向为高频振动,当结构模型轴向厚度达到一定程度后,径向振动可以被忽略。Wang等[5]推导出圆形压电陶瓷叠加结构的轴向振动模型并分析了叠加型压电陶瓷整体输出性能,证明了当多片压电陶瓷叠加时,其片与片之间的轴向间隔控制在某一个范围内可以使整体结构有更好的电压或位移输出。Han等[6]建立了双片压电陶瓷智能骨料的理论模型并重点研究了该智能骨料的谐振频率及其影响因素。阎石等[7]研究了智能骨料的抗压抗剪性能,认为压电材料占整个骨料结构的比重越低,则智能骨料的抗压抗剪能力越强。
目前,国内外虽然在智能骨料结构设计、压电陶瓷自身特性及智能骨料整体特性等方面取得了一定的研究成果,但对于多片叠加式压电陶瓷智能骨料的应用研究还较少。因此,本文设计了一种将多个压电陶瓷片封装于保护结构内部的新型叠加式压电陶瓷智能骨料,并基于一维压电弹性理论方程,分析压电陶瓷的数量、厚度、叠加方式(即电学连接方式)等对智能骨料输出电压、位移、谐振频率及机电耦合系数等特性参数的影响,以期为智能骨料的制作提供参考。
1 智能骨料基本结构及理论模型
1.1 智能骨料的基本结构
如图1所示,智能骨料主要由压电层、电极层、金属屏蔽层和水泥保护层组成,其中,压电层是由多片压电陶瓷叠加在一起构成的,电极层用于引出压电陶瓷的正负极,金属屏蔽层是由铜质圆桶和桶盖构成的一个封闭式屏蔽铜壳,水泥保护层由水泥直接浇筑而成。

(a)结构装配图 (b)结构爆炸图
图1智能骨料结构示意图
Fig.1Structuraldiagramsofsmartaggregate
1.2 智能骨料的理论模型
为了便于分析,对上述智能骨料结构进行简化,如图2所示,简化后的智能骨料模型由n个压电层、n-1个电极层、2个金属屏蔽层和2个水泥保护层组成,每个压电层和电极层的厚度分别为(H2i+1-H2i)和(H2i-H2i-1),上、下金属屏蔽层厚度分别为(H2n+2-H2n+1)与(H1-H0),上、下水泥保护层的厚度分别为(H2n+3-H2n+2)与H0。智能骨料内压电陶瓷的电学连接方式有串联和并联两种,如图3所示。
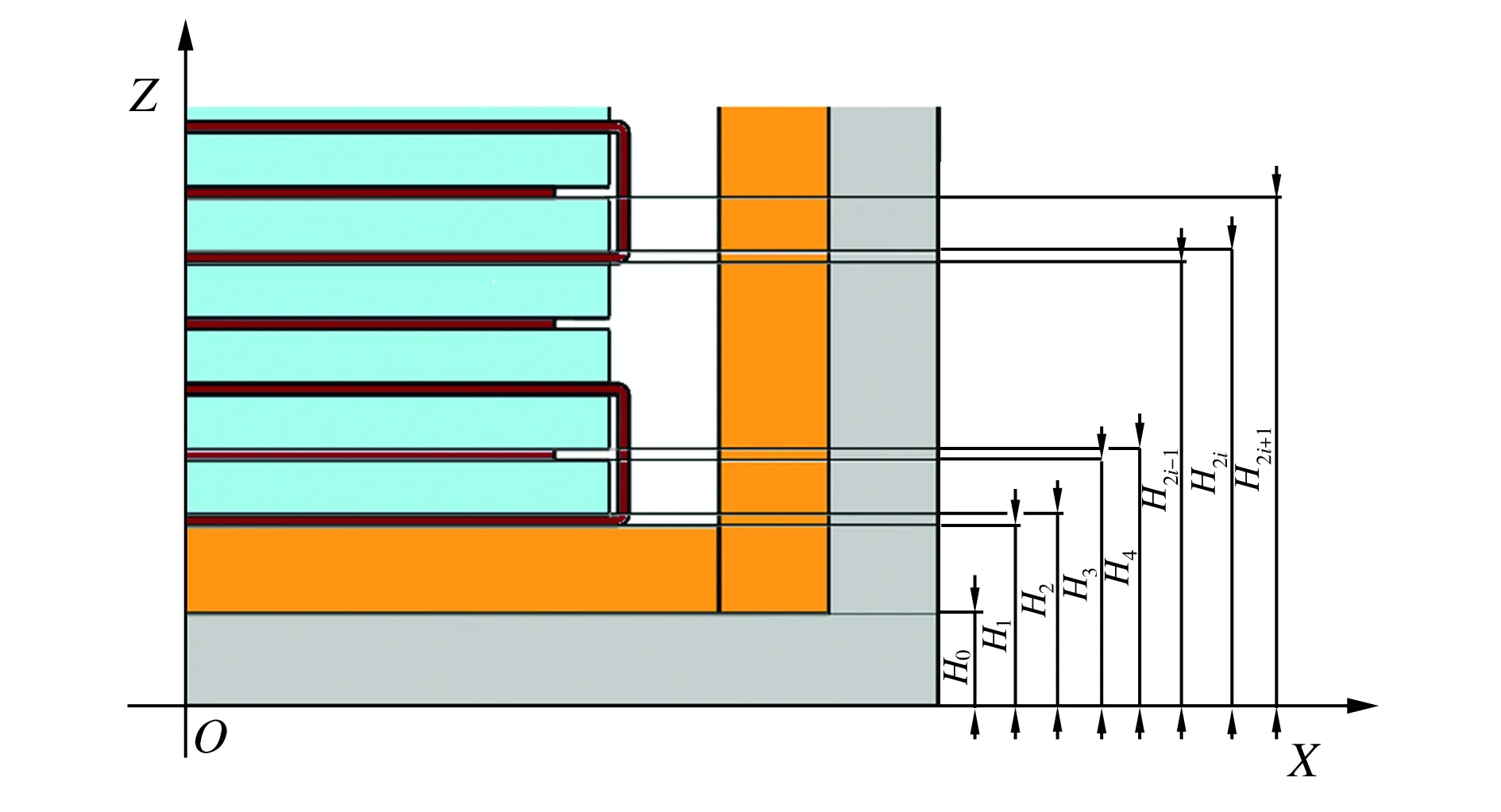
图2 智能骨料的简化模型

(a)串联 (b)并联
图3智能骨料内压电陶瓷的串、并联模型
Fig.3SeriesandparallelmodelsofPZTsinsmartaggregate
为简化计算,对智能骨料模型还作如下假设:
(1)智能骨料仅存在单一轴向振动,且其振动方向与电极的极化方向相同,其它方向上的振动均可忽略[8-9]。
(2)压电层、电极层、金属屏蔽层和水泥保护层均视为理想的弹性介质,并且除压电层外,其它层统称为弹性层。
(3)轴向应力分布是均匀的。
(4)骨料内部的压电陶瓷片视为理想的介电材料,不存在自由移动的电荷,且压电片上、下电极面形成的电场为均匀电场,没有其它方向的分量。
根据以上假设可以得到智能骨料的应力应变及压电方程:
(1)

对于压电层还有如下关系成立:
(2)

由于同一表面的应变相等,故可以得到:
εp=εc=∂W/∂Z
(3)
对智能骨料激发器或传感器施加稳定电压激励V(t)或位移载荷q(t)时,其输出也是稳定的,在本研究中施加的外部载荷表示为
(4)
联立式(1)~式(4)可以得到:
ω2W=0
(5)
其中,对于压电层和弹性层,k分别表示为
(6)
式中:ρ为材料密度。
对式(5)求解可以得出每个面上的位移W和力的幅值N为
(7)

进一步可以得到电势和电位移的表达式为
(8)
1.3 边界条件
对于智能骨料激发器和传感器,其力学边界条件分别为
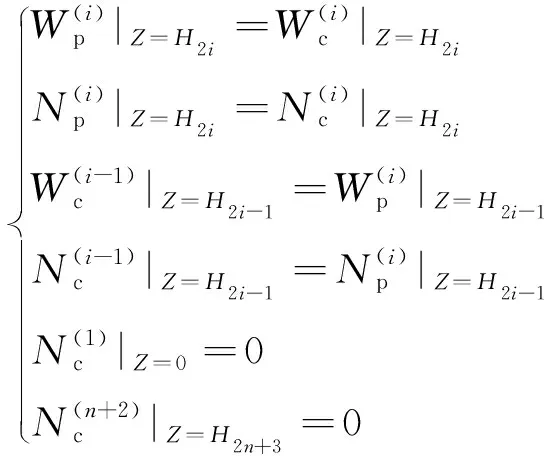
(9)
(10)
压电陶瓷片并联和串联时的电学边界条件分别为

(11)

(12)
当有n个压电陶瓷片叠加时,根据式(9)~式(12)共得到6n+2个方程,而这些方程一共有6n+2个变量,因此由上述边界条件就可以求出这6n+2个未知数。
进一步可得到智能骨料的等效电阻抗Ze为
(13)

(14)
由上式可知,智能骨料的等效电阻抗Ze是关于频率ω的函数,在某些频率下,Ze会达到最小值或最大值,此频率即为谐振频率或反谐振频率,分别表示为fr和fa。
智能骨料的机电耦合系数则可表示为
(15)
对于智能骨料传感器,往往需要其具有较大的输出电压或功率。若压电陶瓷的阻抗为R,则其输出电压为
U(t)=RI(t)
(16)
智能骨料传感器的平均输出功率为
(17)
2 智能骨料特性的数值仿真分析
为了分析和预测智能骨料整体动态特性,本文基于上述理论模型采用MATLAB数值仿真的方法研究骨料结构参数包括压电陶瓷连接方式、压电陶瓷片数、单片压电陶瓷厚度与水泥保护层厚度对智能骨料的谐振频率、机电耦合系数、智能骨料激发器输出位移以及智能骨料传感器输出功率的影响。
在数值仿真过程中,智能骨料的材料参数取值见表1。所用压电陶瓷的类型为PZT-5H,保护层为普通硅酸盐水泥。

表1 智能骨料的材料参数
2.1 智能骨料结构参数对谐振频率的影响
图4为压电陶瓷分别串联和并联叠加时智能骨料的一阶谐振频率随压电陶瓷片数及水泥保护层厚度的变化曲线。由图4可知,随着压电陶瓷片数的增加,其串联和并联叠时的谐振频率及反谐振频率均出现不同程度的下降,但下降趋势会逐渐减缓;随着保护层厚度的增加,串联和并联叠时的谐振频率和反谐振频率均不断降低,同时降低幅度也逐渐减小;相同条件下的反谐振频率均大于谐振频率。另外,对比两种不同的电学连接方式,压电陶瓷片数及水泥保护层厚度相同条件下,串联时骨料的谐振频率与反谐振频率之间的差值大于并联时的对应差值,且串联时的谐振频率小于并联时的谐振频率,而串联时的反谐振频率大于并联时的反谐振频率。这是由于电能与机械能之间的能量转换率大小因智能骨料内部压电陶瓷的电学连接方式的不同而发生变化,由此也可以推知,在其它条件相同时,PZT串联时智能骨料的机电耦合系数要比PZT并联时的机电耦合系数值大。

(a)压电陶瓷串联叠加

(b)压电陶瓷并联叠加
图4智能骨料一阶谐振频率随压电陶瓷片数及保护层厚度的变化
Fig.4Variationofthefirst-orderresonantfrequencywithPZTsnumberandprotectivelayerthicknessofsmartaggregate
图5为压电陶瓷分别串联和并联叠加时智能骨料的一阶谐振频率随压电陶瓷片数及单片压电陶瓷厚度的变化曲线。由图5可见,当压电层厚度增加时,两种连接方式下智能骨料谐振频率与反谐振频率均呈近似线性降低,下降趋势较平缓;串联时骨料的谐振频率与反谐振频率之间的差值同样大于并联时的对应差值,与图4中的结果相一致。

(a)压电陶瓷串联叠加

(b)压电陶瓷并联叠加
图5智能骨料一阶谐振频率随压电陶瓷片数及单片压电陶瓷厚度的变化
Fig.5Variationofthefirst-orderresonantfrequencywithPZTsnumberandPZTlayerthicknessofsmartaggregate
2.2 智能骨料结构参数对机电耦合系数的影响
图6为智能骨料的机电耦合系数随压电陶瓷叠加片数及保护层厚度的变化曲线。由图6可知,压电陶瓷串联叠加方式下智能骨料的机电耦合系数随保护层厚度的增加而近似线性增大;而并联叠加方式下智能骨料的机电耦合系数随厚度增大呈现先增加后减小或基本持平的趋势,且在保护层厚度达到120 mm时,机电耦合系数达到最大值,这是由于保护结构与压电材料组成的机电耦合系统发生了谐振而引起的。对比两种连接方式,串联时智能骨料的机电耦合系数要大于并联时的对应值。这与图4的分析结果相吻合。

(a)压电陶瓷串联叠加

(b)压电陶瓷并联叠加
图6智能骨料机电耦合系数随压电陶瓷片数及保护层厚度的变化
Fig.6VariationofelectromechanicalcouplingcoefficientwithPZTsnumberandprotectivelayerthicknessofsmartaggregate
图7为智能骨料的机电耦合系数随压电陶瓷叠加片数及单片压电陶瓷厚度的变化曲线。由图7可以看出,无论是串联还是并联,增加压电层的厚度均可以使智能骨料的机电耦合系数增大,同样串联比并联时的机电耦合系数略大。由于材料的内摩擦产生机械损耗,使材料发热而消耗能量,并使材料的性能下降,进而影响智能骨料机电耦合系数的大小。智能骨料用于激发器时,一般要求其机电耦合系数大,以提高发射效率;反之,智能骨料用于传感器时,希望能增加带宽,因而需要其机电耦合系数较小,所以应当根据不同的需求选择合适的智能骨料。

(a)压电陶瓷串联叠加

(b)压电陶瓷并联叠加
图7智能骨料机电耦合系数随压电陶瓷片数及单片压电陶瓷厚度的变化
Fig.7VariationofelectromechanicalcouplingcoefficientwithPZTsnumberandPZTlayerthicknessofsmartaggregate
2.3 智能骨料结构参数对输出位移的影响
图8为压电陶瓷叠加片数及连接方式不同时智能骨料激发器的输出位移随加载电压频率的变化曲线。从图8中可以发现,随着加载电压频率的增加,智能骨料激发器的输出位移呈现近似线性的下降趋势;随着压电陶瓷片数的增加,智能骨料激发器的输出位移也在增加,同时压电陶瓷串联时的输出位移大于并联时的输出位移。

图8智能骨料激发器的输出位移随加载电压频率的变化
Fig.8VariationofSAexciter’soutputdisplacementwithvoltagefrequency
2.4 智能骨料结构参数对输出功率的影响
图9为压电陶瓷叠加片数及连接方式不同时智能骨料传感器的输出功率随载荷频率的变化曲线。由图9可知,随着载荷频率的增加,智能骨料传感器的输出功率呈现近似线性的上升趋势,且变化趋势较缓;随着压电陶瓷片数的增加,智能骨料传感器的输出功率也在增加;压电陶瓷串联时的输出功率大于并联时的输出功率。

图9 智能骨料传感器的输出功率随载荷频率的变化
Fig.9VariationofSAsensor’soutputpowerwithloadfrequency
3 结论
(1)智能骨料的谐振频率及反谐振频率随着压电层和保护层的厚度增加呈现出下降的趋势,内部压电陶瓷串联叠加时智能骨料的谐振频率与反谐振频率之间的差值大于并联叠加时二者的差值。
(2)压电陶瓷片串联时智能骨料的机电耦合系数大于并联时的对应值。随着保护层厚度的增加,智能骨料的机电耦合系数总体呈增大趋势,但压电陶瓷并联叠加时,在保护层厚度为120 mm时,机电耦合系数达到最大值。增加单片压电陶瓷厚度可以使智能骨料的机电耦合系数近似线性增加。
(3)智能骨料激发器的输出位移随着加载电压频率的增加而近似线性下降,智能骨料传感器的输出功率随着载荷频率的增加而近似线性上升。压电陶瓷片数对激发器输出位移和传感器输出功率影响较大,且为正相关关系。压电陶瓷串联叠加时的激发器输出位移和传感器输出功率均大于压电陶瓷并联时的对应值。
