基于等级密钥管理的云外包数据安全共享技术*
2018-10-08韩金仓
孙 力, 韩金仓
(兰州财经大学 a. 陇桥学院, b. 信息工程学院, 兰州 730101)
云存储服务随着云计算的快速发展已被越来越多的用户应用,由于在此存储形式下的数据管理者即云服务提供商并不是完全可信的[1],因此要建立相应的机制以确保外包数据的隐私.数据拥有者的云外包数据一般情况下会被多人协作共享且共享权限存在细粒度需求[2],所以云外包数据的安全共享问题也至关重要.通常情况下外包数据的共享可以看做是等级访问控制问题,故本文研究设计了一种基于线性几何等级密钥管理的云外包数据共享技术.
1 等级密钥管理
运用一个偏序集(V,≤)表示等级访问控制中的等级框架,其中V={V1,V2,…,Vn}为用户群组集合,Vi为一个单独用户或多个拥有同等访问权限的用户组成的访问群组,通常状况下称作类.二元关系“≤”为集合V中元素的等级关系,如Vi≤Vj表示类Vj中的用户可以访问类Vi对应的数据资源,即类Vj访问等级比类Vi高.
任何一个(V,≤)均可表示成一个有向图G=(V,E)[3],若Vi,Vj∈V同时Vi≤Vj,则在G中拥有一个从Vj至Vi的有向边.为便于表示,定义两个集合:Anc(Vi,G)及Des(Vi,G),若G中有一条从Vi至Vj的路径,则Vi∈Anc(Vj,G)且Vj∈Des(Vi,G),其代表等级结构中一个访问群组对应的访问权限分别高于及低于其他访问群组集合,故称其分别是Vi的高等及低等级类集.
设Γ表示一个等级访问系统对应的访问图集合,一个等级密钥管理方案包含的两个算法如下:
1) 系统建立算法Gen(lκ,G)[4].其性质是概率性的,输入是安全参数κ及一个等级结构对应的访问图G=(V,E)∈Γ,输出是系统公开参数pub以及每一个类Vi∈V对应的(pi,ki),其中,pi及ki分别为类Vi相应的私有信息以及对称加密密钥.
2) 密钥派生算法Der(pub,Vi,Vj,pi,ki)[5].其性质是确定性的,输入是系统公开参数pub、两个类Vi和Vj以及类Vi对应的(pi,ki),如果输出Vj≤Vi,则输出类Vj对应的对称加密密钥.
2 线性几何等级密钥管理方案
运用线性几何的等级密钥管理方案框架如图1所示.
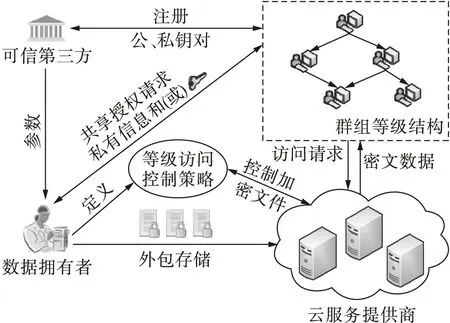
图1 基于等级密钥管理的云外包数据安全共享框架
Fig.1Cloudoutsourcedshareddatasecuritysharingframeworkbasedonhierarchicalkeymanagement
根据图1可知,该方案包括可信第三方、数据拥有者、用户以及云服务提供商.运用等级密钥管理处理云外包数据的安全共享问题时,数据拥有者为该方案中的授权中心角色,加密共享数据同时把加密后的密文传输至云服务提供商的服务器上.另外数据拥有者定义共享群组的等级结构,同时完成用户对外包数据的共享请求.所有用户均能够向云服务提供商提出访问请求,唯有取得私有信息以及对称加密密钥的用户才可解密其共享权限相对应的密文.
伪随机函数F[6]定义为:K×D→RG.其中,K为F的密钥集合,D及RG表示F的域及区间.对k∈K,Fk(x)=F(k,x)代表F的一个实例,设Rand={g|g∶D→RG}为从D至RG上全部的函数集合,hF为一个多项式时间敌手.对于Rand或F中的函数g∶D→RG,敌手hF能够访问预言机.
设定访问群组Vi,Vj∈V,则Vi至Vj的间接密钥为
(1)
式中:ki,i及kj,j分别为访问群组Vi及Vj对应的对称加密密钥;wi,1及wi,2分别为经过伪随机函数F作用于访问群组Vi的私有信息.
方案构建规则如下:
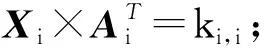
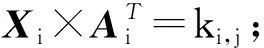

2.1 Gen(lκ,G)算法的系统构建
Gen(lκ,G)算法的构建步骤如下:
1) 对类Vi随机择取非零向量Yi=(yi,1,yi,2)及Zi=(zi,1,zi,2),当做其私有信息.
2) 把全部私有向量Yi经过伪随机函数F映射至一个新的向量Wi,具体过程为:
① 在有限域内随机择取一个公开参数r,随之运算wi,1=Fyi,1(r)及wi,2=Fyi,2(r),i=1,2,…,n;
② 若wi,2=0,则重新选取参数r,然后返回至步骤①重新操作.
把Zi转换成一个n维向量Xi,当i=1,2时,令xi,1=zi,1、xi,2=zi,2、xi,3=xi,4、…、xi,n=0;当i=3,4,…,n时,令xi,1=zi,1、xi,2=zi,2,对于j≠1,均有xi,j=0,则向量X可表示为
(2)
3) 检测X1,X2,…,Xn是否线性独立,若线性无关,执行步骤4);否则返回至步骤1).
4) 针对每个类择取一个对称加密密钥并运算公开矩阵A,其计算步骤如下:
① 对G中的每个类Vi,在有限域内随机择取其对称加密密钥ki,i,运用式(1)计算中间密钥ki,j;
② 依照式(1)得到一个关于公开矩阵A的线性方程组,并设定Kj=(kj,1,kj,2,…,kj,n)及K=[K1,K2,…,Kn]T,则X×A=K;
③ 求解步骤②中的方程组,获得A=X-1×K.
5) 经过安全信道把((Yi,Zi),ki,i)发送至Vi中的每个用户,把F、r及A发送至云服务提供商.
2.2 派生算法Der(pub,Vi,Vj,pi,ki)的构建
若Vi中的用户要得到低等级访问群组Vj对应的共享数据,且Vi∈Anc(Vj,G),则可以通过如下两个步骤获得Vj对应的对称加密密钥:
1) 运用规则2)运算中间密钥ki,j;
2) 经过求解方程kj,j=wi,1ki,i+wi,2ki,j,访问群组Vj中的用户便能够获得其相对应的对称加密密钥.
2.3 动态密钥管理
2.3.1 插入新节点
对Vi,Vj∈V且Vi 2.3.2 删除一个节点 若等级结构中包含n+1个群组,数据拥有者要从中删除一个群组,并设定删除的访问群组是Vl,则务必要对全部访问权限低于Vl的访问群组进行更新以获得其新对称加密密钥,并根据系统构建算法的步骤重新计算获得公开矩阵A.随之完成对相关数据的重新加密,同时传送至云服务提供商. 为了验证算法计算性能,对其开销(存储开销[11]与计算开销[12])进行实验分析.设定有限域内一个元素的大小及系统中访问群组数量分别为L及n,各访问群组对应的低等级类集中元素个数平均值是c. 各访问群组要保存其私有信息Yi及Zi,因为这两个向量都包含两个元素,所以各访问群组中用户的存储开销为4L,数据拥有者务必保存全部访问群组对应的私有信息,故其存储开销等于4nL. 设H为伪随机函数F的一次计算代价,a、m及v分别为有限域上完成加法、乘法以及逆运算的计算代价.要得到访问群组相应的对称加密密钥,各群组成员需在有限域上运算两次乘法以及一次加法;要获得一个访问权限低的群组相应的对称加密密钥,高等级类中的用户要运算2次F,同时还要完成4次乘法以及2次加法[15],故其总计算开销等于2H+(4c+2)m+(2c+1)a. 数据拥有者要运算各群组相应Yi的伪随机函数F值,其计算开销为2nH;随后运算中间密钥ki,j,要完成2cn次乘法以及n次求逆运算;还要运算公开矩阵A,要完成不超过3n2+2n+6次的乘法以及n次求逆运算,故数据拥有者在系统密钥构建历程中总计算开销等于2nH+(3n2+(2c+2)n+6)m+(3n2+(c+2)n+2)a+2nv. 设定L=160,择取数据拥有者及云服务提供商的运行平台是DellT5610的工作站,用户的运转平台为HPXW4600工作站.数据拥有者完成系统密钥构建、密钥派生以及密钥管理的时间开销分别如图2~4所示. 图2 完成系统密钥构建的时间开销Fig.2 Overhead time of completed establishment of system key 根据图2及图3可知,系统密钥构建以及密钥派生时间开销依着访问群组数目n及参数c的逐渐升高而逐步升高.另外实验中各用户得到任何低等级访问群组对应的对称加密密钥的时间是0.001 9 ms.在确定低等级访问群组集合的前提下,当c=5及c=10时用户得到全部低等级访问群组对应的对称加密密钥时间分别是0.050 8 ms及0.068 9 ms.任何一个访问群组中的用户在密钥派生时,首先经过检测中间密钥值是否等于0,然后再运算全部低等级访问群组对应的对称加密密钥的时间开销. 图3 密钥派生的时间开销Fig.3 Overhead time of key derivation 图4 动态密钥管理的时间开销Fig.4 Overhead time of dynamic key management 根据图2及图4对比可知,动态密钥管理的计算时间要稍微高一点,其主要原因是在密钥动态管理时,数据拥有者需要搜索访问图G以获得哪些是需要更新的节点,然后重新择取对称加密密钥及与运算相关的中间密钥. 本文设计了基于线性几何的等级密钥管理云外包数据安全共享方案,详细阐述了系统构建算法、密钥派生算法以及动态密钥管理等3条规则.数据拥有者为各访问群组公开一个向量,每个访问群组的私有向量与其公开向量的内积作为其对称加密密钥.运用间接密钥,高等级访问群组中的用户能够得到低等级访问群组的对称加密密钥.在解决动态共享权限密钥管理过程中,数据拥有者仅需更新系统中的公开矩阵即可.根据实验结果分析可知,该方案是安全且相对非常有效的.3 实验分析
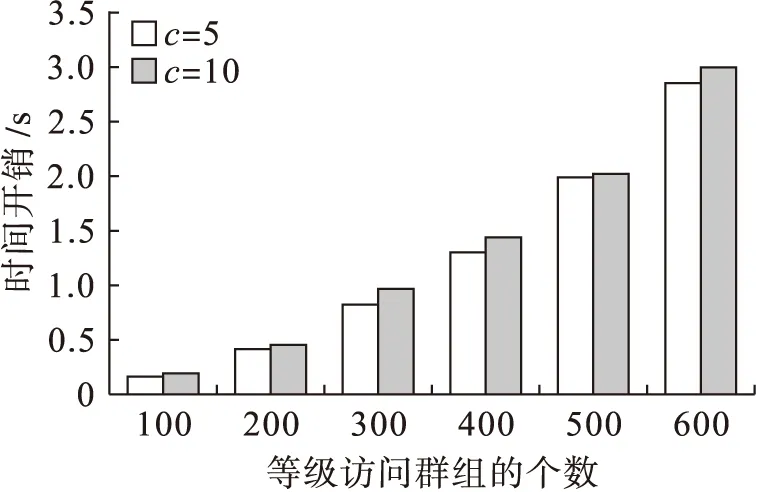
4 结 论
