预处理方法在混合笛卡尔网格中的应用研究

2018-10-08干雨新

空气动力学学报 2018年4期

干雨新, 赵宁

(南京航空航天大学航空宇航学院, 江苏南京 210016)

0 引言

近年来，随着计算机技术的迅猛发展，数值模拟方法成为了人们科学研究的重要热点。在流体力学领域，计算流体力学(Computational Fluid Dynamics，CFD)也成为了一门新兴且热门的学科。使用CFD方法进行数值模拟，对计算区域的空间离散即网格生成技术是关键。网格质量的好与坏，对计算结果的影响非常大，尤其是对于复杂外形的网格生成，即便对于一名熟练掌握网格生成技术的学者也是一件耗时耗力的事情。笛卡尔网格[1]应运而生，其相比于传统的贴体网格，具有网格结构简单、便于自动化生成、人工干预少、实现自适应容易等优点，尤其是善于处理多物体和复杂几何外形的网格生成问题。对于N-S方程的求解，考虑流体的黏性作用，需要生成极薄的附面层网格。传统的浸入边界的各向同性笛卡尔网格方法，考虑到附面层网格的厚度，需要在附面层里布置大量的小尺度网格单元，这大大增加了网格数量(尤其对于三维问题布置的大长宽比六面体单元而言)。所以，在计算物体周围生成贴体的附面层结构网格，而在其他计算区域用笛卡尔网格填充的混合笛卡尔网格[2]成为了一种有效的解决问题的手段。含有重叠区域的混合网格的难点在于混合网格的生成以及重叠区域的处理，Wang[3]使用重叠自适应笛卡尔网格模拟了固定和运动边界的流动问题；张来平等人[4]对于结构非结构和笛卡尔的混合动网格技术进行了深入的研究；肖天航等[5]则应用变形重叠网格对非定常流动进行了数值模拟。

通常认为，马赫数低于0.3的流动问题，属于不可压流动问题。对于不可压N-S方程的求解，直接采用可压缩N-S方程求解的基于密度的方法由于速度过低，会导致方程的几个特征值的量级差距过大，从而导致方程的刚性过大，使得求解收敛缓慢且结果错误。而使用基于压力的不可压方法比如SIMPLE算法等则无法和可压缩求解方法得到有效的统一。所以，对基于密度的可压缩N-S方程求解算法进行预处理，使方程的特征值处在同一个量级，从而使可压缩N-S方程求解器能求解低速不可压流场具备很大的意义。Turkel[6]经过研究指出，对于低速流动，预处理方法可以通过对时间导数的预处理达到加速计算收敛的效果，并且改变中心格式或迎风格式的耗散来提高计算的精度。Weiss和Smith[7]则提出了基于N-S方程守恒变量的预处理矩阵，从而将基于密度的方法应用到了低速黏性计算中。国内也有很多学者对低速预处理方法进行了研究[8-10]。本文使用基于混合笛卡尔网格的预处理方法，对NACA0012翼型在极低马赫数下的定常绕流和动态失速进行了数值模拟，验证了所发展的低速预处理方法的正确性。耦合预处理技术的混合笛卡尔网格方法具备高效求解定常/非定常流动的能力。

1 混合笛卡尔网格方法

1.1 混合笛卡尔网格生成

生成计算物体的贴体结构网格，选定计算区域，并以贴体结构网格的外边界为几何边界，生成背景笛卡尔网格，两套网格相互重叠，并在附近使用了加密的笛卡尔网格来尽量使得两套网格系统之间的尺度过渡平缓。以NACA0012翼型为例，生成的混合笛卡尔网格如图1所示。

图1 NACA0012翼型的混合笛卡尔网格局部放大Fig.1 Local enlarged hybrid Cartesian grid of NACA0012 airfoil

在生成混合笛卡尔网格的过程中，本文首先在计算区域全场生成背景笛卡尔网格，然后根据贴体结构网格的最外层(称之为“交界面”)来进行笛卡尔网格单元的分类，判断其为“洞外单元”、“洞边界单元”或“洞内单元”，完成“挖洞”操作[11]。为了提高搜索效率，可以将贴体结构网格存储为二叉树的数据结构，使用了基于ADT技术[12]的单元搜寻方法，来快速找出洞内单元。

1.2 贡献单元查找

对于笛卡尔网格和贴体结构网格的重叠区域，在进行交界面上通量计算过程中，左单元在各自的网格系统里很容易确定，但右单元需要到另外一套网格系统里寻找，即寻找所谓的“贡献单元”。本文采用Munikrishna和Liou给出的“贡献单元”选取方法[13]。“贡献单元”的寻找过程中同样使用了ADT技术来加速搜索过程。

1.3 非定常运动问题的新现单元处理

在计算物面边界运动的非定常问题中，由于贴体网格随着物面一起运动，所以原先被覆盖的标记为洞内单元的笛卡尔网格会显现出来，成为新现的网格单元，参与流体计算，所以对于新现单元的处理显得尤为重要。

本文对于新现网格单元的具体处理方法可以参考文献[14]，如图2所示，贴体结构网格从图中黑色位置运动到红色位置，则网格单元I为新现网格单元。对于新现网格单元I上流场信息的确定，主要做法是首先寻找新现网格单元I周围的原洞边界单元(即图2中的网格单元1，2，3)，将这些单元作为插值的模板单元使用权系数为逆距离的插值公式计算新现网格单元上的流场信息，插值公式如下：

图2 非定常计算新现单元的处理方法Fig.2 Method of new cell on unsteady calculation

2 控制方程与预处理方法

2.1 控制方程

积分形式的非定常N-S方程如下：

其中，

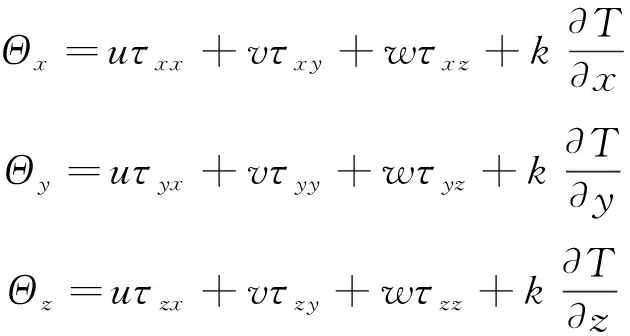
Vr为逆变速度V=V·n相对于运动网格的速度，其表达式为Vr=V-Vt=nxu+nyv+nzw-Vt,其中Vt为网格运动的速度。

2.2 预处理方法

首先将对于守恒变量W的N-S方程转化成关于原始变量Q=(P,u,v,w,T)的形式：

预处理方法则是将雅克比矩阵M替换为预处理矩阵Γ，本文选用Weiss-Smith预处理矩阵，矩阵形式如下：

其中，

Ur=min(c,max(V,KV∞))(9)

其中，V∞为来流速度，常数K取值为1～4，对于黏性流动，参考速度Ur还需要满足：

其中，Δd为网格尺度。

引入预处理矩阵Γ后，N-S方程变为：

则此时对流通量的雅克比矩阵的特征值为：

λ1,2,3=V,λ4,5=V′±c′

V′=V(1-a)

其中，V′和c′为伪速度和伪声速。在低速条件下，参考速度Ur≪c，伪速度V′和伪声速c′都是V的量级，降低了方程的条件数，从而改善了方程的收敛性质。当参考速度Ur=c时，a=0，则伪速度和伪声速等于真实的速度与声速，方程的特征值自动退回到预处理之前的形式，从而起到了关闭预处理的作用。

需要指出，使用预处理技术后，改变了N-S方程的特征系统，原本基于黎曼不变量的远场边界条件将不再适用，需要根据新的特征值来计算新的黎曼不变量。为简化远场边界的处理，本文采用Turkel等提出的边界条件[15]，对于入流远场边界：

ub=u∞,vb=v∞,wb=w∞,Tb=T∞,Pb=Pint(13)

对于出流远场边界：

ub=uint,vb=vint,wb=wint,Tb=Tint,Pb=P∞(14)

其中，下标b为远场边界处的流场信息，下标int为内部单元的流场信息，下标∞为来流的数值。

同时，由于预处理方法改变了方程的特征系统，对流通量的求解也要相应的改变。本文对流通量求解使用HLLC格式[16]，进行预处理后只需将波速计算中的特征值改为低速预处理后的特征值即可。

2.3 非定常流动数值方法

对于非定常流动，通常采用双时间步对N-S方程的时间导数项进行离散，本文采用双时间步的LUSGS[17]预处理方法，物理时间采用二阶向后差分离散，虚拟时间采用一阶差分离散，离散后的方程为：

时间推进采用隐式LUSGS方法，引入低速预处理后求解过程如下：

向前扫：

(MΓ-1ΔF*-λijΔW*)](16)

向后扫：

(MΓ-1ΔF-λijΔW)(17)

3 算例与分析

3.1 NACA0012翼型定常绕流

对NACA0012翼型在马赫数为0.00001、0.0001、0.001、0.01、0.1、0.3、0.5和0.6这八个状态进行了数值计算，迎角α=3.59°，雷诺数Re=1.85×106，使用SSTk-ω湍流模型[18]，计算使用的混合笛卡尔网格如图1所示。

该算例中，研究了不同马赫数下预处理对计算收敛性的影响。从图3可以看出，在马赫数从0.01到0.3的低速范围内，预处理技术起到了非常明显的加速收敛作用。在不使用预处理的情况下，随着马赫数的降低，收敛性能逐渐变差，当马赫数为0.01时，计算基本无法收敛，这是由于在马赫数很低时，系统刚性明显，方程组的耦合性很差，导致收敛性过差。而使用预处理技术后，系统刚性问题得到有效改善，收敛性明显提高，而且收敛的残差下降过程基本和马赫数无关。图4给出了在三种极低马赫数下的加入预处理技术后的残差收敛曲线，同样可以看出残差的下降过程在收敛到“机器零”前和马赫数无关。图3和图4表明，在低速情况下，使用预处理技术可以大大改善方程的刚性问题，使收敛性得到大幅度提高。图5为在马赫数为0.5和0.6的亚、跨声速范围内，预处理对流场计算的影响，此时由于马赫数变高，预处理的影响变小，在高马赫数情况下，方程具有良好的耦合性，预处理的影响也逐渐变小，但依然对计算收敛的加速有一定影响，因为此时流场中有一部分的低速区，比如翼型附面层和驻点附近[19]。该算例表明，本文开发的基于混合笛卡尔网格的预处理方法，将基于密度的可压缩N-S方程求解方法拓展到了从低速(极低马赫数)到常规马赫数的流场，使用预处理方法后可以达到加速收敛和提高计算精度的目的，这和Turkel的结论是一致的。

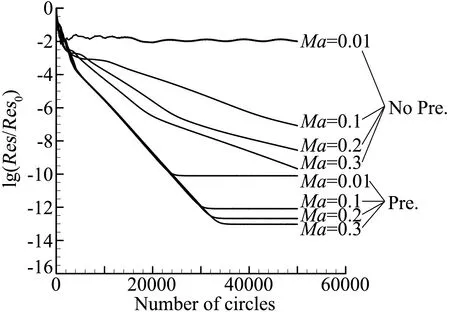
图3 预处理对NACA0012翼型低速计算收敛性的影响Fig.3 Effect of precondition on the convergence of NACA0012 airfoil at low speed

图4 预处理对NACA0012翼型极低马赫数计算收敛性的影响Fig.4 Effect of precondition on the convergence of NACA0012 airfoil at very low Mach number

图5 预处理对NACA0012翼型亚、跨声速计算收敛性的影响Fig.5 Effect of precondition on the convergence of NACA0012 airfoil at subsonic and transonic simulations

3.2 NACA0012翼型的低速俯仰震荡

在翼型的低速俯仰震荡问题中，尤其在迎角超过翼型的失速迎角后，翼型的背风面流动会发生分离从而动态失速，此时翼型背风面的流动情况及其复杂，不少学者对该问题做了数值计算[20]与实验进行研究，选用Lee等[21]做的典型的低速实验状态来验证本文的非定常低速预处理方法。该状态下来流马赫数为Ma=0.0385，雷诺数为Re=1.35×105，使用SSTk-ω两方程湍流模型，迎角变化规律为α(t)=αm+α0sin(ωt)，其中αm=10°，α0=15°，缩减频率为k=ωt/(2V∞)=0.1。网格与前文保持一致，贴体结构网格部分随着翼型一起做俯仰震荡，交界面新现单元的处理在2.3节已经做了阐述。

使用混合笛卡尔网格的非定常预处理方法，对NACA0012翼型在上述状态下进行了6个周期的俯仰震荡计算，图6为非定常计算双时间步中第一个物理时间步下的收敛曲线，从曲线中可以看出预处理技术可以有效改善非定常计算伪时间迭代上的系统刚性，起到加速收敛的效果。

图7给出了翼型俯仰震荡过程中几个迎角下的预处理结果和Lee等的实验[21]观察到的流场的比较，从中可以看出，一开始流动附着在翼型表面，随着迎角的增加，翼型上表面前缘逐渐出现前缘涡(LEV)，然后随着迎角继续增大，前缘涡也逐渐变大并往翼型

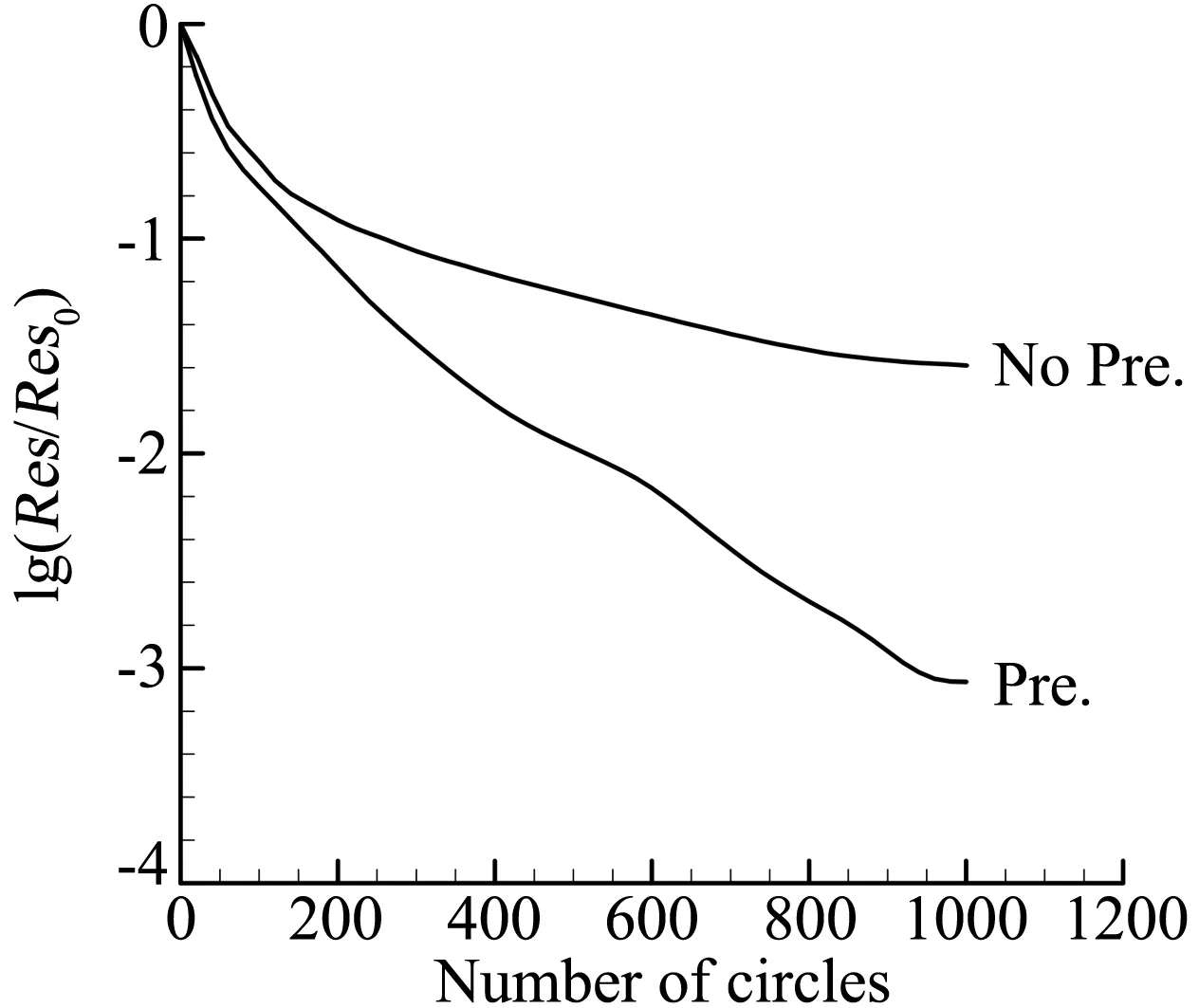
图6 预处理对NACA0012翼型低马赫数非定常计算收敛性的影响Fig.6 Effect of precondition on the convergence of NACA0012 airfoil′s unsteady calculation at low Mach number

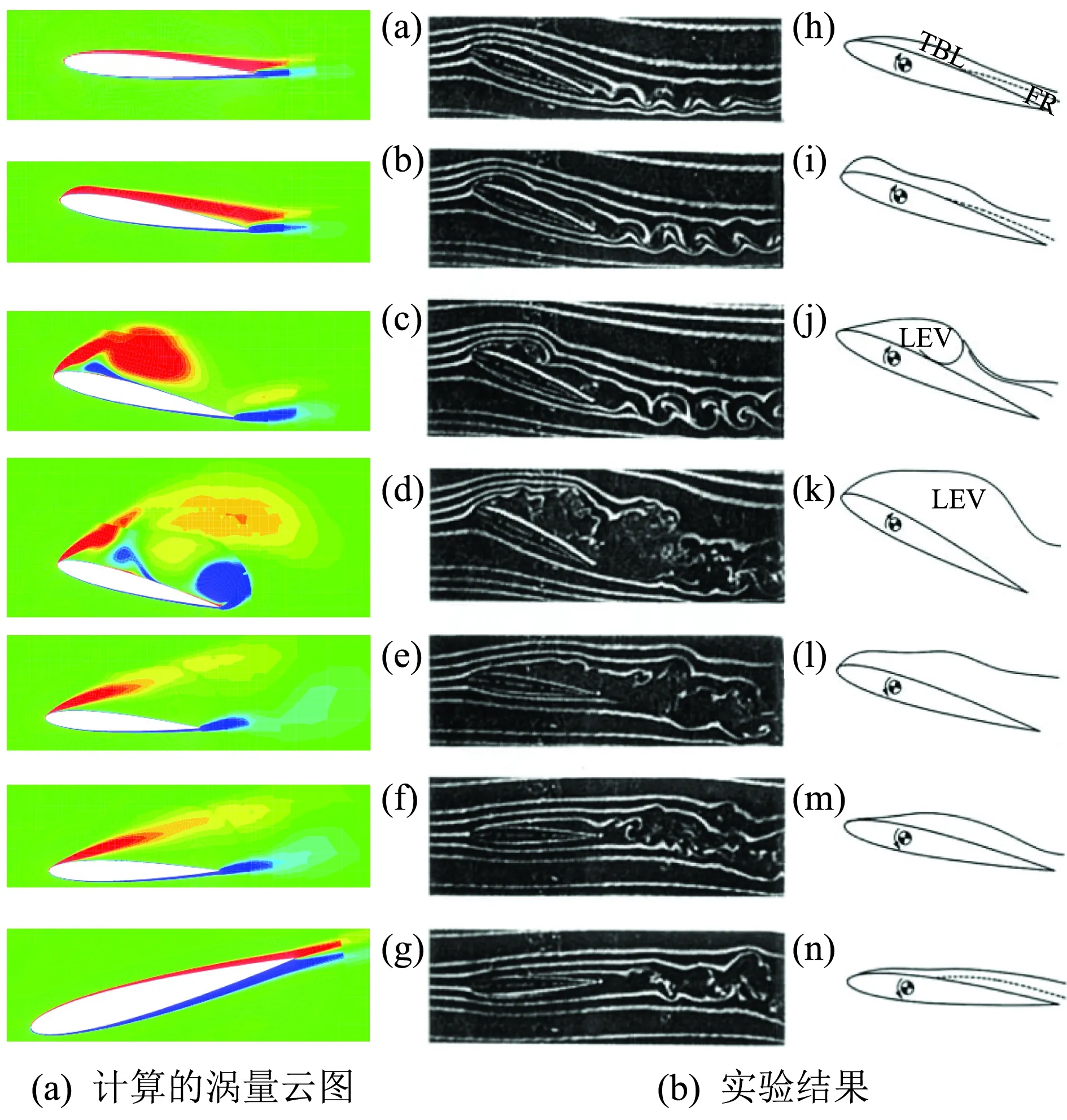
图7 NACA0012翼型低速动态失速过程中不同时刻的流场Fig.7 NACA0012 airfoil dynamic stall at low speed and different time

上表面后缘移动，升力也逐渐增大。随着迎角增加到24.7°，前缘涡破裂，翼型上表面流动完全分离，升力迅速下降。接着迎角逐渐变小，翼型上表面的流动也随着迎角变小而逐渐慢慢附着到翼型表面上，直到最后完全附着。

图8和图9为NACA0012翼型俯仰震荡升力系数和力矩系数的迟滞曲线，从图中可以看出，数值模拟结果和实验结果虽然稍有差别，但较为准确的模拟出了翼型动态失速的规律。在失速前的上仰阶段，翼型气动力和实验结果符合较好，但随着迎角增大，翼型失速后的升力系数和力矩系数均与实验值有所偏差，但和未加预处理的结果相比，和实验值的误差大大降低。不进行预处理的计算结果无论在数值上还是在变化趋势上和实验结果相去甚远，预处理的结果虽然和实验结果稍有偏差，但依然能较为准确的捕捉到动态失速的规律。图8和图9中红色点划线为变形网格方法[22]的计算结果，可以看到，其模拟结果也和实验结果存在偏差，而且从图中可以看出本文用混合笛卡尔网格预处理的模拟结果和实验更为接近。