一种用于获得飞机部件气动载荷的网格向量法
2018-10-08刘晓晨胡赞远闫中午
韩 鹏, 刘晓晨, 胡赞远, 闫中午
(上海飞机设计研究院, 上海 201210)
0 引 言
一架飞机,在整个飞行过程中,无时无刻不承受着载荷。从不同受载情况中找出各个部件的最大受载情况,其载荷的大小及分布情况将作为飞机结构与强度的设计依据。选用合适的飞行载荷规范和可靠的计算方法是获得合理、可靠的载荷的重要条件[1]。
确定一架飞机的飞行载荷,需要解决两方面问题:第一,总载荷计算,即机动模拟。根据规范要求和工程设计经验选定计算的原始数据,将问题抽象为一定的物理模型,并通过数学方法对此物理模型做出描述,求解这些数学问题即可确定飞机的运动参数及总载荷;第二,分布载荷求解。确定了飞机的运动参数及总载荷,为了进行强度计算,还要知道这些力的分布。
目前,国内外大量的相关文献和研究方向主要集中在机动模拟和CFD及理论计算方面。王世安、尹贵鲁等采用CFD方法确定基本气动载荷,并引入工程估算方法得到的偏副翼附加量[2]。国外的Patil、Hodges及国内的杨超、王立波等在机动模拟中考虑了气动载荷与结构变形的耦合作用,即气动弹性效应[3-9]。万志强、严德等在考虑静气弹影响的载荷计算时引入试验气动力修正[10-11]。以上研究都是建立在理论计算和数值模拟的基础上,并且都是以飞机的主要部件载荷(如机翼、尾翼)为研究重点,而关于飞机小部件(如舱门类部件)的载荷计算研究文献则相对较少。吴继飞、王明等利用风洞试验对舱门类载荷的气动特性进行了研究[12-13]。对于舱门类部件的载荷求解,由于其外形不规则且绕流特性复杂,无论是网格生成还是流动模拟都十分困难,所以通常采用风洞试验的手段确定其气动载荷。
在飞机详细设计阶段,要完成大量的风洞测压试验以确定飞机真实载荷。此方法通过在部件外形表面布置测压传感器以获取压力分布,将其积分即可得到各部件的总载荷。常规的测压数据处理方法包括剖面积分法[14-16]和投影法,剖面积分法通常只适用于典型翼面类部件,如机翼、尾翼等;投影法的实质是把飞机部件上的载荷进行投影分解,然后在投影面内获取计算部件气动载荷的基本要素(如作用中心、面积、力臂等),获得这些因素往往需要大量人工测量操作,并且此方法无法考虑飞机部件的真实外形,特别是对形状不规则的小部件,其计算精度不足,效率不高。因此,本文提出采用网格向量法求解飞机部件气动载荷。此方法通过网格化飞机部件气动外形以获取网格点坐标,构造出基础向量,使用空间向量法求解气动载荷的几何要素,进而获得飞机部件在不同情况下的总载荷与分布载荷。
1 物理模型分析
飞机部件气动载荷的计算问题可以简化为一个基本物理模型,即飞机部件上任意分块上所受气动力的计算问题。如图1所示有一任意气动分块,当地压

图1 部件气动载荷物理模型Fig.1 Physical model of aerodynamic loads on airplane
强为P,e为空间任意方向向量,AB为任意轴。此分块的气动载荷问题包括两个方面:1) 此分块所受气动力F及F在任意方向上的分量(因为有不同的分块,求部件总力时,需要分解到不同的方向);2) 此分块气动载荷F对任意轴AB产生的力矩M。
其中,获取力矩M需要先确定力F垂直于轴AB的分解力和作用力臂,如图2所示。

图2 气动力分解及作用力臂Fig.2 Component forces and the arm of force
气动力及力矩的计算公式为:
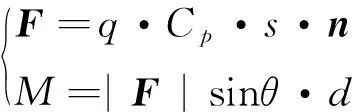
式(1)中,q为速压,可由载荷计算工况确定;Cp为压力系数,通常由风洞试验和CFD计算获得;s为气动分块面积;n为气动分块的单位法向向量;θ为F与轴AB的夹角(如图2所示);d为F到轴AB的距离。其中,速压q和压力系数Cp是气动载荷计算的气动要素,在载荷计算的过程中是输入条件;s、n、θ和d是气动载荷计算的几何要素,可通过飞机部件的几何模型获取,本文采用空间向量法求解这些几何要素。
2 网格向量法
要获取部件的总力和总力矩,需要把部件进行网格化离散,先分别求取各小分块的气动载荷,然后通过叠加求和获得部件的总力和总力矩。
2.1 网格化几何模型
飞机部件的气动外形可用空间中的曲面表示。如图3所示,网格化空间曲面,获取网格点坐标。参考转轴(如铰链轴)可由其上任意两点代表。网格点和参考轴上任意两点组成能够代表几何模型特征的基础点库,用于构造基础向量。

图3 曲面网格化Fig.3 Mesh grid of surface
网格化时,需要注意以下三点:1) 按气流流动特性,尽量顺气流方向划分网格;2) 为了保证计算效率,网格密度不宜太高,但要高于测压点密度,以保证数据完整性;3) 划分网格时,建议全部采用四边形网格,以保证网格格式一致,方便程序化处理。
2.2 单个网格的气动载荷
通过网格化,空间曲面被划分为多个气动网格分块,第i个网格如图4所示:

图4 网格分块及构造向量Fig.4 A grid and vectors


如式(3)所示,g1和g3构成向量v1,g2和g4构成向量v2:
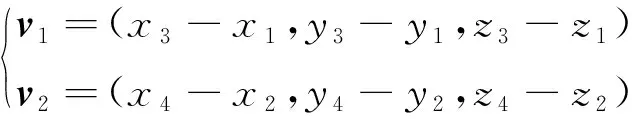

气动网格可以简化等效为由向量v1和v2构成的平面(如图4所示),则网格面积为:
si=0.5v1×v2(4)
网格的单位法向向量为:

网格单位法向向量与参考转轴之间的夹角为:

网格气动力到参考转轴之间的距离,即力臂为:

由式(4)-(7),可以得到网格气动载荷的四个几何要素,把si、ni、θi和di带入式(8),即可得到网格气动载荷:


2.3 部件总载荷及限制载荷
获得了网格气动载荷,通过叠加求和即可得到部件总载荷。由于网格气动载荷的方向不尽相同(法向向量不同),叠加载荷时,需要先进行分解,空间中的力可以分解到正交的三个方向,如e1、e2和e3三个单位方向向量,则总载荷为:

其中,Fe表示e方向的总气动力,e代表e1、e2和e3。对总载荷进行无量纲化,得到力系数与力矩系数为:



式中,上标j表示第j种计算工况。此种情况下的分布载荷为:

对于载荷专业,常常需要从几万或几十万种计算工况中挑选出最大载荷作为限制载荷提供强度专业使用。通常,求解策略有两种:1)从压力系数数据库到分布载荷,再到总载荷,然后从中挑选出最大载荷及对应情况分布载荷;2)从压力系数数据库到总载荷系数数据库,再到总载荷,从中挑选出最大载荷,再由压力系数数据库给出对应情况的分布载荷。在进行批量计算时,推荐使用第二种策略,因为第二种策略省去了大量中间计算环节,能够显著提高计算效率。
3 算例分析
3.1 实例介绍
在飞机的所有部件中,选取具有典型性的起落架内舱门作为研究对象。如图5所示,起落架内舱门外形不规则,不是典型的翼面类部件,经典的剖面积分法无法实施,通过投影获取气动载荷的几何要素也较难操作,因此,本文采用网格向量法完成风洞试验测压数据库的处理,进而用于求解内舱门气动载荷。

图5 飞机模型Fig.5 airplane model
风洞试验给出了舱门打开时,不同位置、不同迎角、侧滑角时的压力分布,模拟了起落架舱门在空中打开过程中的气动受载情况。试验的迎角范围为-6°~18°,侧滑角范围-18°~18°。
根据规范要求完成飞机的各种机动模拟,根据经验选取出需要分析的飞行状态作为起落架舱门的计算工况,其中包括纵向情况1万多种,横向情况2万多种,载荷专业需要对以上所有情况进行计算求解,因为工况数量较大,为提高计算效率,本文采用2.3节提出的第二种求解策略。
3.2 测压试验数据处理
因为起落架内舱门的厚度相对于其他两个方向的长度较小,气动外形模型可用空间曲面表示。如图6所示,网格化离散气动外形,得到98个网格,获取网格点坐标信息。需要注意的是,网格多为四边形网格,而边界上较难划分成四边形的,有呈现为三边形的,此种情况,可另外选取较长边界的中点坐标信息,以满足每个网格由四个网格点表示。

图6 气动网格Fig.6 Aerodynamic mesh
得到了能够代表舱门气动外形的网格点坐标信息,采用网格向量法完成风洞试验压力分布数据库的数据处理,得到力与力矩系数的数据库,其中,力与力矩系数的公式及定义详见本文2.3节式(10)。由于数据较多,这里只展示内舱门打开到图5所示位置的力系数与力矩系数的侧向结果,如图7所示,给出了力系数CF1、CF2与力矩系数CM在迎角0°、4°和8°情况下随侧滑角变化的曲线。
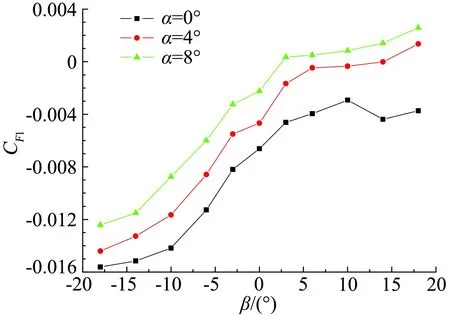


图7 力与力矩系数Fig.7 Force coefficient and moment coefficient
在起落架左侧内舱门的局部坐标系中(如图6中所示),x向(前后方向)载荷分量较小,可以忽略,另外两个方向的力分别为F1和F2。规定F1的正方向为y轴正向,F2的正方向为z轴负向,M的正方向为x轴负向,F1、F2和M为正时,表示使舱门关闭。从图7可以看出,随着侧滑角负向(飞机左侧来流)增大,左侧舱门打开载荷增大,随着迎角增大,舱门关闭载荷增大,其与真实流动规律一致。
基于力与力矩系数数据库,参考式(11)通过插值即可快速高效完成起落架内舱门气动载荷的批量计算。
3.3 结果验证及两种策略计算效率对比
为了验证计算方法的有效性,将某工况的分布载荷加载到有限元模型上,得到累积总载荷并与本文方法的求解结果进行比较,详见表1。

表1 不同方法的总载荷结果Table 1 Total loads of different methods
由表1可以看出:此工况下,两种网格向量法求解策略的计算结果与有限元模型获得的累积总载荷基本一致,说明本文提出的网格向量法正确有效;两种策略获得的总力矩与有限元模型上的累积总力矩稍有偏差,主要是由于网格载荷作用点与有限元结点位置稍有偏差;策略一是对压力系数进行插值,使用式(9)完成总载荷求解,策略二是对总载荷系数进行插值,使用式(12)完成总载荷求解,两种策略的结果差异在于插值带来的误差,只要数据库密度合适,这种误差相当小,正如表中结果显示,两种求解策略结果高度一致,说明风洞试验的状态密度选取合适。特别说明,为了避免个别样本的独一性,另对多个计算工况进行了求解,得到的结果均与表1类似,这里不再给出。
通过以上分析,说明两种计算策略的精度都能够满足工程要求,而对于批量载荷求解,还需要方法具有一定的计算效率,因此对两种计算策略的效率做以下对比, 详见表2。

表2 两种方法的计算时间Table 2 Computing time of two methods
两种计算策略均采用Matlab软件编程计算实现,表2给出了两种计算策略求解不同工况数量时的计算耗时。由表2可以看出:策略一的计算耗时随计算工况数量的增加单调线性增加,这是因为在此计算策略下,每一种工况都要单独完整运算,计算时间会随着工况数增加而增加;策略二的计算耗时基本不随计算工况数量的变化而变化,因为此种计算策略的计算耗时主要在于力与力矩系数数据库的计算处理上,而总载荷的获得只需要对总载荷系数数据库进行线性插值即可完成,所以计算耗时基本不随计算工况数增加而变化;工况数量较大时,策略二的计算效率显著优于策略一,这是因为策略二通过对总载荷系数数据库插值获取批量总载荷替代了策略一中大量的中间计算环节,从而显著提高了计算效率。
4 结 论
通过以上理论分析、方法介绍和算例分析,得到以下主要结论:
1) 网格向量法原理正确、操作简单、结果有效。适用于飞机的所有部件,特别对飞机小部件气动载荷计算具有显著的优越性。
2) 批量载荷求解时,先完成对压力分布数据库的处理,得到部件总载荷系数数据库,进而通过插值快速高效地完成批量载荷计算。这种计算策略,能够显著提高计算效率。
3) 为了获得足够精度的计算结果和较高的计算效率,划分网格时,需要特别注意:尽量顺气流方向划分网格;网格全部采用四边形格式;网格密度略高于测压点密度。
