扑翼飞行器具有弹性阻尼扑动机构的能耗对比分析与研究

张威，刘光泽，张博利

1. 中国民航大学 航空工程学院，天津 300300 2. 中国民航航空地面特种设备研究基地，天津 300300 3. 中国民航大学 基础实验中心，天津 300300

自然界中的鸟类和昆虫主要是利用自身翅膀的上下拍动来实现飞行。同时，昆虫可以凭借翅膀的快速拍动、弯曲和扭转等特性，充分利用非定常气动特性来获得高升力和高升阻比从而完成前飞、悬停、急转等飞行动作[1-2]。学习飞行生物的这些优点，借鉴并利用其机体结构和飞行机理，研制高机动性、低能耗的扑翼飞行器,具有广阔的应用前景[3]。在军用领域，微小扑翼飞行器(Flapping Wing Micro Air Vehicle, FWMAV)可以在特殊环境下进行伪装侦查、追踪目标、近距离电子干扰等；在民用领域，微小扑翼飞行器可以进行狭小空间救援、森林野生动物检测、空中视频拍摄等[4]。

正是由于扑翼飞行器具有如此突出的优点，具有实用价值的扑翼飞行器的探索和研制正在成为多个学科的研究热点。在扑翼飞行器的气动性能实现方面，前人研究了翅翼的柔性变形对扑翼气动特性的影响[5-7]，以及昆虫翅翼褶皱结构对扑翼气动性能的影响[8-10]。在满足空气动力学的条件下，对太阳能电池板作为扑翼飞行器翅翼能量供应的可行性进行了分析[11-13]。扑翼飞行器样机实现方面：美国哈佛大学研究的仿昆虫扑翼飞行器是世界上第1款昆虫大小的扑翼飞行器，它的重量只有60 mg，翼展3 cm。由于飞行器结构的微观性，各结构部件都是采用精密加工，利用压电驱动材料的振动来带动两侧材料的拍动[14-15]；德国Festo公司研制的仿海鸥扑翼飞行器，总重485 g，翼展1.96 m，与其他扑翼飞行器不同的是该飞行器可实现翼面的折叠弯曲，并可用尾巴的扭转实现身体偏航和俯仰[16]。此外，美国AeroVironment公司、加州理工学院、多伦多大学、佐治亚技术研究所、佛罗里达大学、Vanderbilt大学等单位也在DARPA(Defense Advanced Research Program Agency)等的支持下研制了不同结构的微小尺度扑翼飞行器，其翼展一般会在15 cm左右，多采用电池提供能源，飞行时间约在几分钟到十几分钟不等[17-19]。加州大学伯克利分校研制的“机器苍蝇”扑翼飞行器总重约为43 mg，直径为5～10 mm，采用太阳能电池和压电驱动[20]。在中国，西北工业大学研制的扑翼飞行器采用聚合物锂电池和微型电机驱动，可使扑翼在15～20 Hz左右的频率范围内拍动。南京航空航天大学研制了一款多段柔性变体扑翼飞行器，其骨架主要由树脂和碳纤维等材料制成，该飞行器不仅可以完成平飞、爬升和偏航等动作，而且还可以实现“扑动-折弯-扭转”的多维协同运动[21-23]。上海交通大学研制的微小型扑翼飞行器采用压电陶瓷晶片驱动，传动系统将驱动器的振动传递到机翼，驱动两侧翅翼上下拍动[24]，其单翅长15 mm，翅膜厚1.5 μm，由于尺寸较小，机体各部分零件主要采用微尺度机械加工方法[25]。

除此之外，在扑翼传动机构的优化方面也有工作展开[26-29]。Khatait[30],Tantanawat[31],Wu[32]论证了可在扑翼机构上增加柔性装置来减小直流电机的最大转矩。Madangopal等[33]利用非线性优化工具，设计了一个与负载相连的弹簧摆动机构，以减少电机转矩的变化。“Microbat”扑翼飞行器的扑翼机构采用参数完全一样的两套曲柄摇杆机构叠加而成，只不过两套机构共用同一曲柄。多数FWMAV目前采用微型电机驱动的曲柄摇杆机构或曲柄滑块机构来实现扑翼运动[34-38]。其优点是运动副为低副，压强较小，可以承受较大的载荷；同时也便于润滑，不易产生大的磨损。为了进一步探明弹性元件引入到FWMAV传动机构中对于电机输入的扭矩及系统能耗的影响，本文采用曲柄滑块机构来作为扑翼飞行器的扑动机构基本构型，在经典FWMAV “Sparrow”飞行器原型基础上展开研究。

首先对4种构型进行动力学理论方面的分析和研究；然后验证理论分析的正确性，分别对4种构型在恒定转速驱动假设下进行仿真，并对4种情况下的峰值转矩进行比较分析；在应用时，由于电机负载很难保持稳定，所以电机转速也会发生波动。为对实践提供参考，进一步采用恒压电机假设对机构进行驱动试验分析，比较4种构型中电机扭矩、功率峰值、电机转速和电流的变化情况。另外，不同构型在各机构运动副的冲击力也接受了考察。

1 扑翼机构动力学方程

图1为美国特拉华大学研制的“Sparrow”扑动机构原理图[4]。OAB是将圆周运动转换为直线往复运动的平面曲柄滑块机构，C和D是带动翅翼上下扑动的滑块机构，该机构结构完全对称，运动也是完全对称。首先在刚性的扑翼传动机构上不安装任何柔性装置，即文中所提到的原构型1。在此基础上提出3种带有弹性元件的刚柔耦合扑动机构模型，分别是：构型2，在翅翼两侧安装弹簧，观察电机的峰值转矩相较于未安装弹簧时的变化情况，如图2所示；构型3，即在系统顶部安装弹簧，观察电机的峰值转矩相较于前面两种构型的变化情况，如图3所示；初步研究发现，前两种安装弹簧的系统都可以在一定程度上减少电机的峰值转矩，为进一步探索组合柔性构型的效果，提出了构型4，即在翅翼两侧和系统顶部同时安装弹簧，如图4所示。

曲柄OA的质量为m1，连杆AB的质量为m2，与连杆连接的滑块的质量为m3，与左、右翅翼连接的滑块质量相同，均为m4，左、右翅翼的质量也相同，均为m5,J1为曲柄的转动惯量，J2为连杆的转动惯量，左、右翅翼的转动惯量相同，均为J3，翅翼两侧的弹簧刚度系数相同，为k1=k2，系统顶部安装的弹簧的刚度系数为k3；a为曲柄OA的长度，b为连杆AB的长度，c为与翅翼相连的滑块和与连杆相连的滑块之间的长度，d为与连杆相连的滑块中心与O点之间的长度，e为与翅翼相连的滑块与O点之间竖直方向的长度，f为与翅翼相连的滑块和与连杆相连的滑块在竖直方向的长度，w为翅翼的长度，R为翅翼弹簧上端连接处与翼根处的长度，P为翅翼弹簧下端与O点之间的长度；θ1为曲柄转角，θ2为连杆与竖直线OB之间的夹角，θ3为翅翼与竖直线OB之间的夹角，θ4与θf相等，均为翅翼与水平线右端之间的夹角。

使用带有约束条件的拉格朗日方程，可得

(1)

式中：λ1、λ2为拉格朗日乘子;x1为与连杆相连的滑块运动的长度，x2为与翅翼相连的滑块运动的长度;并且有

(2)

令

x1=asinθ1

(3)

即

(4)

将式(4)代入式(1)，然后分别对θ1、θ2、θ3进行拉格朗日方程求解，得

(5)

(6)

(7)

τm和τa分别为电机转矩和气动转矩。求得系统的动力学方程可表示为

(8)

式中：

(9)

(10)

(11)

(12)

1) 由于在构型1中未安装柔性装置，所以弹性势能为零，即

(13)

2) 构型2中由于在翅翼两侧位置安装了弹簧，所以存在弹性势能，当翅翼处于水平位置时，弹簧为原长，此时弹性势能为零，在整个运动过程中，弹簧的伸长量为

ΔI1=

(14)

增加的弹性势能为

(15)

所以

g2(θ)=

(16)

其中：

M=1+

(17)

3) 构型3在系统顶部安装了弹簧，当翅翼处于水平位置时，弹簧为原长；运动过程中,弹簧的伸长量为

ΔI2=ccosθ3

(18)

增加的弹性势能为

(19)

所以，

(20)

4) 构型4在翅翼两侧和系统顶部均安装弹簧，当翅翼处于水平位置时，弹簧为原长；运动过程中,翅翼两侧弹簧的伸长量为

ΔI1=

(21)

系统顶部的弹簧伸长量为

ΔI2=ccosθ3

(22)

增加的弹性势能为

(23)

所以，

(24)

2 翅翼气动力矩

如图5所示，为了方便计算翅翼的气动力矩，将翅翼平面离散成一个个微小的微元，这样就可以在离散网格上得到相应的速度和压力元[39-40]。dF为微元上的气动升力。对翅翼表面的压力和黏性元进行积分，可以获得翅翼平面上受到的空气动力力矩[41-42]。在非稳态气流状态下翅翼平面上的微元所受的空气动力力矩与稳态气流下的相同[43]。在翅翼平面坐标系下，力矩在翅翼平面坐标系中可以分解为3个分量，即相对于翅翼平面的法向力矩、展向力矩和弦向力矩[44-46]。每个翼面微元上所产生的力矩可表示为

(25)

(26)

(27)

对式(25)～式(27)积分可得

(28)

(29)

(30)

式中:ML、MM、MN为翅翼平面坐标系下的3个空气动力力矩分量；cL、cM、cN分别为沿翅翼平面法向、展向和弦向的动力矩系数；r为翅翼平面上的点到扑翼飞行器质心的距离；c1为平均气动弦长；u(ξ,ψ,ζ)为翅翼运动的角度大小；v(vx,vy,vz)为扑翼飞行器的速度大小；ω(f,θ,φ)为扑翼飞行器的姿态角；ρ为空气密度；U为参考速度;S为翅翼面积。

以上各力矩在飞行器体坐标系中可表示为

MB=TB(ML,MM,MN)T

(31)

式中:TB所表示内容为飞行器翅翼坐标系和体坐标系之间的坐标变换，如式(32)所示：

(32)

基于气动分析，可以计算出“Sparrow”扑翼飞行器在运动过程中翼面所受到的气动力矩[31]。

得到气动力在一个拍动周期内随曲柄转角的变化曲线，如图6所示。

3 机构仿真分析

为了定量研究弹簧的引入对于电机输入扭矩需求等因素的影响，在仿真实验部分采用输入电机恒定转速方法[47]对各构型在悬停飞行模式下的扑动进行研究。基于恒速假设，确保各构型实现与未加弹簧的“Sparrow”原型相同的气动过程(见图6)，需要使所有构型的各连杆和滑块的位移、速度、加速度的变化一致。在此条件下，就能比较在弹簧增加前后所需的电机输入扭矩变化情况。恒速假设下，使构型的改进只影响输入(扭矩)，而确保输出(扑翼运动及相应气动情况)不变，故构型变化将不对气动因素产生影响。

各构型中与连杆相连的滑块B是扑动机构与翅翼连接的部分，通过研究其运动可以反映翅翼的扑动情况。根据“Sparrow”模型[46]，扑翼机构的各部分尺寸分别为a=1 cm,b=4 cm,c=1.414 cm,e=4 cm,P=1.2 cm,w=30 cm,c1=3 cm。图7所示为与翅翼相连的滑块由扑动最高点运动到最低点，再由最低点运动到最高点一个周期内的位移、速度和加速度随时间的变化曲线。在恒速假设下，通过仿真得到了一个周期内4种构型相同的滑块运动情况。由于构型中弹簧的引入，电机实现相同运动所应提供的电机输入扭矩可从图8～图15及表1得到。

1) 构型1：未安装弹簧

从图8转矩和翅翼扑动角随时间的变化曲线可以看出，“Sparrow”在图示周期内0～0.1 s时，翅翼进行下拍运动，转矩开始为正值，即由电机向系统输入能量，驱动翅翼向下拍动；当翅翼快要下拍到最低点时，转矩变为负值，电机做负功，即电机从系统中吸收能量。0.1～0.2 s翅翼进行上拍运动，转矩为正值，电机做正功，电机向系统输入能量，后半程的时候，转矩为负值，电机做负功，电机从系统中吸收能量。同时，从图8中也可以看出，在进行下拍运动过程中，转矩为正值的时段比转矩为负值的时段长，即电机向系统输入能量的时间比电机从系统中吸收能量的时间长。这是因为翅翼受到气动力的作用，在下拍运动的过程中，气动力对系统做负功，电机要克服气动力做功的影响。在上拍运动的过程中，转矩为正值的时段比转矩为负值的时段短，即电机向系统输入能量的时段比电机从系统吸收能量的时段短，这是因为在进行上拍运动的过程中，气动力对系统做正功，从而使得电机做功减少。

对比图7位移、速度、加速度随时间的变化曲线图，当翅翼在进行下拍运动到达最低点时，系统的动能由最大值减小到零，同时转矩突然由负值变为零，表明当翅翼在进行下拍运动的后半程到达最低点的过程中，系统存在着一部分的动能损失。同理，当翅翼在上拍运动的后半程到达最高点的过程中，同样存在着一部分的能量损失。为了减小这一过程中的能量损失，引入了弹簧元件进行分析和比较。

2) 构型1和构型2比较

如图9所示，当在翅翼两侧安装弹簧，同时弹簧刚度选取合适的值时，可以明显减小系统所需的电机转矩峰值，经过优化分析可得，当弹簧刚度k1=k2=0.09 N/mm时，可以最大限度地减小电机的转矩峰值。和没有安装弹簧时电机的转矩变化曲线进行比较，未安装弹簧时，系统的转矩峰值为98.721 7 N·mm，安装弹簧后，系统的转矩峰值为77.8787 N·mm,转矩峰值的减小量为20.843 N·mm，减小的百分比为21.11%。

3) 构型1和构型3比较

图10所示是构型1和构型3翅翼在一个运动周期内转矩的变化曲线。可以看出，构型3相较于构型1可以明显减小驱动时的电机转矩峰值。经过优化分析，当k3=1.1 N/mm时，峰值转矩变化最明显。未安装弹簧时，系统的转矩峰值为98.721 7 N/mm，在系统顶部安装弹簧后，系统的转矩峰值为60.710 6 N/mm，转矩峰值的减小量为38.011 1 N/mm，减小的百分比为38.5%。综合扑翼飞行器上拍和下拍的整个运动周期，当k3=1.1 N/mm时，所需要的转矩峰值最小，可以最大限度地降低电机的输入转矩峰值，减小电机的额定转矩。

4) 构型1和构型4比较

由以上3种情况分析可知，给扑翼机构两侧翅翼或者系统顶部安装弹簧都可以减小翅翼运动过程中电机的峰值转矩。为了探究两种柔性构型的组合效果，作者对构型4的弹簧取不同刚度值进行了仿真分析。

如图11～图13所示，蓝色曲线均为未安装弹簧时系统的转矩变化曲线。从图中可以看出，在以上3种不同的组合中，均能找出一个转矩峰值减小量最大的曲线，分别将转矩峰值减小量最大的曲线提取出来，进行比较，以找出最优曲线。

图14所示为k1=k2和k3分别取不同刚度值时最优转矩的变化曲线，从图中可以看出，当k1=k2=0.08 N/mm，k3=0.2 N/mm时，转矩峰值的减小量最大。此时，转矩峰值为71.318 6 N/mm，转矩峰值的减小量为27.403 1 N/mm，减小的百分比为27.76%。为两种构型的弹簧进行组合取不同刚度值时转矩的最优值，如图14红色曲线所示。

Table1Comparisonofpeaktorquesoffourtypesofconfigurations

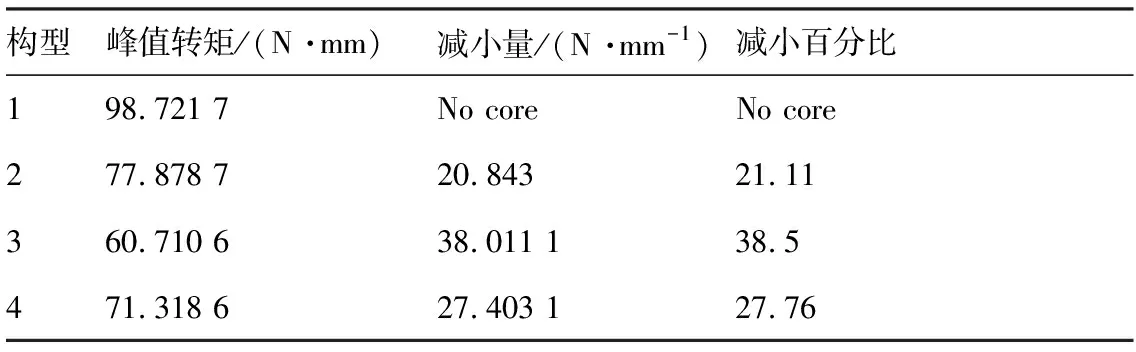
构型峰值转矩/(N·mm)减小量/(N·mm-1)减小百分比198.721 7No coreNo core277.878 720.84321.11360.710 638.011 138.5471.318 627.403 127.76

5) 全构型比较

图15所示为构型1、构型2、构型3、构型4转矩变化取得最优值时的比较曲线。从以上4种构型的转矩变化曲线和表1进行比较分析可得，构型3，即在系统顶部安装弹簧时，峰值转矩的减小量最大，减小的百分比为38.5%。其次是构型四，减小的百分比为27.76%。构型2，即在翅翼两侧安装弹簧时，转矩峰值的减小量最小，减小的百分比为21.11%。因此，可以出这样的结论，在扑翼系统安装弹簧的3种扑动机构构型中，在系统顶部安装弹簧时，可以最大限度地减小转矩峰值，对电机额定转矩的减小效果也最明显。

4 试验分析

在实际应用中，由于负载不是恒定不变的，因此很难保证恒速驱动。为了与实际情况更加吻合，进一步采用恒定电压驱动的方式来研究弹性元件对于输入扭矩的实际改善效果。在恒压假设下，通过在曲柄转动轴的位置安装一直流电机进行驱动。此法将便于后续物理实验的开展和数据分析。在直流电机的驱动下，通过观察和比较不同构型的电机输入转矩、转速、功率和电流的变化，可分析各系统所消耗的能量大小，进而得出能量消耗最小的构型。

直流电机可以抽象为一个简单电路模型[48-49]，该模型考虑了电机电枢电阻、电机电枢电感和电机电枢的反电动势。对该电路模型，可用基尔霍夫电压定律列出电动势平衡方程：

(33)

式中:Um为施加在电机上的电压；Em为电机电枢的反电动势；Rm为电机电枢电阻；Im为流过电机电枢的电流；Lm为电机电枢电感。

此外，直流电机还要满足：

τm=KtIm

(34)

Em=Kewm

(35)

(36)

式中:τm为电机转矩，顺时针方向旋转；Kt为电机转矩系数；Ke为感生电动势系数；wm为电机电枢的角速度；TL为负载转矩，亦即曲柄转矩，顺时针方向；Jm为转动惯量。在国际制单位中，Kt=Ke。电机选用并励直流电机，由于FWMAV采用的微电机其额定电压一般都是1.5 V或3 V，在额定电压下电机的输出转矩难以满足实际需要,因此在FWMAV中普遍采用了提高电机的输入电压来增大微电机的输出转矩[39]，为了保持与第3节机构仿真分析过程中的周期相近，此处选用接近实际电机产品额定电压的电压参数设置，即设定源电压为50 V，电枢电阻、单级磁通、级数和比例因子等电机参数均采用系统默认参数设置。具体电机相关参数如表2所示。

图16～图19及表3所示为恒定电压驱动下4种构型中电机的转矩、功率、转速和电流随时间的变化曲线。

由图16转矩的变化曲线进行比较分析可以得到，构型1～4的最大峰值转矩分别为101.538 6、79.040 1、63.068 7、74.146 4 N/mm，转矩减小的百分比分别为22.16%、37.89%、26.98%。从图17功率变化曲线比较分析可以得到，4种构型的功率峰值分别为3.188 5、2.482 3、1.980 8、2.328 6 W，功率峰值减小的百分比分别为22.15%、37.88%、26.97%。从表3转矩和功率峰值的减小百分比可以看出，构型3，即在系统顶部安装弹簧的机构，转矩和功率峰值的减小量最大，可以最大限度地降低电机转矩和功率。

从图18转速变化曲线和表3分析可以得出，4种构型中转速的波动范围大小分别为0.260 8、0.205 7、0.160 2、0.190 5 r/min。经过比较分析可知，构型3电机转速的波动范围最小，电机转速也更加稳定。从图19电流变化曲线分析可以得到，4种构型的电流峰值分别为0.063 8、0.049 7、0.039 6、0.046 6 A，减小的百分比分别为22.10%、37.93%、26.96%。经过比较分析可得，构型3中电机的电流峰值减小量最大，在电机电阻和电感上损耗的功率也最少，能量的利用率也最高。

表2 电机相关参数Table 2 Parameters of motor

Table3Comparisonofparametersofmotorsoffourconfigurations

构型峰值功率减小百分比峰值转矩减小百分比转速波动/(r·min-1)峰值电流减小百分比1No coreNo core0.260 8No core222.15%22.16%0.205 722.10337.88%37.89%0.160 237.93426.97%26.98%0.190 529.96

5 运动副反力

由前面的仿真和试验对比分析可知，给系统增加弹簧后，会减少电机输入的转矩峰值，在机构各连接位置分别安装力传感器[50]，发现不安装弹簧和安装弹簧时，各运动副所受的冲击力也发生了明显的变化。图20～图24是4种构型中各运动副处的受力情况。其中，JOINT_1为电机和曲柄之间的旋转副，JOINT_2为曲柄和连杆之间的旋转副，JOINT_3为连杆和滑块之间的旋转副，JOINT_11，JOINT_12分别为左、右两侧翅翼与竖直方向运动的滑块之间的旋转副，JOINT_13、JOINT_14分别为左、右两侧翅翼与两侧水平运动滑块之间的旋转副，其他的运动副由于受力较小，不予考虑。

由图20～图23中力的曲线可以看出，无论哪种构型，运动副JOINT_1和JOINT_2中的力始终最大。因此，可以得出，在4种构型中，可以通过研究JOINT_1和JOINT_2其中一个运动副处的力的变化来观察不安装弹簧和安装弹簧后运动副处的受力变化情况。如图24所示，将4种构型运动副中受力最大的运动副JOINT_1提取出来进行比较。

如图24所示，构型1中运动副受力的最大值为36.580 7 N，构型2中运动副受力的最大值为27.630 3 N，构型3中运动副受力的最大值为26.522 6 N，构型4中运动副受力的最大值为26.049 2 N。和不安装弹簧的构型相比，有弹簧的各构型运动副中最大受力分别减小了8.950 4 N，10.058 1 N，10.531 5 N。其中，构型4可以最大限度地减少各运动副所受到的力，其次是构型3。

综合而言，构型3不仅可以最大限度地减小峰值转矩，而且还可以较好地降低运动副中受到的冲击力，进而可以减小运动副中的冲击和振动。

6 结 论

在扑动机构无弹簧时，翅翼在下拍到最低点或是上拍到最高点时，由于速度的突变，能量会发生一部分的损失，增加弹簧后，其中一部分原本应该损失的能量因为弹簧的作用，作为弹性势能储存在弹簧系统中，当翅翼由最低点进行上拍或是由最高点进行下拍的时候，储存在弹簧系统中的弹性势能则向系统输入能量，从而抵消了一部分应该由电机向系统输入的能量，使得电机的转矩峰值得以减少，进而达到降低电机转矩峰值的目的。总的来说，弹簧存在的作用是将原本应该损失的能量有效地利用和储存了起来，至于在中间运动过程中克服弹簧力虽然会增加能量消耗，但是这一部分增加的能量也会在之后的运动过程中释放出来，在一个运动周期过程中相当于并未增加能量消耗。

进一步研究得到了各构型转矩减小量最大时的弹簧刚度值。经比较发现：在机构顶部安装弹簧时对电机的峰值转矩减小最大。此后，最优刚度构型的恒定电压试验比较了从电机输入的转矩峰值、功率、电流和转速的变化。结果显示：在扑动机构上安装弹簧等柔性元件可以有效降低电机输入的峰值转矩和峰值功率，提高能量利用效率。另外，扑动机构中柔性元件的引入可以显著降低运动副处的冲击力，从而达到减震和降噪的目的，在一定程度上延长了机构的使用寿命。