加速退化模型及外推结果准确度的定量验证方法
2018-09-29周源王浩伟盖炳良
周源,王浩伟,盖炳良
1. 海军航空大学 3院,烟台 264001 2. 海军工程大学 兵器工程学院,武汉 430032
掌握产品的可靠度变化规律对于有效开展预防性维修、避免装备的灾难性故障至关重要,开展可靠性试验是获取产品可靠度变化规律的重要途径[1]。传统的可靠性试验是通过获取产品的失效时间数据推断可靠性指标,这种方式的可靠度评估精度相对较高,然而试验时间较长。当今社会的产品更新换代加快,对可靠性试验的时效性要求很高,传统的可靠性试验在时效性方面难以满足产品研发需求。为了提高可靠性试验的效率,可靠性试验发展了性能退化试验类型,针对某些性能参数缓慢劣化最终导致失效的产品,通过对性能参数退化量的变化规律进行准确建模,勿需产品失效即可预测出产品的失效时间[2-4]。某些性能退化产品的性能退化速率受温度、电压、振动等环境应力的影响,提高环境应力水平可以加速产品的性能退化过程,从而进一步缩短可靠性试验的时间,根据此原理又发展了加速退化试验类型[5-7]。
目前对加速退化试验的研究主要集中在退化试验方案优化设计[8-9]和加速退化建模[10-11]两大方向,但对于加速退化模型与外推结果的验证方法缺少深入研究,尚未形成一套较为科学的验证方法。加速退化试验本质上是牺牲部分可靠度评估精度换取可靠度评估效率,外推到常应力下的可靠度结果通常会与真实值存在一定的偏差,因此需要验证此偏差是否在可接受的范围内。考虑到产品可靠度的真实值无法直接测量得出,可利用常应力下的可靠性数据建立验证标准。Zhang等[12]在开展某型发光二极管加速退化试验时,利用常应力下的性能退化数据建立了产品平均寿命的验证标准,通过比对加速试验外推的平均寿命值与验证标准值,定性验证了外推结果的准确性。然而,工程实践中往往难以获取常应力下的可靠性数据,这是验证工作经常面临的难题[13]。针对此情况,Yao等[14]将最低加速应力水平下的退化数据作为验证标准,验证外推到低加速应力下可靠度结果的准确性。另外一些研究工作将加速退化模型与加速退化数据的拟合优劣作为验证标准,例如Ling等[10]基于Gamma随机过程建立了3种加速退化模型用于预测发光二极管剩余寿命,认为拟合最优的加速退化模型具有最准确的外推结果;Wang等[15]对碳膜电阻器加速退化数据进行统计分析,通过比较AIC(Akaike Information Criterion)值判断各加速退化模型的拟合优劣。以上研究工作实现了预测评估结果的定性验证,但并没有提出有效的定量验证方法,验证结论缺乏说服力。
Ling和Mahadevan[16]归纳总结了预测模型的各类定量验证方法,将其分为假设检验法和非假设检验法两大类,具体包括经典假设检验法、Bayesian假设检验法、可靠性指标法、面积指标法4个分支。许丹等[17]提出了一种常应力下性能退化模型的验证方法,结合波动阈值一致性检验与空间形状相似性一致性检验进行验证。然而,以上只是研究了常应力下预测模型与预测准确度的验证方法,不能解决加速退化模型与外推结果的准确度验证问题。为了提供一套较为科学的加速退化模型与可靠度评估结果的验证方法,本文首先根据可靠性建模的步骤设计了验证流程,然后结合Wiener-Arrhenius加速退化模型构建了验证技术框架,并通过实例应用展现了技术框架的可行性与有效性。
1 验证流程
通过加速退化试验可以高效获取产品在多个应力水平下的性能退化数据,从而建立产品的加速退化模型,进而外推出产品在常应力水平下的可靠度模型,基于加速退化数据的可靠度评估流程如图1所示。由于错误建立的性能退化模型结合错误建立的加速模型在某些情况下的外推结果也比较接近真实值,验证外推结果准确度之前需要首先验证所建立各模型的合理性。根据以上分析,设计了加速退化模型及外推结果准确度验证流程(见图1)。
本文在以上验证流程的基础上构建了一套验证技术框架,包括基于假设检验的模型验证方法,及基于面积比的外推结果验证方法,以下结合Wiener-Arrhenius加速退化模型对验证技术框架进行阐述。
2 Wiener-Arrhenius加速退化模型
对于大多数产品来说,掌握其失效机理并据此建立失效物理模型是比较困难的,特别是对于缺乏可靠性信息的新型产品更是如此,目前在建立退化失效型产品的可靠度模型时大都采用基于退化数据拟合的建模方法[18]。Wiener等连续时间随机过程模型不仅具备优良的统计特性,而且适合描述产品退化的不确定性,因此被广泛用于性能退化建模。利用加速退化数据推导产品在常应力下的可靠度模型,首先要建立产品的性能退化模型。假定某产品的性能参数具有退化特点并且其性能退化量Y(t)服从Wiener过程,则可将Y(t)表示为
Y(t)=μΛ(t)+σB(Λ(t))
(1)
式中:μ为漂移参数;σ>0为扩散参数;Λ(t)=tΛ为关于时间的函数,Λ为形状参数;B(·)为标准布朗运动[19-20]。产品性能参数的退化速率与温度、电压、振动、湿度等因素有关,反映在性能退化模型中为模型参数μ、σ、Λ中的至少一个与环境应力相关,与环境应力相关的参数可利用加速模型描述参数值与应力水平之间的关系[21]。然而,目前普遍根据工程经验或主观判断假定哪些模型参数与环境应力相关,应用最广泛的假定为μ与环境应力相关而σ、Λ与环境应力无关[22-23],另一种应用较多的假定为μ、σ与环境应力相关而Λ与环境应力无关[24-25],文献[26]证实采用此两种假定获取的可靠度评估结果具有较大差异。为了避免以上假定的风险,文献[26-27]采用加速因子不变原则推导出μ、σ与环境应力相关而Λ与环境应力无关,并且μ、σ值应该随应力水平呈比例变化。据此以绝对温度T为协变量,对μ、σ建立基于Arrhenius方程的加速模型,具体表达式为
μ(T)=exp(γ1-γ2/T)
(2)
σ(T)=exp(γ3-0.5γ2/T)
(3)
式中:γ1、γ2、γ3为待估系数。进而建立Wiener-Arrhenius加速退化模型为
Y(t;T)=exp(γ1-γ2/T)tΛ+
exp(γ3-0.5γ2/T)B(tΛ)
(4)
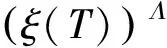
(5)
进而推导出产品的可靠度模型为
exp(2Dexp(γ1-2γ3))·
(6)
式中:Φ(·)为标准正态分布函数。
为了确定产品的可靠度模型,需要估计出模型参数向量θ=[γ1γ2γ3Λ]。根据Wiener过程的统计特性,独立增量ΔY(t;T)服从如下形式的正态分布:
ΔY(t;T)~N(exp(γ1-γ2/T)ΔΛ(t),
exp(2γ3-γ2/T)ΔΛ(t))
(7)
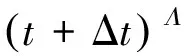
(8)
以上介绍了Wiener-Arrhenius加速退化模型建立方法及参数估计方法,同样可以结合Eying、Power law等加速模型建立Wiener-Eying,Wiener-Power law加速退化模型。
3 加速退化模型验证方法
3.1 基于加速退化数据的验证方法
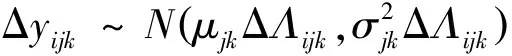
(9)
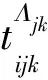
(10)
则说明此产品的性能退化数据服从Wiener退化模型。设零假设为H0:式(10)成立;备选假设为H1:式(10)不成立,可采用Kolmogorov-Smirnov检验法、Anderson-Darling检验法等验证式(10)是否成立。显著性水平设为α=0.05,当p≥α时不能拒绝零假设,认为产品的性能退化数据服从Wiener退化模型,否则认为产品的性能退化数据不服从Wiener退化模型。Kolmogorov-Smirnov检验法与Anderson-Darling检验法的p值计算方法见文献[30-31]。
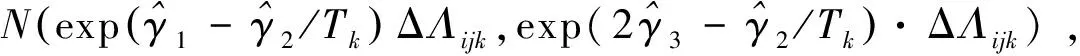
(11)
所用到的假设检验方法亦为Kolmogorov-Smirnov检验法、Anderson-Darling检验法。
3.2 基于常应力可靠性数据的验证方法
随着时间的推移,能够累积一些产品在常应力下的可靠性数据,将这些可靠性数据作为标准对建立的加速退化模型进行准确度验证。产品在常温度水平T0下的可靠性数据分为3种情况:① 仅有失效时间数据;② 仅有性能退化数据;③ 同时具有性能退化数据与失效时间数据。针对此3种情况分别提出验证方法:
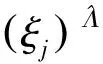
(12)
则说明建立的加速退化模型是准确的。采用Anderson-Darling检验法验证式(12)是否成立。
2) 设产品在T0下的性能退化数据为yij、tij(i=1,2,…,H;j=1,2,…,N),设
(13)
如果zij服从标准正态分布,则说明建立的加速退化模型是准确的,采用Anderson-Darling检验法验证式(13)是否成立。
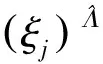
4 外推结果验证方法
4.1 建立标准可靠度模型
1) 设产品在常温T0下的失效时间数据为ξj(j=1,2,…,J),由逆高斯分布建立标准可靠度模型为
(14)
(15)
式中:δ为逆高斯分布的均值参数;λ为逆高斯分布的尺度参数。
2) 设产品在常温T0下的性能退化数据为yij、tij(i=1,2,…,H;j=1,2,…,N),建立标准可靠度模型为
(16)
(17)
3) 设产品在T0下同时具有失效时间数据ξj与性能退化数据yij、tij,建立标准可靠度模型为
(18)
(19)
4.2 基于面积比的定量验证
利用加速退化数据外推得出的产品在T0下的可靠度模型记为
设利用加速退化数据外推出的可靠度曲线R(t;T0)与标准可靠度曲线R(3)(t)如图2所示。
文献[16]利用两种可靠性曲线之间的面积表征可靠度评估结果的累计误差,如图3中展示的红色区域,计算公式为
s(R(t;T0),R(3)(t))=
s(R(t;T0),R(3)(t))虽然能够定量给出外推可靠度结果的误差,然而难以据此做出外推结果是否准确的判断。为解决此难题,提出利用面积比r定量表征外推结果的相对误差,并且指定一个阈值ε,如果r≤ε则认为外推结果是准确的。r的计算公式为
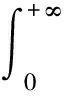
步骤1选取一个较大的横坐标值,如t*=2 000,使得R(t*;T0)=0,R(3)(t*)=0。
步骤2每次通过设t=UNI(0,t*),R=UNI(0,1)(UNI表示均匀分布),在图2所示的绿色区域内选一个随机点(t,R)。
步骤3判断(t,R)是否落入R(3)(t)与横坐标之间的区域(图3的蓝色区域)或R(t;T0)与R(3)(t)之间的区域(图3的红色区域)。
步骤4执行步骤2和步骤3共计L次,统计(t,R)落入蓝色区域的次数K1,及落入红色区域的次数K2;当L足够大的时候,如下关系式成立:
(20)
(21)
(22)
以上工作是验证整条可靠度曲线的准确性。工程实践中在某些情况下更看重可靠度曲线的上半部分是否准确,从而能够更精确地计算出产品t0.9、t0.8等可靠寿命,根据此需求可建立如下验证模型
(23)
式中:t0.5由R(3)(t0.5)=0.5计算得出。
5 案例分析
某惯导系统伺服电路在长期贮存过程中具有性能退化现象,表现为电路电压逐步降低,根据产品设计规范,伺服电路的电压测量值x相对于初始值x0的相对百分比变化量y=100|x-x0|/x0到达失效阈值D=10时,产品失效。温度的长期作用能够导致伺服电路的电路参数漂移、磁性减弱,是伺服电路电压值降低的主要环境敏感应力。伺服电路电压在常温T0=298.16 K下的退化过程较为缓慢,为了高效评估出此产品的可靠性,设计了温度应力加速退化试验用于加速产品的退化过程。随机抽取的22个试验样品被分配到3组加速温度(T1=323.16 K,T2=348.16 K,T3=368.16 K)下进行加速退化试验,各温度下样品的退化数据y如表1~表3所示,表中#1~#22为样品编号。
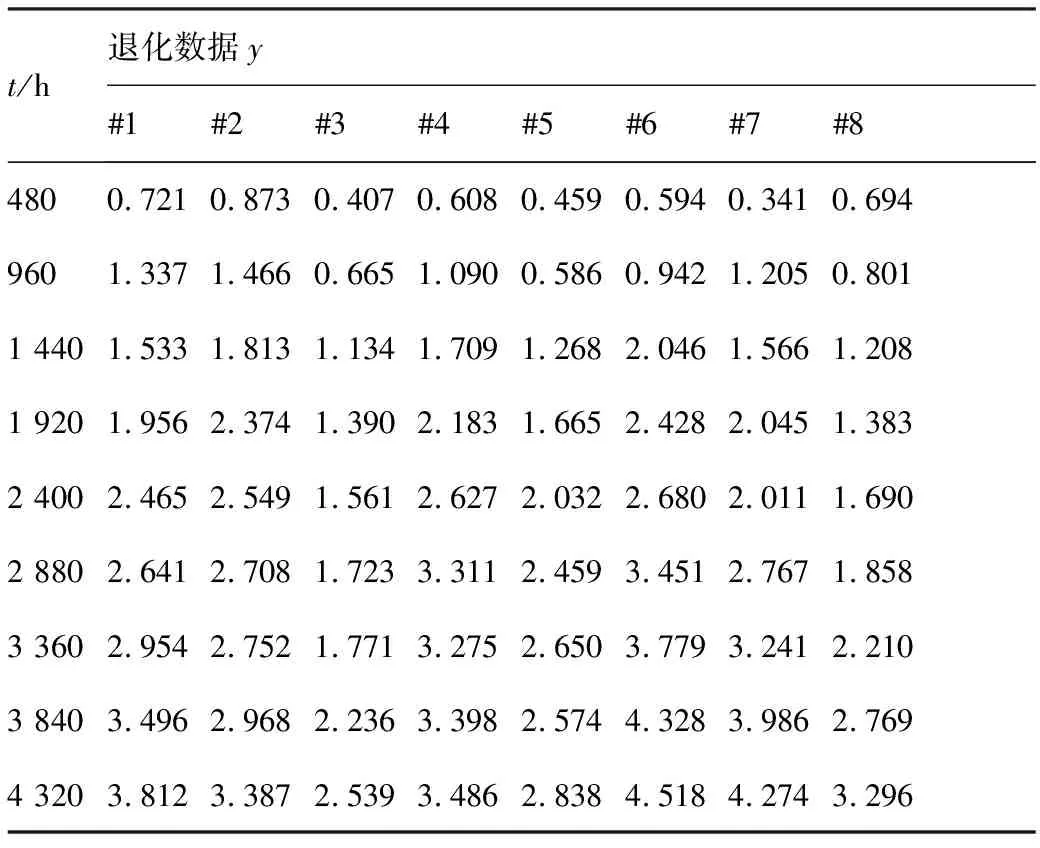
表1 T1下样品的退化数据Table 1 Degradation data of samples under T1
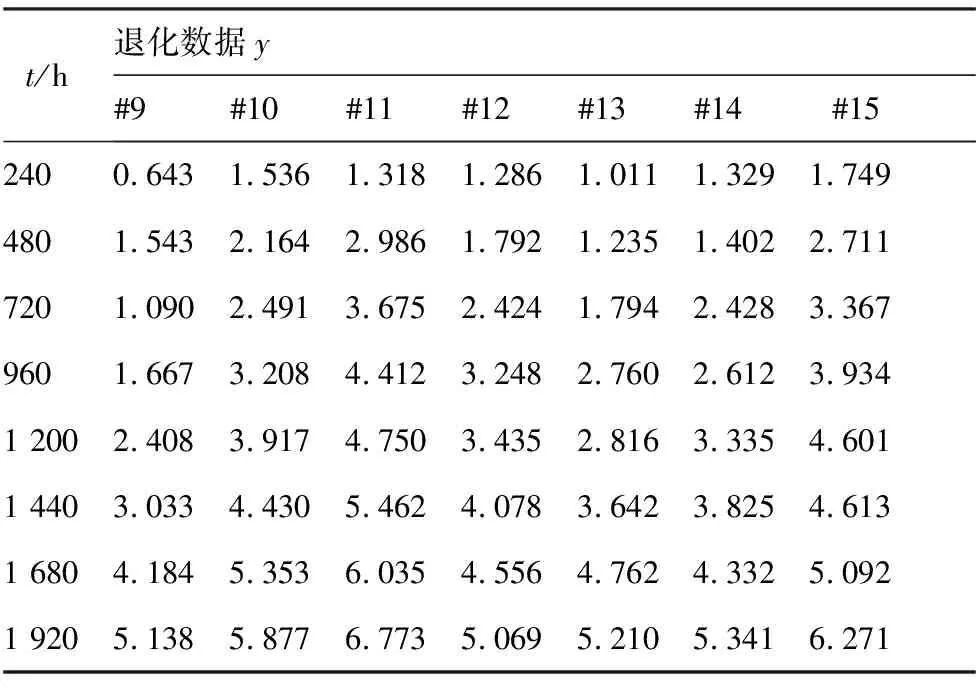
表2 T2下样品的退化数据Table 2 Degradation data of samples under T2
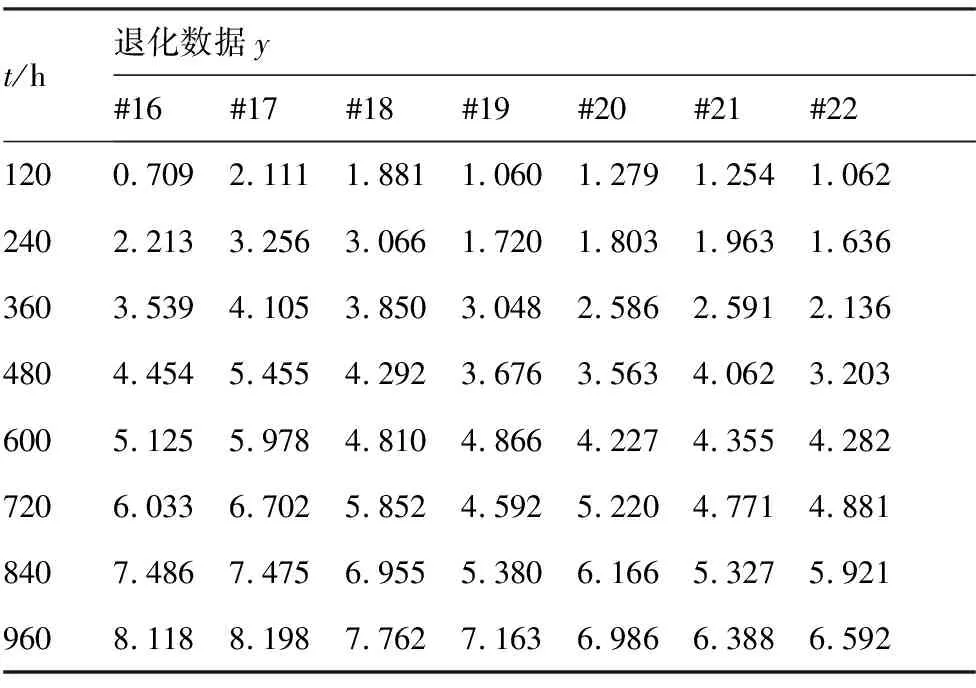
表3 T3下样品的退化数据Table 3 Degradation data of samples under T3
5.1 基于加速试验数据的加速退化模型验证
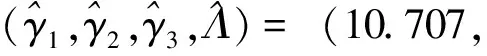
5.2 基于常应力可靠性数据的加速退化模型验证
收集了4个产品在T0下的失效时间数据为ξj=70 070,65 836,87 609,80 803 h以及2个产品在T0下的性能退化测试数据,如表4所示。
首先利用Anderson-Darling检验方法验证ξj是否满足式(12)指定的关系式,计算得p值为0.431,在显著性水平α=0.05下不能拒绝关系式(12)成立的零假设;然后利用Anderson-Darling检验方法验证表4中两个产品的性能退化数据是否满足zij~N(0,1),被检样本zij对标准正态的拟合情况如图5所示,计算得p值大于α,也不能拒绝关系式成立的零假设,说明所建立的加速退化模型通过常应力可靠性数据的验证。
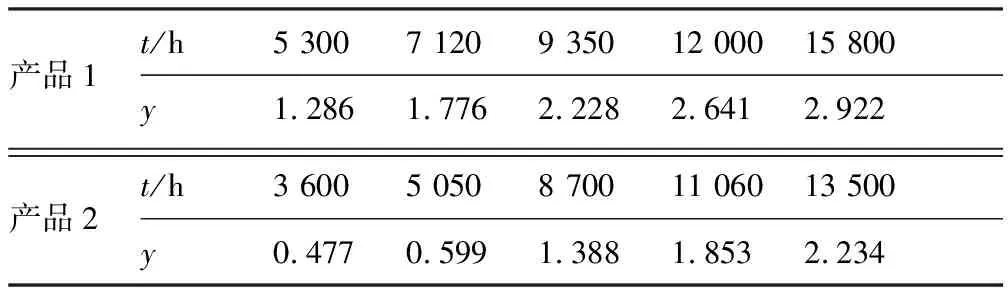
表4 常温下退化数据Table 4 Degradation data under normal temperature
5.3 基于常应力可靠性数据的评估结果验证
5.4 对其他Wiener-Arrhenius加速退化模型的验证
标准可靠度曲线R(3)(t)与外推出的可靠度曲线R*(t;T0)如图8所示,计算出两类面积比为r>45.45%,远大于阈值ε=0.2,说明此外推的可靠度结果不准确。
6 结 论
1) 设计了加速退化模型及外推结果准确度验证的技术流程,结合Wiener-Arrhenius加速退化模型构建了具体的验证技术框架,通过实例应用展现了技术框架的可行性与有效性,为解决加速退化试验中的验证问题提供了重要参考。
2) 提出了基于假设检验的模型验证方法,利用Kolmogorov-Smirnov检验法、Anderson-Darling检验法能够客观、科学地验证建立的Wiener-Arrhenius加速退化模型是否合理、准确。
3) 提出了基于面积比的外推结果验证方法,利用蒙特卡罗仿真解决复杂可靠度函数积分问题,用于定量表征外推结果的准确度,通过面积比阈值判定是否接受外推结果,此方法具有较好的工程实用价值。
4) 研究工作为解决加速退化试验中的验证难题做出了有益的探索,所设计的验证技术流程及各种定量验证方法具有一定的理论价值。
