基于贝叶斯网络的自由场地震液化沉降评估

唐小微, 白 旭， 胡记磊

(1.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116023；2. 华中科技大学 土木工程与力学学院，武汉 430074)

地震液化引起地基沉降导致的地下或地上结构物的破坏是液化灾害的一种表现形式。在地震液化后，随着液化土层的超孔隙水压力消散，土颗粒的重新排列会导致地基土排水再固结，出现地基土下沉现象，从而引发地基承载力失效，导致地下或地上结构物破坏，如1964年日本新泻Mw7.5级地震中因地基液化导致的沉降灾害严重，最大沉降量高达约3.8 m，导致大量房屋损坏、倾斜，甚至倒塌[1]；1999年中国台湾集集Mw7.6级地震中彰化滨海工业园鹿港西二区发生严重液化，导致地表沉降达0.33～0.45 m[2]；2011年日本东北地区太平洋近海岸Mw9.0级地震，导致东京地区的液化沉降均在0.3～0.5 m，最严重的液化沉降量高达约1 m，造成大量房屋、桥梁和地下工程设施破坏，带来了巨大经济损失[3]。

地基沉降通常分为软土塑性变形、非饱和砂土震密引起的沉降和饱和砂土液化后再固结引起的沉降，本文只考虑饱和砂土液化发生后沉降评估的相关研究。液化后的沉降评估方法大致可以分为三类：①基于室内试验或现场数据建立的简化评估法；②考虑地震液化沉降的不同影响因素及其非线性和不确定性的机器学习方法；③数值模拟方法。其中，简化算法以Tokimatsu & Seed法[4]和I & Y(Ishihara & Yoshimine)法[5]为代表的两种方法都是基于地基土沉降与砂土的密实度和地震的最大剪切应变的关联为基础，建立的经验模型，其计算简单快捷，但计算粗略，容易导致计算结果的精度较低，且无法考虑液化喷砂冒水引起的水土流失、土骨架破坏和土体介质不连续等因素影响，适用范围较窄。叶斌等[6]对这两种经验模型进行了对比分析，发现分层计算的沉降趋势基本一致，但最终的沉降计算结果存在较大差异，造成这种差异的原因是两种模型的基础试验数据不同。数值模拟方法的准确性主要依赖于精确的场地参数和地震参数以及本构模型的优劣，而且其计算成本较大，一般用于一些重大工程问题。而机器学习方法可以综合考虑砂土液化和地基沉降的众多影响因素及其不确定性、较准确地评估地震液化后地基的沉降量，但该方法是一种单纯的数学方法，很难从地基液化沉降的诱发机理上解释评估结果。具有代表性的研究成果有：Cetin等[7]基于大量循环三轴试验结果、简单剪切试验结果和扭剪试验结果采用线性回归和最大似然方法，建立了评估液化后排水的残余体变和残余剪应变的概率经验模型；陈国兴等[8]基于我国海城地震、唐山地震和日本新泻地震的液化震害数据采用神经网络建立液化沉降预测模型；郭小东等[9]基于遗传算法和回归型支持向量机方法考虑了液化震陷的9个主要影响因素建立了评估模型。这些方法因选取的影响因素不统一和不全面，未考虑不同土类和场地特性的影响，故预测结果不理想，仍需要进一步提高其综合泛化能力。

贝叶斯网络方法适用于表达和分析不确定性和概率性的事件，可以从不完全、不精确或不确定的知识或信息中做出准确的推理，特别适用于像地基液化沉降这样有条件地依赖于多种控制因素的高度非线性复杂问题。贝叶斯网络已被广泛地应用于医学、军事、信息和灾害风险等领域，也逐渐应用在地震液化预测等问题中，如Bayraktarli[10]将改进的Seed简化法应用到贝叶斯网络中对1999年Kocaeli地震液化进行了预测；Huang等[11]利用贝叶斯网络考虑液化参数不确定性讨论了模型不确定性对液化预测结果的影响；Hu等[12]综合考虑了地震参数、土体参数和场地条件，建立了地震液化的贝叶斯网络模型，并与神经网络方法对比，验证了该模型的正确有效性。本文在Hu等建立的地震液化贝叶斯网络预测模型的基础上，引入地基沉降参数及其影响因素，扩展该模型，从而建立地震液化后地基沉降的贝叶斯网络评估模型，并与传统的简化计算方法(如I & Y法)和径向基函数(Radial Basis Function, RBF)人工神经网络模型进行对比，利用多个评估指标验证该贝叶斯网络评估模型的精确有效性。

1 贝叶斯网络方法简述

贝叶斯网络(Bayesian Network, BN)是一种用于描述变量之间不确定性因果关系的概率图推理模型，是目前不确定知识表达和推理领域最有效的理论模型之一[13]。它由节点(表示变量)、有向连线(表示变量因果关系)和概率表(表示不确定性)组成，其可以将先验知识和历史数据巧妙地结合起来，对数据进行量化评价。贝叶斯网络是基于贝叶斯理论发展起来的一种图概论方法，其推理准则包括[14]

(1)

P(x1,…,xn)=P(x1)P(x2|x1)…P(xn|x1,x2,…,xn-1)

(2)

(3)

式中：P(Y)为先验概率；P(X|Y)为Y发生时X发生的概率；π(xi)为变量Xi的父亲节点集合。

图1为地震液化引起沉降的一个贝叶斯网络通用模型，包括：①输入节点，如土体参数(SP)、地震参数(EP)和场地条件(FC)；②状态节点，如液化势(LP)和液化潜能指数(LP)；③输出节点，如沉降量(S)。

图1 地震液化引起的沉降灾害通用贝叶斯网络模型Fig. 1 A generic BN model of seismic liquefaction-induced settlement

当已知某场地是否发生液化，且能确定土体参数、地震参数、场地条件，则可以根据该模型进行推理，得到液化引起的沉降量，例如沉降量为严重(30～70 cm)的概率可由式(1)～式(3)计算得

式中：模型的所有变量的联合概率为

P(LH,LP,LPI,SP,EP,FC)=

P(SP)·P(FC)·P(EP|SP,FC)·P(LP|SP,EP,FC)×

P(LPI|LP,FC)·P(LH|SP,EP,FC,LP,LPI)

同时，该模型也可以根据场地的土体参数、地震参数和场地条件来预测液化发生的概率，可以表示为

2 地震液化沉降的评估模型建立

Hu等通过融合专家知识(解释结构模型)和数据学习(K2算法)的混合贝叶斯网络建模方法，建立了12个影响因素的地震液化贝叶斯网络预测模型，如图2所示。

本文基于该模型，考虑地基沉降的影响因素，如地震峰值加速度、可液化土层的埋深和厚度以及土质类别等[15]，另外加入Iwasaki等[16]提出的液化潜能指数，用来描述场地液化的程度，采用Hu等的建模方法：首先基于领域知识，利用解释结构模型方法建立一个具有结构层次的初始贝叶斯网络模型，然后结合K2结构学习算法，使其能融合初始模型中的领域知识(变量之间的关系和排序及其父节点的最大个数)和结构学习中的数据信息，进行混合学习，从而建立地震液化沉降的贝叶斯网络评估模型，如图3所示。

图2 地震液化的贝叶斯网络预测模型Fig.2 A Bayesian network for predicting seismic liquefaction

图3 地震液化沉降的贝叶斯网络评估模型Fig.3 A Bayesian network for assessing seismic liquefaction-induced settlement

人工神经网络是由大量神经元以某种链接方式形成的映射模型，一般可分为输入层、隐含层和输出层。常见的人工神经网络模型是采用RBF和多层感知器(Multi-layer Perceptron, MLP)进行信息的处理，其中MLP模型通常采用BP(Back Propagation)算法，其收敛速度、逼近能力和分类能力都比RBF神经网络模型的要差，因此本文采用RBF神经网络模型进行学习并建立地震液化沉降的评估模型，如图4所示。该模型采用人工多次调整隐含层数来进行模型的训练学习，最终确定模型学习精度最大所对应的隐含层数为20层。

此外，在地基沉降的简化计算法中，I & Y法进行地震液化沉降风险评估比Tokimatsu & Seed法要偏于安全。因此，本文将采用I & Y法对收集的液化地基沉降数据进行评估。I & Y法的基本原理是将场地条件和地震强度信息结合土体的标准贯入锤击数转化为土层液化安全系数，建立砂质土的相对密度-液化安全系数-土层体积应变之间的关系，然后分别计算每层土的体积应变，进而得出地基的总沉降量。其具体计算过程可以参考Ishihara等的研究。

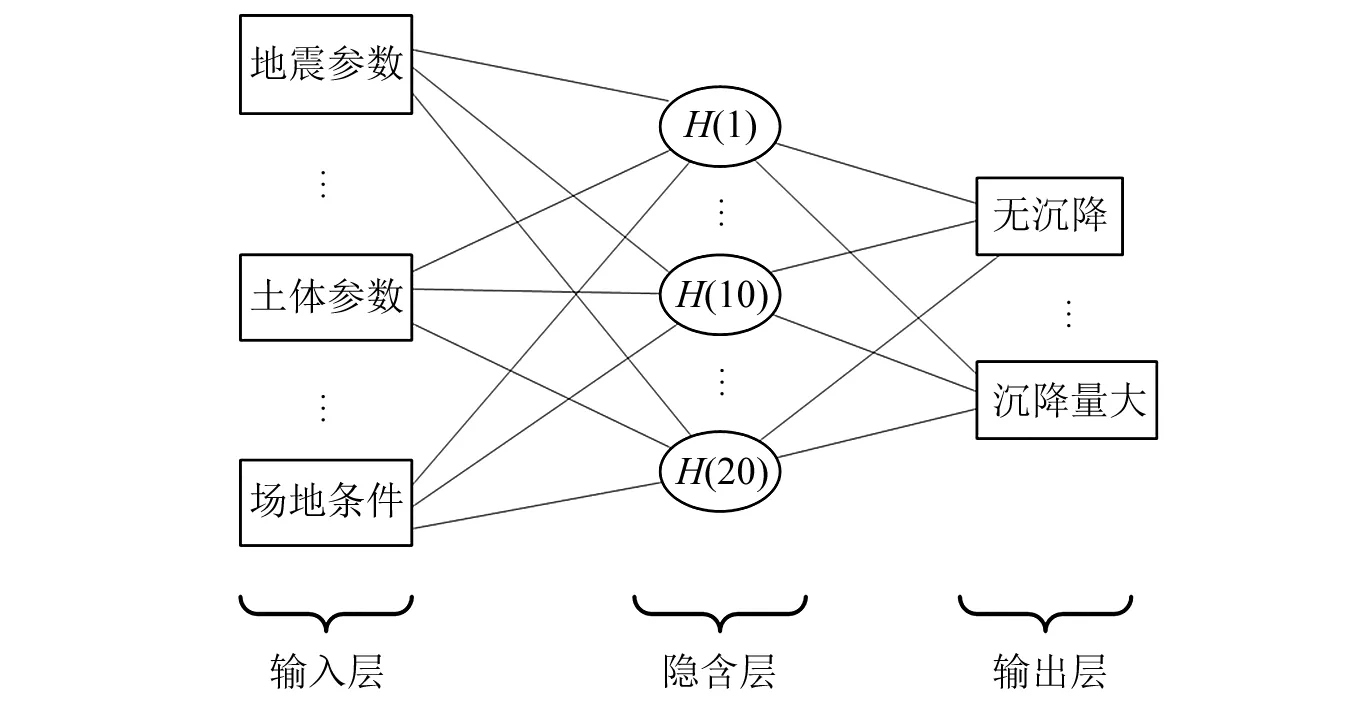
图4 地震液化沉降的神经网络评估模型Fig.4 A neural network for assessing seismic liquefaction-induced settlement

3 算 例

3.1 地震液化沉降数据

本文收集了442组现场标贯试验(Standard Penetration Test, SPT)点的地震液化沉降数据，包括245个液化场地和197个未液化场地。随机抽取332组沉降数据(184组液化样本和148组未液化样本)作为训练样本，剩余的110组作为验证样本。由于液化灾害数据中存在部分数据缺失现象，如平均粒径的缺失比例为15.2%，上覆有效应力的缺失比例为29.4%，数据缺失比例最大的变量是可液化层厚度，高达38.9%，因此采用适合缺失数据学习的期望值最大化算法(Expectation Maximization, EM)进行参数学习，获得贝叶斯网络模型中变量的条件概率。所有地震液化沉降灾害数据分别来源于1999年我国里氏7.6级台湾集集地震[17](http:∥cecas.clemson.edu/chichi/TW-LIQ/Homepage.html)，1957年美国5.3级California Daly地震以及1987年5.9级Whittier Narrows地震[18]，2011年日本东北地区太平洋近海岸9.0级地震。液化的12个影响因素的等级划分说明可参见Hu等的研究，剩余的两个影响参数，液化潜能指数和地基沉降是根据已有的研究成果划分等级标准，如表1所示。例如，液化后潜能指数根据Iwasaki等的建议分为4个等级来反映场地的不同液化程度。由于大多时候，工程师们只需要对液化场地的地基沉降进行大致评估，因此地基沉降量可以根据Ishihara等的研究划分为4个等级来反映其灾害的不同严重程度，其中将0.3

表1 部分参数的等级划分

3.2 模型性能的评估指标

模型性能的评估指标中最常用的是总体精度(OA)它反映了模型的整体预测性能，是预测准确的样本量占总样本量的比例。除这个指标外，作为信息检索分类中常用的两个指标，准确率(Pre)和召回率(Rec)被用来反映模型预测时某一分类中预测正确的概率，其中准确率也叫做查准率，表示模型预测正确的某一类样本量占模型预测为该类样本的总数的比例，召回率也叫做查全率，是模型预测正确的某一类样本量占该类真实样本量的比例。在地震液化预测中，理想情况下是希望模型的准确率和召回率都高，既能完美地区分哪些是液化样本，哪些是非液化样本，又能做出百分之百对的预测，但是Pre和Rec是相互制约的，一般情况下准确率高时，召回率就相对较低，因此需要找到一个融合准确率和召回率的指标。F1就是一个准确率和召回率的平均调和指标，用来综合反映模型的分类预测效果，当F1较高时，说明准确率和召回率都相对较高，则模型的预测效果很好。F1的计算公式为

F1=2·Pre·Rec/(Pre+Rec)

(4)

此外，一个性能好的模型除了要有较高的预测准确率外，还需要有较好的可靠性或有效性。受试者工作特征曲线(OC)曲线下面积(AUC)和Brier评分可以很好地反映模型的可靠性，其中ROC是以假阳性率(模型预测假样本的错误数量占假样本量的比例)为横轴，真阳性率(也就是召回率)为纵轴所绘制的曲线图，其曲线下面积AUC的值一般介于0.5～1.0，AUC的值越大，模型的预测性能越好。而Brier评分用于评估模型的预测均方概率误差，由Brier[19]在1950年提出，其表达式为

(5)

3.3 地基沉降的评估结果分析与讨论

基于贝叶斯网络、RBF神经网络和I & Y法的110组地基沉降的评估结果，如表2所示。

表2 不同液化沉降模型的评估结果对比

其中I & Y法计算的液化沉降为一个具体值，图5为该方法计算得到的某一个场地地基液化沉降量，而贝叶斯网络方法和神经网络方法计算的液化沉降是其某一个分类范围的概率值。首先对比预测精度(OA)和Brier评分值(B)两个指标，BN模型的预测精度最好，Brier评分值最小，而I & Y法的预测精度最差，且I & Y法没有Brier评分值，这是因为I & Y法是确定性评估方法，无法计算Brier评分值。因此，从模型的整体评估性能上来看，BN模型的评估结果最可靠。进一步分析沉降各分类中的评估指标F1和AUC，可以发现BN模型的各沉降类别的F1值和AUC值几乎都是比其他两种方法要大。因此，综合各评估指标的计算结果，BN模型无论是模型的整体评估可靠性还是各分类沉降量的预测性能都最好，说明了本文液化沉降的贝叶斯网络评估模型是准确有效的。此外，在I & Y法的评估结果，可知，该方法在评估中大沉降量和无沉降发生这两种情况时，其计算准确性较好，但对小沉降量的评估能力较差。

图5 日本东北地区太平洋近海岸地震中场地编号CH022勘测点的地震液化沉降计算结果Fig. 5 Calculation result of seismic liquefaction-induced settlement of a site No. CH022 in the Pacific coast of Tohoku earthquake

为了进一步说明贝叶斯网络模型在液化沉降评估中的优势，下面对液化沉降的发生进行因果推理和诊断推理。表3为液化沉降的贝叶斯网络模型中变量在不同先验已知情况下的后验概率，用来表示贝叶斯网络的因果推理过程。从表3可知，地震参数、土体参数和场地条件未知的情况下，“概率1”中液化的发生、LPI和沉降量的4种类别之间的概率值都相差不大，无法对场地的沉降灾害进行评估，而当已知地震参数、土体参数和场地条件时，可根据该模型进行推理知道场地发生液化的概率是多少。如果预测为液化，则可以将液化的等级“是”可改变该概率值为100%，那么LPI和沉降量的4种类别之间的概率值都会发生变化，从“概率2”中可知场地最可能出现中等程度液化，沉降量大。如果进一步将LPI的中等液化概率值改为100%，则最后推理出场地发生严重沉降量的可能性最大。在整个贝叶斯网络推理过程中，已知的场地地基液化相关的信息量越多，各变量的先验概率的准确性越高，推理的结果越准确，且推理过程中的因果关系越符合液化沉降的发生机制。

该贝叶斯网络模型处理上述推理分析能力外，还有逆向推理功能，如图6所示(采用Netica软件计算http:∥www.norsys.com/download.html)。如果知道某个场地发生了严重的沉降灾害，那么什么样的场地条件在什么样的地震作用下最可能导致该结果，这个就是概率论中的“最大可能解释”。从图6可知，地震等级“超大”、震中距“适中”、持续时间“适中”、地表峰值加速度“很高”、含“适当”细粒含量的“松散”砂土且其粒径“适中”、场地中土层“薄”且埋深“浅”、水位埋藏“浅”等，这样的情况下场地更容易发生液化，且液化后引起的沉降量会很大，这一结论符合目前对液化沉降的规律认知。模型的逆向推理能力有助于工程师们根据场地的抗震设防要求，预先评估能造成该场地某种程度灾害的最可能条件，为抗震设计提供科学依据。

表3 贝叶斯网络模型中部分变量的后验概率

图6 地震液化引起沉降的最大可能解释Fig. 6 The most probable explanation of seismic liquefaction-induced settlement

尽管贝叶斯网络和人工神经网络都是监督式学习方法，但贝叶斯网络是一种生成学习模型，模型中的每个节点代表一个随机变量，都具有其实际含义，节点和节点之间的连线表示因果关系，可以通过概率理论公式进行计算，从而对推理结果进行解释，而神经网络是一种判别式模型，模型中的每个节点不是随机变量，难以解释其实际含义，特别是其没有完备的理论基础，隐含层像一个“黑匣子”，节点之间是通过权重连接。更值得注意的是，贝叶斯网络方法可以向前、向后推理，例如可以通过输入地震相关参数、土体参数和场地条件预测场地是否液化，并进一步再评估场地的沉降量范围(见表3)，也可以通过已知场地的地基液化沉降量大小，反向推断什么样的地震、土体和场地条件最可能导致该沉降量(见图6)，而神经网络模型无法进行反向推理。另外，I & Y法是采用单元体试样的最大剪应变作为试样液化后排水体变的表征指标，建立了基于液化潜能指数的粗略估算方法。在液化潜能指数的计算中，该方法是根据地震强度的相关信息，如PGA(Peak Ground Acceleration)结合标准贯入锤击数进行转换计算，在这个转换计算中会使用一些经验系数和经验公式，这必然会造成估算结果上的差异。而且，对于长时间的地震作用下的地基液化沉降问题中，饱和砂土的沉降会持续增长，并不会受最大剪应力的明显限制[20]，这说明I & Y法会显著低估液化后土体的排水体变。而本文采用的贝叶斯网络方法综合考虑了地震液化沉降的多个影响因素，将这些因素以因果关系连接到场地的最终沉降值(包括液化后排水引起的沉降)上，通过概率计算进行沉降灾害评估。虽然本文的贝叶斯网络方法中也有液化潜能指数这一指标，但贝叶斯网络方法并不是像I & Y法那样单一采用“相对密度-液化安全系数-土层体积应变”一一对应的关系，而是综合考虑了地震强度参数、场地条件和土体性质来进行概率推理评估。

表4 地震液化沉降的因素敏感性分析

3.4 地基液化沉降的因素敏感性分析

地基发生液化沉降的原因相当复杂，影响因素也很多。表4给出了贝叶斯网络模型和神经网络模型的地震液化沉降影响因素的敏感性分析结果，为了便于对比分析，将两个模型的敏感性计算结果进行了标准化。在两个模型的沉降敏感分析结果中，贡献率(相对重要性)较大的前3个因素一致，分别为PGA、地震持续时间和标准贯入锤击数，这和沉降的简化算法中通过标准贯入锤击数结合地震强度信息估算土层竖向应变的原理中考虑的参数一样，不同的是本文的机器学习模型还综合考虑了其他一些重要的因素，如上浮有效应力、土层的埋深和厚度等，可对高度非线性和不确定性的液化沉降评估进行概率推理分析，因此机器学习模型的评估可靠性更强。本文的贝叶斯网络模型可先通过综合考虑地震强度相关参数、场地条件和土体的性质参数进行场地液化的概率预测，然后再结合场地是否液化和液化潜能指数及沉降的重要影响参数(如PGA、持续时间和标准贯入锤击数等)进行进一步概率推理，并评估沉降量，但该模型无法反映地震液化土因排水固结引起的地基沉降这一机制。这有待进一步进行研究，探讨数学模型与物理机理的融合问题，从而使模型可以反映液化沉降的机制。

4 结 论

本文综合考虑了多个地震参数、场地条件和土体参数，分别基于贝叶斯网络方法和径向基神经网络方法建立了地震液化沉降的评估模型，并与传统的I & Y简化计算方法进行了对比，其中地震液化沉降的贝叶斯网络模型的评估性能最好，而I & Y简化方法评估性能最差。所建立地震液化沉降的贝叶斯网络模型能很好地处理地基沉降的影响因素间的非线性关系和不确定性问题，其不仅可以预测液化的发生概率，还可以进一步评估场地的沉降灾害大小，而且该模型能进行逆向因果推理，评估场地和土体条件已知的情况下什么样的地震条件最可能导致该沉降灾害结果。此外，通过机器学习模型的敏感分析发现PGA、地震持续时间和标准贯入锤击数为较敏感因素，和简化算法考虑的参数基本一致。