机匣-双转子高维系统建模与实验验证

孙传宗， 杨 瑞， 陈予恕， 侯 磊,2

(1.哈尔滨工业大学 航天学院，哈尔滨 150001； 2. 哈尔滨工业大学 能源科学与工程学院，哈尔滨 150001)

现代航空发动机对高推重比的需求使得系统结构刚度不断降低，转静子振动耦合问题日益突出[1]。转子模型是否被准确建立、机匣及基础支承的刚度和质量是否被合理引入，将影响系统临界转速、转子动力学响应计算结果的有效性和精度。虽然可以采用支承动刚度代替机匣及支承的影响，但在临界转速附近振动响应的求解不够准确，同时无论采用测试或是数值仿真，都较难获得发动机各个支点准确的动刚度值[2]。避免上述问题的途径之一是采用整机动力学建模方法，将支承动刚度转化为内力平衡条件，从而避开支承刚度及质量合理取值的问题。

针对航空发动机整机振动，国内外学者开展了大量的研究工作。苏民等[3-4]分别应用传递矩阵法建立了实际航空发动机的整机动力学模型，分析了临界转速及应变能分布。周海仑等[5-9]分别基于集总质量、离散梁单元或连续梁建立了包含碰摩、轴承非线性的整机耦合动力学模型，利用时域积分法系统地研究了响应特征并进行了实验验证。Schönrock等[10-11]分别应用有限元软件建立了航空发动机整机有限元模型，研究了风扇叶片脱落以及发动机受导弹冲击过程的响应特征。为提高计算效率，一般采用模态综合法实现模型维度的减缩。Glasgow等[12]将固定界面模态综合法应用到转子系统的动力特性分析中。张文[13]基于模态综合法讨论了转子系统进动回转、不平衡响应和运动稳定性等问题。杨喜关等[14]利用固定界面模态综合法建立了反向旋转双转子动力学模型，研究了加速时域特性、进动转速变化特性及内外转子盘质心变化规律。Zuo等[15-17]分别研究了将改进模态综合法或混合界面模态综合法应用于转子-支承-机匣模型中的算法和流程。然而在已有文献中，无论是传递矩阵法还是有限元法中的梁单元，都无法满足复杂结构转子系统精确分析的需要，实体有限元模型也因建模复杂性和求解时效问题，鲜有针对复杂结构转子系统开展的动力学研究。

本文以某航空发动机缩比实验台为研究对象，借助商业有限元软件ANSYS建立了高精度的机匣-双转子实体有限元模型，将Craig-Bampton模态综合法[18]应用到高维模型的缩减计算中，实现了转子和机匣子结构的维度缩减与整机动力学模型组装，利用临界转速和振型验证了缩减模型的有效性和计算精度。在此基础上，进行了整机动力学求解和分析，并通过实验测试对本文建立的模型进行了验证。

1 实验台结构及有限元建模

1.1 机匣-双转子实验台结构

图1所示的航空发动机双转子缩比实验台隶属于哈尔滨工业大学ADVC实验室，该实验台采用了结构相似性设计方法，在保留实际航空发动机机匣、叶片和安装节支承等主要特征的基础上，将多级压气机盘(和涡轮盘)等效为单级叶盘结构，叶片简化为斜切平板结构。机匣采用可表征多级涵道和真机传力路径的三层壳体结构设计、制造和安装。低压转子系统采用1-0-1支承形式，以串联在低压压气机端的调速电主轴电机执行驱动；高压转子系统采用0-1-1支承形式，采用调速电主轴电机和圆锥齿轮机构实现驱动。该实验台能够有效性模拟多盘不平衡、单点和/或全周碰摩、转轴不对中等常见故障。

图1 机匣-双转子实验台Fig.1 Casing-dual-rotor test rig

1.2 机匣-双转子实验台有限元模型

为准确反映机匣-双转子实验台的动力学响应，采用有限元实体单元法建立仿真模型[19]。针对实验台的结构特点，确定建模方案步骤如下：

步骤1按照低压转子子系统、高压转子子系统、机匣子系统划分系统组成，将各个子系统等效化简为由单一结构件表示。

步骤2在保证质量分布和刚度分布与实际结构相似的条件下，忽略小圆孔、倒圆角等细小特征。采用等效刚性环方法建立压气机叶片和涡轮盘叶片模型。

步骤3应用8节点6面体单元剖分并建立低压转子、高压转子和机匣三维有限元模型。在轴承中心点和轮盘中心点建立虚节点，通过无质量刚性梁单元连接虚节点与相应连接区域节点。

步骤4轴承和安装节支承看作为线弹性支承，在ANSYS中以Combine 14单元建立。连接相应虚节点完成机匣-双转子模型组装。

根据以上方案建立的实验台有限元模型共计59 094个单元，103 616个节点。其中低压转子模型为8 820个单元，13 455个节点；高压转子模型为5 715个单元，8 640个节点；机匣模型为43 476个单元，81 500个节点，有限元模型如图2所示。

图2 机匣-双转子实验台有限元模型Fig.2 FE model of casing-dual-rotor test rig

2 模型自由度缩减及综合

基于实体单元建立的有限元模型往往结构复杂、自由度多、计算量大，在实际应用中受到限制。为此，本文基于Craig-Bampton模态综合法对系统进行维度缩减。针对实验台的结构特点，将其划分为高压转子模型、低压转子模型和机匣模型分别考虑。一般情况下，上述模型的动力学方程[20]可以表述为

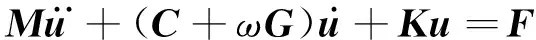
(1)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；G为陀螺矩阵；u为位移矢量；F为外力矢量；ω为转子转速。

考虑转子不平衡是引发系统振动的主要激励源，因此将轴承中心处虚节点和盘中心处虚节点看作为保留主节点，其余节点为从属节点划分方程式(1)。以主、从节点描述的动力学方程为

(2)

式中：Mmm，Mss，Cmm，Css，Gmm，Gss，Kmm，Kss分别为对应主节点和从属节点的质量、阻尼、陀螺和刚度矩阵；Mms，Msm，Cms，Csm，Gms，Gsm，Kms，Ksm分别为主、从节点耦合的质量、阻尼、陀螺和刚度矩阵；um，us分别为主、从节点位移矢量；Fm为主节点外力矢量。

将系统运动看作为约束界面保留主模态和全部界面自由度的约束模态组成，则

(3)

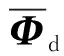
(4)

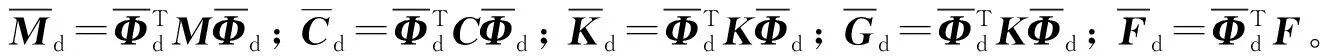
式(4)描述的动力学方程极大地缩减了原高维模型的计算维度，高压转子模型、低压转子模型和机匣模型均可以按照式(4)分别缩减为很低自由度的分析模型，则整机动力学模型可以根据边界协调条件，将若干子模型相耦合得到。实际应用中，借助ANSYS子结构求解模块CMS，利用APDL语言和C#程序完成高维实体有限元模型的维度缩减与矩阵提取，实施流程图如图3所示。

图3 机匣-双转子模型缩减过程流程图Fig.3 Flow chart of the reducing process for casing-dual-rotor model

3 数值仿真分析

3.1 计算模型及参数

模态截断频率对计算精度有较大的影响，这里按照文献[21]设定保留模态频率不低于系统最大工作转速的2倍。机匣-双转子实体有限元模型经过缩减后得到仅包含58个自由度的低维模型，其中低压转子模型由8个位移坐标和10个保留模态坐标组成，高压转子模型由10个位移坐标和8个保留模态坐标组成，机匣模型由14个位移坐标和8个保留模态坐标组成。

轴承等效刚度通过文献[22]中表2-1计算得到，安装节刚度通过仿真计算得到。支承参数值见表1；安装节位置如图4所示。

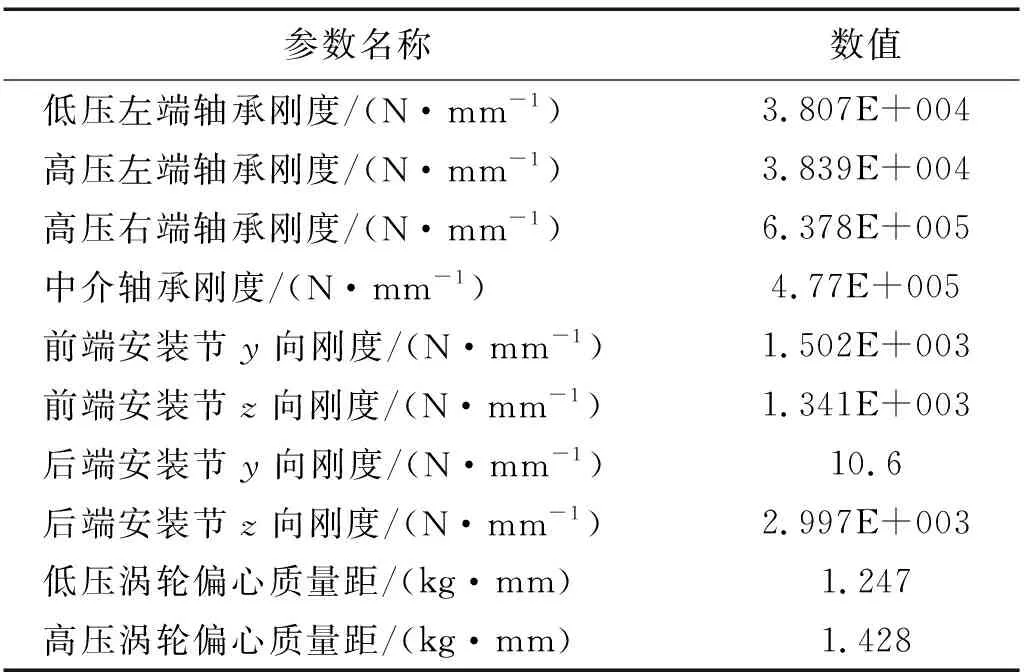
表1 机匣-双转子实验台支承参数

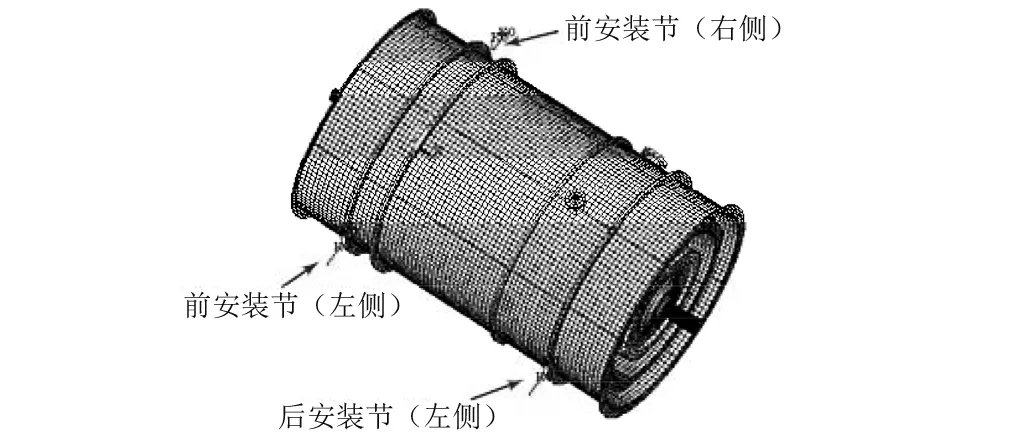
图4 安装节支承示意图Fig.4 Schematic diagram for mount supportings

3.2 临界转速和振型计算及验证

由动力学方程计算双转子系统临界转速的方法如下：计算多种自转转速下的系统共振频率，绘制转子系统Campbell图，利用自转频率和共振频率相等关系，获取系统临界转速，借助转子自转方向判断转子涡动方向[23]。计算时，设定高/低压转子为同向旋转，转速比取1.2。

表2为分别由ANSYS和本文方法计算得到的前3阶临界转速值。由表2可知，缩减模型具有很高的计算精度，与实体有限元结果相比，前3阶临界转速最大偏差未超过0.8%。

表2 机匣-双转子系统临界转速

由于高压主激励振型与低压主激励振型相近，这里仅给出以低压转子为主激励的临界转速振型，如图5和图6所示。由图5～图6可知，缩减模型结果与有限元模型结果也呈现出高度的一致性。

综合临界转速数值和振型对比结果可以得出，由本文方法得到的低维缩减模型能够精确反映原复杂高维模型主要关注点的动力学特征，该模型具有高精度和低维度优势。

图5 ANSYS中得到的前3阶临界转速振型Fig.5 The first three orders critical mode in ANSYS

图6 MATLAB中得到的前3阶临界转速振型Fig.6 The first three orders critical speed mode in MATLAB

3.3 基于双转子缩减模型的振动响应分析

以1.2转速比为例，利用Runge-Kutta时域积分法求解得到机匣-双转子缩减模型的动力学响应。图7给出了低压压气机中心节点的三维频谱图。从图7可知，该节点在x和y方向上的幅值呈现出较大的差异性，如x方向的高压同步频率幅值有3个显著峰值，分别对应低压转速为 145.0 rad/s，369.0 rad/s和561.0 rad/s，而在y方向仅有2个明显的峰值，分别对应低压转速 129.0 rad/s和529.0 rad/s；x方向的低压同步频率幅值在总幅值中占有较高比重，而在y方向仅占有相对较小的比重。图8给出了低压转速为529.0 rad/s时，低压压气机中心节点的轴心轨迹图，从图8可知，有明显的倾覆现象，根据动力学理论可以推断出，机匣安装节的非对称刚度是导致上述现象的主要原因，这将影响转子系统的检测与识别。

图7 低压压气机中心点的三维频谱图Fig.7 3D spectrogram of lower pressure disc center

图8 低压压气机中心点轴心轨迹 (ωlow=529.0 rad/s)Fig.8 Whirl orbit of lower pressure disc center (ωlow=529.0 rad/s)

4 振动响应实验验证

采用模态实验和振动响应实验校验本文模型的有效性，其中模态实验通过锤击法实现；振动响应实验通过电涡流传感器测量低压涡轮盘振动位移获得系统响应信息。主要仪器包括Dewetron-801数据采集系统，ZA210504型高精度电涡流传感器和Kistler力锤，实验器实物图，如图9所示。

图9 振动实验实物图Fig.9 Vibration test of test rig

图10为利用锤击法测得的实验台频率响应曲线，表3给出了实验模态和仿真模态的比较。对比分析表3中数据可知，在主要的低阶频率范围内，各阶仿真模态数值与实验模态数值吻合度很好，仅在第4阶模态频率出现一定差距。

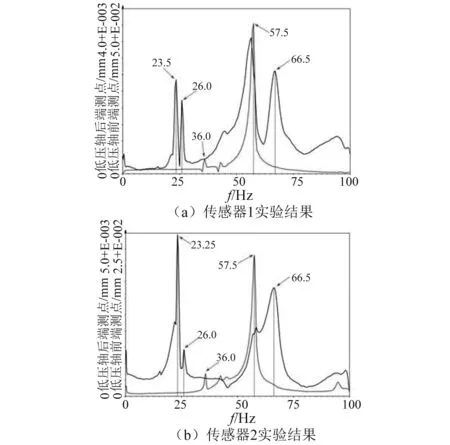
图10 锤击实验得到的频响函数Fig.10 Frequency response function by hammer

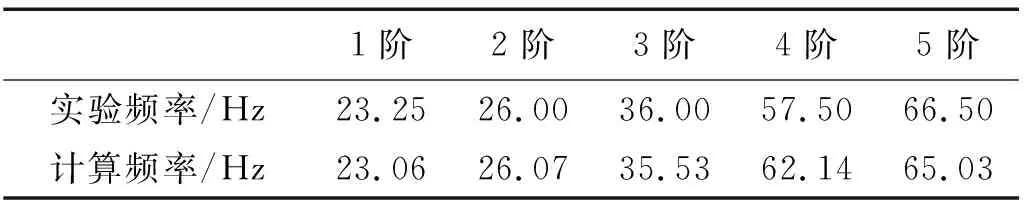
1阶2阶3阶4阶5阶实验频率/Hz23.2526.0036.0057.5066.50计算频率/Hz23.0626.0735.5362.1465.03

分别通过试验测试和数值仿真获得低压转速ωl≈2 710 rad/s，高压转速ωh≈2 870 rad/s时，低压涡轮中心点的轴心轨迹、x方向时域响应和频域响应谱，如图11和图12所示。可见数值仿真结果与试验测试结果吻合度较好，仿真结果较好地反映了由非对称支承刚度导致的“菱形”轴心轨迹，从图11和图12可知，高压和低压转速接近时出现的拍振现象。

图11 由仿真计算得到的低压涡轮中心点振动响应Fig.11 Vibration responses of lower turbine center under numerical calculation

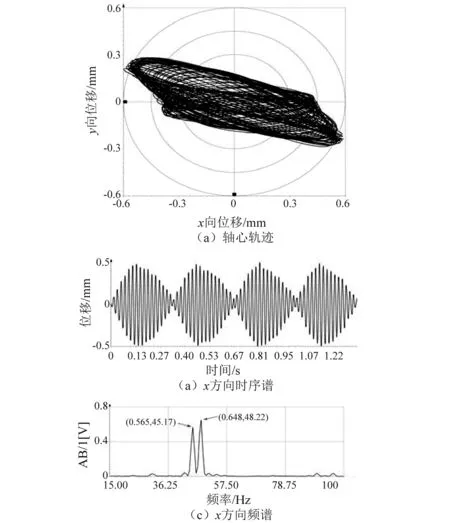
图12 由实验测试得到的低压涡轮中心点振动响应Fig.12 Vibration responses of lower turbine center under experimental test

5 结 论

本文以某机匣-双转子实验台为研究对象，研究了一类包含机匣和安装节支承双转子系统的精确化建模和维度缩减问题，主要结论如下：

(1) 基于Craig-Bampton模态综合理论，并借助商业有限元软件成功地将机匣-双转子复杂高维实体有限元模型缩减至仅包含数10个自由度的极低维模型，同时保持很高的计算精度。

(2) 研究发现受机匣安装节非对称支承影响，系统的频谱响应在水平方向和竖直方向表现出较大的差异，轴心轨迹与对称转子系统结果也有显著不同，这将影响对转子系统振动响应的检测与识别。

(3) 进行了模态实验和振动响应实验，通过与数值结果比较，结果达到了较好的一致性，在一定程度上表明本文所建立的模型准确、有效。

目前，实验主要集中在模态试验和定性的振动响应验证方面，初步检验了本文所建模型的有效性。限于篇幅，关于全转速域下系统动力学响应的对比校验，以及包含轴承非线性模型和转子动平衡测试等工作将在后续研究中深入开展。